Câu hỏi 1 :
Điện trường trong khí quyển gần mặt đất có cường độ 200 V/m, hướng thẳng đứng từ trên xuống dưới. Một electron (-e = -1,6.10-19 C) ở trong điện trường này sẽ chịu tác dụng một lực điện có cường độ và hướng như thế nào?
- A
3,2.10-21 N; hướng thẳng đứng từ trên xuống
- B
3,2.10-17 N; hướng thẳng đứng từ trên xuống
- C
3,2.10-21 N; hướng thẳng đứng từ dưới lên
- D
3,2.10-17 N; hướng thẳng đứng từ dưới lên
Đáp án: D
Lời giải chi tiết:
Ta có: \(F = qE = 1,{6.10^{ - 19}}.200 = 3,{2.10^{ - 17}}N\)
Do electron mang điện tích âm nên \(\overrightarrow F \uparrow \downarrow \overrightarrow E \) => \(\overrightarrow F \) hướng thẳng đứng từ dưới lên.
Câu hỏi 2 :
Lực điện trường tác dụng lên điện tích điểm có phương
- A
Trùng với đường sức
- B
Song song với đường sức
- C
Tiếp tuyến với đường sức
- D
Tạo với đường sức góc bất kì
Đáp án: C
Phương pháp giải:
Vận dụng lí thuyết về lực điện và chuyển động của electron trong điện trường
Lời giải chi tiết:
Lực điện trường tác dụng lên điện tích điểm có phương tiếp tuyến với đường sức
Câu hỏi 3 :
Hai điện tích \({q_1} = - q;{q_2} = 4q\) đặt cách nhau một khoảng r. Nếu điện tích \({q_1}\) tác dụng lực điện lên điện tích \({q_2}\) có độ lớn là F thì lực tác dụng của điện tích \({q_2}\) lên \({q_1}\) có độ lớn là:
- A
F.
- B
4F.
- C
2F.
- D
0,5F.
Đáp án: A
Phương pháp giải:
Áp dụng định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Lời giải chi tiết:
Theo định luật Cu-lông ta có: Lực tác dụng của điện tích \({q_1}\) lên \({q_2}\) và lực tác dụng của điện tích \({q_2}\) lên \({q_1}\) bằng nhau: \({F_{12}} = {F_{21}} = F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Câu hỏi 4 :
Trong trường hợp nào sau đây ta có một tụ điện?
- A
hai tấm gỗ khô đặt cách nhau một khoảng trong không khí.
- B
hai tấm nhôm đặt cách nhau một khoảng trong nước nguyên chất.
- C
hai tấm kẽm ngâm trong dung dịch axit.
- D
hai tấm nhựa phủ ngoài một lá nhôm.
Đáp án: B
Lời giải chi tiết:
Ta có: Tụ điện là hệ 2 vật dẫn đặt gần nhau nhưng không tiếp xúc với nhau được ngăn cách nhau bằng một môi trường cách điện
Lại có, nước nguyên chất không dẫn điện, nhôm là vật dẫn nên phương án B: hai tấm nhôm đặt cách nhau một khoảng trong nước nguyên chất được coi như một tụ điện.
Câu hỏi 5 :
Hai thành phần mang điện trong nguyên tử là:
- A
Electron mang điện tích dương và hạt nhân mang điện tích âm
- B
Hạt nhân và electron mang điện tích âm
- C
Hạt nhân mang điện tích dương và electron mang điện tích âm
- D
Hạt nhân và electron mang điện tích dương
Đáp án: C
Lời giải chi tiết:
Ta có, mọi nguyên tử gồm có:
- Hạt nhân ở trung tâm mang điện tích dương, notrơn không mang điện
- Lớp vỏ các electron mang điện tích âm, chuyển động xung quanh hạt nhân.
Câu hỏi 6 :
Một tụ điện phẳng có điện dung C = 200pF được tích điện đến hiệu điện thế U = 4 V. Khoảng cách giữa hai bản tụ điện là d = 0,2 mm. Điện tích của tụ điện là:
- A
\({5.10^{ - 10}}C\)
- B
\({8.10^{ - 10}}C\)
- C
\({8.10^{ 10}}C\)
- D
\({0,8.10^{ - 10}}C\)
Đáp án: B
Lời giải chi tiết:
Điện tích của tụ điện là:
\(Q = CU = {200.10^{ - 12}}.4 = {8.10^{ - 10}}C\)
Câu hỏi 7 :
Tại một điểm trong không khí có hai cường độ điện trường có phương vuông góc với nhau và có độ lớn lần lượt là E1 = 6.104 V/m; E2 = 8.104 V/m. Độ lớn của điện trường tổng là:
- A
10.104 V/m
- B
14.104 V/m
- C
2. 104 V/m
- D
48.104 V/m
Đáp án: A
Lời giải chi tiết:
Độ lớn điện trường tổng hợp là:
\(E = \sqrt {E_1^2 + E_2^2} = \sqrt {{{\left( {{{6.10}^4}} \right)}^2} + {{\left( {{{8.10}^4}} \right)}^2}} = {10.10^4}V/m\)
Câu hỏi 8 :
Có mấy loại điện tích:
- A
1
- B
2
- C
3
- D
4
Đáp án: B
Lời giải chi tiết:
Có loại điện tích là: điện tích âm và điện tích dương
Câu hỏi 9 :
Có bốn vật $A, B, C, D$ kích thước nhỏ, nhiễm điện. Biết rằng vật $A$ hút vật $B$ nhưng lại đẩy $C$. Vật $C$ hút vật $D$. Khẳng định nào sau đây là sai.
- A
Điện tích của vật $A$ và $D$ trái dấu.
- B
Điện tích của vật $A$ và $D$ cùng dấu.
- C
Điện tích của vật $B$ và $D$ cùng dấu.
- D
Điện tích của vật $A$ và $C$ cùng dấu.
Đáp án: B
Lời giải chi tiết:
Ta có:
+ Lực tương tác giữa 2 điện tích là là lực đẩy khi q1.q2 > 0
+ Lực tương tác giữa 2 điện tích là lực hút khi q1.q2 < 0
Theo đầu bài, ta có:
+ A hút B => qA.qB < 0
+ A đẩy C => qA.qC > 0
+ C hút D => qC.qD < 0
=> A và C cùng dấu, B và D cùng dấu, A và D khác dấu
Câu hỏi 10 :
Biểu thức nào sau đây xác định thế năng của một điện tích điểm q tại điểm M trong điện trường?
- A
WM = AM∞ = qVM
- B
WM = AM∞ = VM/q
- C
WM = AM = VM
- D
WM = AM∞ = q/VM
Đáp án: A
Lời giải chi tiết:
Thế năng của một điện tích điểm q tại điểm M trong điện trường: WM = AM∞ = qVM
Câu hỏi 11 :
Hai điện tích q1 và q2 đặt gần nhau trong chân không có lực tương tác là F. Nếu đặt điện tích q3 trên đường nối q1 và q2 và ở ngoài q2 thì lực tương tác giữa q1 và q2 là F’ có đặc điểm:
- A
F’ > F
- B
F’ < F
- C
F’ ≥ F
- D
Không phụ thuộc vào q3
Đáp án: D
Phương pháp giải:
Vận dụng biểu thức xác định lực tương tác giữa 2 điện tích đặt trong chân không: $F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}$
Lời giải chi tiết:
Ta có lực tương tác giữa hai điện tích q1 và q2 là:
$F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}$
=> Lực tương tác này không phụ thuộc vào q3
Câu hỏi 12 :
Gọi F là lực điện mà điện trường có cường độ điện trường E tác dụng lên một điện tích thử q . Nếu tăng q lên gấp đôi thì E và F thay đổi ntn ?
- A
Cả E và F đều tăng gấp đôi
- B
Cả E và F đều không đổi
- C
E tăng gấp đôi , F không đổi
- D
E không đổi , F tăng gấp đôi
Đáp án: D
Phương pháp giải:
+ Xem lí thuyết phần II
+ Áp dụng biểu thức tính lực điện: $F = k\frac{{\left| {qQ} \right|}}{{\varepsilon {r^2}}}$
Lời giải chi tiết:
Ta có,
+ Cường độ điện trường E không phụ thuộc vào điện tích thử q
+ Lực điện: $F = k\frac{{\left| {qQ} \right|}}{{\varepsilon {r^2}}}$
=> Khi q tăng lên gấp đôi thì, E không đổi và F tăng gấp đôi
Câu hỏi 13 :
Cho biết trong 22,4l khí hiđro ở 00 và dưới áp suất 1atm thì có 2.6,02.1023 nguyên tử hiđrô. Mỗi nguyên tử hiđrô gồm hai hạt mang điện là proton và electron. Tổng các điện tích dương và tổng các điện tích âm trong 1cm3 khí hiđrô là?
- A
8,6C và 8,6C
- B
17,2 C VÀ 4,3C
- C
8,6C và 17,2C
- D
4,3C và 4,3C
Đáp án: A
Phương pháp giải:
+ Vận dụng biểu thức tính số mol khí ở nhiệt độ t và áp suất p: $n = \frac{{pV}}{{RT}}$
+ Điện tích của electron: e = -1,6.10-19C
+ Điện tích của proton: 1,6.10-19C
Lời giải chi tiết:
Ta có:
+ 22,4 l khí hiđro ở 00 , p = 1atm tương ứng với 1mol khí hiđrô có số nguyên tử là 2.6,02.1023
+ Trong 1cm3 = 1ml = 10-3l sẽ có số nguyên tử là
\(N = \frac{{{{10}^{ - 3}}.2.6,{{02.10}^{23}}}}{{22,4}} = 5,{375.10^{19}}\) nguyên tử
Mỗi nguyên tử hiđrô có 1 electron và 1 proton
=> Số electron = số proton = 5,375.1019 hạt
Tổng các điện tích dương: Q = 5,375.1019.1,6.10-19 = 8,6C
Tổng các điện tích âm trong 1cm3 khí là: Q = 5,375.1019.|-1,6.10-19 | = 8,6C
Câu hỏi 14 :
Cho hai quả cầu nhỏ trung hòa điện đặt trong không khí, cách nhau 40 cm. Giả sử có 4.1012 electron từ quả cầu này di chuyển sang quả cầu kia. Tính độ lớn của lực tương tác giữa hai quả cầu đó. Cho biết điện tích của electron bằng - 1,6.10−19 C
- A 2,304.10-3N
- B 2,304.10-4N
- C 2,304.10-2N
- D 2,304.10-5N
Đáp án: C
Phương pháp giải:
Công thức tính lực tương tác: \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\)
Lời giải chi tiết:
Quả cầu mất electron sẽ nhiễm điện dương, quả cầu nhận electron sẽ nhiễm điện âm
Độ lớn của điện tích trên mỗi quả cầu :
\(\left| {{q}_{1}} \right|=\left| {{q}_{2}} \right|={{4.10}^{12}}.\left| -1,{{6.10}^{-19}} \right|=6,{{4.10}^{-7}}C\)
Lực tương tác giữa hai quả cầu:
\(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}={{9.10}^{9}}.\frac{{{\left( 6,{{4.10}^{-7}} \right)}^{2}}}{{{\left( {{40.10}^{-2}} \right)}^{2}}}=2,{{304.10}^{-2}}N\)
Câu hỏi 15 :
Khoảng cách giữa một proton và một electron trong một nguyên tử là \(5.10^{-9}cm\). Coi proton và electron là các điện tích điểm, lấy \(e = 1,6.10^{-19}C\). Lực tương tác điện giữa chúng là
- A
\(9,216.10^{-10}N\)
- B
\(9,216.10^{-11}N\)
- C
\(9,216.10^{-9}N\)
- D
\(9,216.10^{-8}N\)
Đáp án: D
Phương pháp giải:
Lực tương tác giữa hai điện tích điểm trong chân không có độ lớn \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Lời giải chi tiết:
Lực tương tác điện giữa electron và proton có độ lớn:\(F = k\dfrac{{{e^2}}}{{{r^2}}} = {9.10^9}.\dfrac{{{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{{{({{5.10}^{ - 11}})}^2}}} = 9,{216.10^{ - 8}}N\)
Câu hỏi 16 :
Hai quả cầu nhỏ giống hệt nhau bằng kim loại A và B đặt trong không khí, có điện tích lần lượt là q1 = -3,2.10-7 C, q2 = 2,4.10-7 C, cách nhau một khoảng 12 cm. Xác định số electron thừa và thiếu ở mỗi quả cầu?
- A Số electron thiếu ở quả cầu A là 2.1012 electron. Số electron thừa ở quả cầu B là 1,5.1012 electron
- B Số electron thừa ở quả cầu A là 1,5.1012 electron. Số electron thiếu ở quả cầu B là 2.1012 electron
- C Số electron thừa ở quả cầu A là 2.1012 electron. Số electron thiếu ở quả cầu B là 1,5.1012 electron
- D Số electron thiếu ở quả cầu A là 1,5.1012 electron. Số electron thừa ở quả cầu B là 2.1012 electron
Đáp án: C
Phương pháp giải:
Công thức tính điện tích: q = n.e
Lời giải chi tiết:
Số electron thừa ở quả cầu A là: \({n_A} = \left| {\frac{{{q_A}}}{e}} \right| = {2.10^{12}}\,\,\left( {electron} \right)\)
Số electron thiếu ở quả cầu B là: \({n_B} = \left| {\frac{{{q_B}}}{e}} \right| = 1,{5.10^{12}}\,\,\left( {electron} \right)\)
Câu hỏi 17 :
Cho hai điện tích \({q_1} = 1nC,{q_2} = 3nC\) đặt tại hai điểm \(AB\) cách nhau \(60cm\) trong chân không. Tìm điểm \(C\) mà cường độ điện trường tại đó có \(\overrightarrow {{E_1}} = - 3\overrightarrow {{E_2}} \)
- A
\(\left\{ \begin{array}{l}CA = 45cm\\CB = 15cm\end{array} \right.\)
- B
\(\left\{ \begin{array}{l}CA = 15cm\\CB = 45cm\end{array} \right.\)
- C
\(\left\{ \begin{array}{l}CA = 30cm\\CB = 90cm\end{array} \right.\)
- D
\(\left\{ \begin{array}{l}CA = 90cm\\CB = 30cm\end{array} \right.\)
Đáp án: B
Phương pháp giải:
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Lời giải chi tiết:
+ Gọi điểm cần tìm là \(C\) mà tại đó cường độ điện trường do \({q_1}\) và \({q_2}\) gây ra lần lượt là \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} \)
+ Theo đề bài ta có: \(\overrightarrow {{E_1}} = - 3\overrightarrow {{E_2}} \) (1)
Ta suy ra: \(\overrightarrow {{E_1}} \) cùng phương nhưng ngược chiều với \(\overrightarrow {{E_2}} \)
\( \Rightarrow \) \(C\) thuộc đường thẳng \(AB\).
+ Do \({q_1}\) và \({q_2}\) cùng dấu \( \Rightarrow C\) nằm trong đoạn \(AB\)
\( \Rightarrow CA + CB = AB = 60cm\) (2)
Từ (1), ta có:
\({E_1} = 3{E_2} \Leftrightarrow k\dfrac{{\left| {{q_1}} \right|}}{{C{A^2}}} = 3k\dfrac{{\left| {{q_2}} \right|}}{{C{B^2}}}\)
\( \Leftrightarrow \dfrac{{CB}}{{CA}} = \sqrt {3\dfrac{{\left| {{q_2}} \right|}}{{\left| {{q_1}} \right|}}} = \sqrt {3.\dfrac{{{{3.10}^{ - 9}}}}{{{{10}^{ - 9}}}}} = 3\) (3)
Từ (2) và (3) ta suy ra: \(\left\{ \begin{array}{l}CA = 15cm\\CB = 45cm\end{array} \right.\)
Câu hỏi 18 :
Hai điện tích điểm q1 = 4.10-6C; q2 = 36.10-6C đặt tại hai điểm cố đinh A và B trong dầu có hằng số điện môi ε = 2. AB = 16cm. Xác định vị trí của điểm M mà tại đó cường độ điện trường tổng hợp bằng không?
- A
MA = 4cm, MB = 12cm
- B
MA = 12cm, MB = 4cm
- C
MA = 8cm, MB = 8cm
- D
MA = 4cm, MB = 20cm
Đáp án: A
Phương pháp giải:
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Lời giải chi tiết:
Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} \)lần lượt là cường độ điện trường do q1 và q2 gây ra tại M.
Theo đề bài ta có:
\(\overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \to \overrightarrow {{E_1}} = \overrightarrow { - {E_2}} \to \overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \)=> M phải thuộc AB
Và vì 2 điện tích cùng dấu => M phải ở bên trong AB
Mặt khác: \(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon M{A^2}}}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon M{B^2}}}\end{array} \right. \to \frac{{{E_1}}}{{{E_2}}} = \frac{{\left| {{q_1}} \right|M{B^2}}}{{\left| {{q_2}} \right|M{A^2}}} = 1 \to \frac{{MA}}{{MB}} = \sqrt {\frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}} = \sqrt {\frac{{\left| {{{4.10}^{ - 6}}} \right|}}{{\left| {{{36.10}^{ - 6}}} \right|}}} = \frac{1}{3}\)
Lại có: MA + MB = 16
=> MA = 4cm, MB = 12cm
Câu hỏi 19 :
Điện tích \(q = {10^{ - 8}}\,\,C\) di chuyển dọc theo các cạnh của tam giác đều ABC cạnh \(a = 10\,\,cm\) trong điện trường đều cường độ điện trường là \(E = 300\,\,V/m\), \(\overrightarrow E //BC\). Tính công của lực điện trường khi \(q\) di chuyển trên mỗi cạnh của tam giác:
- A \({A_{AB}}\; = 1,{5.10^{ - 7}}J;{A_{BC}} = - {3.10^{ - 7}}J;{A_{AC}} = 1,{5.10^{ - 7}}J\)
- B \({A_{AB}}\; = 1,{5.10^{ - 7}}J;{A_{BC}} = {3.10^{ - 7}}J;{A_{AC}} = - 1,{5.10^{ - 7}}J\)
- C \({A_{AB}}\; = - 1,{5.10^{ - 7}}J;{A_{BC}} = {3.10^{ - 7}}J;{A_{AC}} = 1,{5.10^{ - 7}}J\)
- D \({A_{AB}}\; = - 1,{5.10^{ - 7}}J;{A_{BC}} = {3.10^{ - 7}}J;{A_{AC}} = - 1,{5.10^{ - 7}}J\)
Đáp án: C
Phương pháp giải:
Công của lực điện: \(A = qEd\)
Trong đó, d là hình chiếu của quỹ đạo lên phương của đường sức điện.
Lời giải chi tiết:
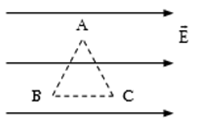
Công của lực điện trường khi q di chuyển trên cạnh AB là:
\({A_{AB}}\; = q.E.AB.cos{120^0} = {10^{ - 8}}.300.0,1.\left( { - 0,5} \right){\rm{ }} = - 1,{5.10^{ - 7}}\;J\)
Công của lực điện trường khi q di chuyển trên cạnh BC là:
\({A_{BC}}\; = q.E.BC = {10^{ - 8}}.300.0,1 = {3.10^{ - 7}}\;J\)
Công của lực điện trường khi q di chuyển trên cạnh AC là:
\({A_{AC}}\; = q.E.AC.cos60 = {10^{ - 8}}.300.0,1.0,5 = 1,{5.10^{ - 7}}\;J\)
Câu hỏi 20 :
Có 3 điện tích điểm q1 = 15.10-9C; q2 = -12.10-9C; q3 = 7.10-9C đặt tại ba đỉnh của tam giác đều ABC, cạnh 10cm. Điện thế tại tâm O và H - chân đường cao từ A xuống BC do ba điện tích gây ra là?
- A
V0 = 15,58V; VH = 658,8V
- B
V0 = 658,8V; VH = 658,8V
- C
V0 = 1558,8V; VH = 658,8V
- D
V0 = 658,8V; VH = 1658,8V
Đáp án: C
Phương pháp giải:
Áp dụng biểu thức tính điện thế: \({V_M} = \frac{{{A_{M\infty }}}}{q} = k\frac{Q}{r}\)
Câu hỏi 21 :
Tụ phẳng không khí được tích điện bằng nguồn điện có hiệu diện thế không đổi \(U\). Hỏi năng lượng của bộ tụ thay đổi thế nào nếu tăng khoảng cách \(d\) giữa hai bản tụ lên gấp đôi trong trường hợp vẫn nối tụ với nguồn?
- A
\({\rm{W}}' = 2W\)
- B
\({\rm{W}}' = {\rm{W}}\)
- C
\({\rm{W}}' = \dfrac{{\rm{W}}}{2}\)
- D
\({\rm{W}}' = 0\)
Đáp án: C
Phương pháp giải:
+ Vận dụng biểu thức tính điện dung của tụ điện phẳng: \(C = \dfrac{S}{{k.4\pi d}}\)
+ Vận dụng biểu thức tính năng lượng điện trường: \({\rm{W}} = \dfrac{1}{2}C{U^2}\)
Lời giải chi tiết:
Ta có:
+ Điện dung của tụ điện phẳng không khí là: \(C = \dfrac{S}{{k.4\pi d}}\)
+ Khi tăng \(d\) lên gấp đôi thì \(C\) giảm đi một nửa, khi đó \(C' = \dfrac{C}{2}\)
Khi tụ vẫn nối vào nguồn điện thì \(U\) không đổi và năng lượng ban đầu của tụ là \({\rm{W}} = \dfrac{1}{2}C{U^2}\)
Năng lượng của tụ khi tăng \(d\) là \({\rm{W}}' = \dfrac{1}{2}C'{U^2}\)
Vì \(C' = \dfrac{C}{2}\) nên \({\rm{W}}' = \dfrac{{\rm{W}}}{2}\)
Câu hỏi 22 :
Nối hai cực của nguồn điện không đổi có hiệu điện thế $50V$ lên hai bản của tụ điện phẳng có khoảng cách giữa hai bản tụ bằng $5cm$. Trong vùng không gian giữa hai bản tụ, $1$ proton có điện tích \(1,{6.10^{ - 19}}C\) và khối lượng \(1,{67.10^{ - 27}}kg\) chuyển động từ điểm M cách bản âm của tụ điện $4cm$ đến điểm N cách bản âm của tụ $1cm$. Biết tốc độ của proton tại M bằng \({10^5}m/s\). Tốc độ của proton tại N bằng:
- A
\(1,{25.10^5}m/s\)
- B
\(3,{57.10^5}m/s\)
- C
\(1,{73.10^5}m/s\)
- D
\(1,{57.10^6}m/s\)
Đáp án: A
Phương pháp giải:
+ Vận dụng biểu thức tính cường độ điện trường: \(E = \dfrac{U}{d}\)
+ Vận dụng biểu thức tính lực điện: \(F = qE\)
+ Áp dụng biểu thức định luật II - Newton: \(F = ma\)
+ Vận dụng biểu thức: \({v^2} - v_0^2 = 2{\rm{a}}s\)
Lời giải chi tiết:
Ta có:
+ Cường độ điện trường giữa hai bản tụ điện là:
\(E = \dfrac{U}{d} = \dfrac{{50}}{{0,05}} = 1000V/m\).
+ Lực điện trường tác dụng lên điện tích là \(F = qE = 1,{6.10^{ - 19}}.1000 = 1,{6.10^{ - 16}}N\).
+ Định luật II Niuton có \(F = ma\)
=> điện tích di chuyển trong điện trường với gia tốc \(a = \dfrac{F}{m} = \dfrac{{1,{{6.10}^{ - 16}}}}{{1,{{67.10}^{ - 27}}}} = 9,{58.10^{10}}m/{s^2}\)
\( \to v_N^2 - v_M^2 = 2as \Rightarrow {v_N} = \sqrt {2.9,{{58.10}^{10}}.0,03 + {{\left( {{{10}^5}} \right)}^2}} = 1,{25.10^5}m/s\).
Câu hỏi 23 :
Cho 4 điện tích \({q_{1\;}} = {q_{2\;}} = {q_{3\;}} = {q_4} = - {2.10^{ - 8}}C\) lần lượt đặt tại 4 đỉnh của hình vuông ABCD cạnh 4cm theo thứ tự A, B, C, D. Tìm lực điện tổng hợp tác dụng lên điện tích đặt tại D?
- A \(2,{31.10^{ - 3}}N\)
- B \(2,{06.10^{ - 3}}N\)
- C \(4,{06.10^{ - 3}}N\)
- D \(4,{31.10^{ - 3}}N\)
Đáp án: D
Phương pháp giải:
+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.
+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \)
+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.
Lời giải chi tiết:
Biểu diễn các lực tác dụng lên q4 như hình vẽ:
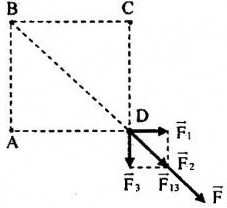
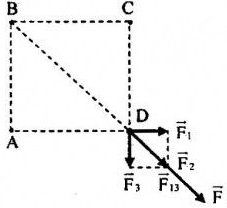
Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right| = {2.10^{ - 8}}C\\AB = BC = CD = DA = 4cm\\BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 cm\end{array} \right. \Rightarrow {F_1} = {F_3}\)
Lực tác dụng lên q4: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \)
Với: \(\left\{ \begin{array}{l}{F_1} = {F_3} = \dfrac{{k.\left| {{q_1}{q_4}} \right|}}{{A{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {{{4.10}^{ - 2}}} \right)}^2}}} = 2,{25.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_4}} \right|}}{{B{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {4\sqrt 2 {{.10}^{ - 2}}} \right)}^2}}} = 1,{125.10^{ - 3}}N\end{array} \right.\)
Ta có: \(\overrightarrow {{F_{13}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_3}} \)
Vì \(\overrightarrow {{F_1}} \bot \overrightarrow {{F_3}} \Rightarrow {F_{13}} = \sqrt {F_1^2 + F_3^2} = {F_1}\sqrt 2 = 2,25\sqrt 2 {.10^{ - 3}}N\)
Ta có: \(\overrightarrow F = \overrightarrow {{F_2}} + \overrightarrow {{F_{13}}} \)
Mà \(\overrightarrow {{F_2}} \uparrow \uparrow \overrightarrow {{F_{13}}} \Rightarrow F = {F_2} + {F_{23}} = 4,{31.10^{ - 3}}N\)
Câu hỏi 24 :
Một êlectron di chuyển trong điện trường đều E một đoạn \(0,6\,\,cm\), từ điểm M đến điểm N dọc theo một đường sức điện thì lực điện sinh công \(9,{6.10^{ - 18}}\,\,J\). Đến N êlectron di chuyển tiếp \(0,4\,\,cm\) từ điểm N đến điểm P theo phương và chiều nói trên. Tính vận tốc của êlectron khi nó đến điểm P. Biết rằng, tại M, êlectron không có vận tốc đầu. Khối lượng của êlectron là \(9,{1.10^{ - 31}}\,\,kg\).
- A \(2,{93.10^{ - 6}}\,\,m/s\)
- B \(3,{93.10^{ - 6}}\,\,m/s\)
- C \(4,{93.10^{ - 6}}\,\,m/s\)
- D \(5,{93.10^{ - 6}}\,\,m/s\)
Đáp án: D
Phương pháp giải:
Định lí động năng: Độ biến thiên động năng của một vật bằng công của ngoại lực tác dụng lên vật.
Công của lực điện: \(A = qEd\)
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{A_{MN}} = qE{d_1}}\\{{A_{NP}} = qE{d_2}}\end{array}} \right.\)
\( \Rightarrow \frac{{{A_{NP}}}}{{{A_{MN}}}} = \frac{{{d_2}}}{{{d_1}}} \Rightarrow {A_{NP}} = {A_{MN}}.\frac{{{d_2}}}{{{d_1}}} = 9,{6.10^{ - 18}}.\frac{{0,4}}{{0,6}} = 6,{4.10^{ - 18}}\,\,\left( J \right)\)
Công của lực điện khi electron di chuyển từ điểm M đến điểm P là:
\({A_{MP}} = {A_{MN}} + {A_{NP}} = (9,6 + 6,4){.10^{ - 18}} = {16.10^{ - 18}}\,\,\left( J \right)\)
Theo định lí động năng ta có:
\(\begin{array}{l}
{A_{MP}} = {{\rm{W}}_{dP}} - {{\rm{W}}_{dM}} \Rightarrow {A_{MP}} = \frac{{mv_P^2}}{2} - \frac{{mv_M^2}}{2} \Rightarrow {A_{MP}} = \frac{{mv_P^2}}{2}\\
\Rightarrow {v_P} = \sqrt {\frac{{2{A_{MP}}}}{m}} = \sqrt {\frac{{{{2.16.10}^{ - 18}}}}{{9,{{1.10}^{ - 31}}}}} = 5,{93.10^6}\,\,\left( {m/s} \right)
\end{array}\)
Câu hỏi 25 :
Một electron bay vào khoảng không giữa hai bản kim loại tích điện trái dấu với vận tốc \({v_0} = 2,{5.10^7}m/s\) từ phía bản dương về phía bản âm theo hướng hợp với bản dương góc \({15^0}\). Độ dài của mỗi bản là \(L = 5cm\) và khoảng cách giữa hai bản là \(d = 1cm\). Hãy tính hiệu điện thế giữa hai bản, biết rằng khi ra khỏi điện trường vận tốc của electron có phương song song với hai bản.
- A
\(535,5V\)
- B
\(711,7V\)
- C
\(177,7V\)
- D
\(355,5V\)
Đáp án: C
Phương pháp giải:
+ Vận dụng các biểu thức của dạng bài toán ném xiên
+ Sử dụng biểu thức tính lực điện: \(\overrightarrow F = q\overrightarrow E \)
+ Sử dụng biểu thức liên hệ giữa hiệu điện thế và cường độ điện trường: \(E = \dfrac{U}{d}\)
+ Sử dụng công thức lượng giác: \(\sin 2\alpha = 2\sin \alpha c{\rm{os}}\alpha \)
Lời giải chi tiết:
+ Chọn hệ trục \(xOy\) như hình
