Câu hỏi 1 :
Tính điện năng tiêu thụ trên dây dẫn khi dòng điện không đổi có cường độ 5A chạy qua dây dẫn trong 3 giờ, biết hiệu điện thế giữa hai dây dẫn này là 12V ?
- A 180J
- B 648000J
- C 10800J
- D 3J
Đáp án: B
Phương pháp giải:
Biểu thức tính điện năng tiêu thụ: \(A = UIt\)
Trong đó t tính bằng s.
Lời giải chi tiết:
Theo bài ra ta có: \(\left\{ \begin{array}{l}I = 5A\\U = 12V\\t = 3\,\left( h \right) = 10\,800s\end{array} \right.\)
Điện năng tiêu thụ trên dây dẫn là:
\(A = UIt = 12.5.3.60.60 = 648000J\)
Câu hỏi 2 :
Trong nguồn điện lực lạ có tác dụng
- A
làm dịch chuyển các điện tích dương từ cực dương của nguồn điện sang cực âm của nguồn điện.
- B
làm dịch chuyển các điện tích dương từ cực âm của nguồn điện sang cực dương của nguồn điện.
- C
làm dịch chuyển các điện tích dương theo chiều điện trường trong nguồn điện.
- D
làm dịch chuyển các điện tích âm ngược chiều điện trường trong nguồn điện.
Đáp án: B
Lời giải chi tiết:
Ta có: Lực lạ làm dịch chuyển điện tích dương từ cực âm sang cực dương của nguồn điện
Câu hỏi 3 :
Điện năng tiêu thụ được đo bằng.
- A
vôn kế
- B
công tơ điện
- C
ampe kế
- D
tĩnh điện kế
Đáp án: B
Lời giải chi tiết:
Điện năng tiêu thụ được đo bằng công tơ điện.
Câu hỏi 4 :
Một pin có suất điện động 1,5V và điện trở trong là \(0,5\Omega \). Mắc một bóng đèn có điện trở \(2,5\Omega \) vào hai cực của pin này thành mạch điện kín. Cường độ dòng điện chạy qua đèn là
- A 2A
- B 1A
- C 1,5A
- D 0,5A
Đáp án: D
Phương pháp giải:
Áp dụng định luật Ohm cho toàn mạch \(I = \dfrac{\xi }{{r + R}}\)
Lời giải chi tiết:
Áp dụng định luật Ohm cho toàn mạch \(I = \dfrac{\xi }{{r + R}} = \dfrac{{1,5}}{{0,5 + 2,5}} = 0,5A\)
Câu hỏi 5 :
Đặt vào hai đầu điện trở \(R\) một hiệu điện thế không đổi \(U\). Công suất toả nhiệt trên điện trở \(R\) là
- A \(P = \frac{U}{R}\).
- B \(P = UR\).
- C \(P = \frac{{{U^2}}}{R}\).
- D \(P = {U^2}R\)
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính công suất toả nhiệt: \(P = \frac{{{U^2}}}{R}\)
Lời giải chi tiết:
Công suất toả nhiệt trên \(R:\,\,P = {I^2}R = \frac{{{U^2}}}{R}.\)
Câu hỏi 6 :
Một nguồn điện được mắc với điện trở \(4,8\,\,\left( \Omega \right)\) thành mạch kín. Khi đó hiệu điện thế giữa hai cực của nguồn điện là \(12\,\,\left( V \right)\). Cường độ dòng điện trong mạch là
- A
\(I = 120\,\,\left( A \right)\)
- B
\(I = 12\,\,\left( A \right)\)
- C
\(I = 2,5\,\,\left( A \right)\)
- D
\(I = 25\,\,\left( A \right)\)
Đáp án: C
Phương pháp giải:
Hiệu điện thế giữa hai cực của nguồn điện: \(U = I.R\)
Lời giải chi tiết:
Hiệu điện thế giữa hai cực nguồn điện là:
\(U = I.R \Rightarrow I = \dfrac{U}{R} = \dfrac{{12}}{{4,8}} = 2,5\,\,\left( A \right)\)
Câu hỏi 7 :
Một nguồn điện có suất điện động là E đang cung cấp năng lượng cho mạch ngoài là một bộ bóng đèn. Biết tổng điện lượng di chuyển qua bộ bóng đèn trong thời gian t là q thì công của nguồn điện sinh ra trong thời gian t này là
- A \(A = {q^2}Et\)
- B \(A = qE\)
- C \(A = {q^2}E\)
- D \(A = qEt\)
Đáp án: B
Phương pháp giải:
+ Công thức tính công của nguồn điện: \(A = EIt\)
+ Công thức xác định cường độ dòng điện: \(I = \frac{q}{t}\)
Lời giải chi tiết:
Công của nguồn điện: \(A = EIt = E.\frac{q}{t}.t = Eq\)
Câu hỏi 8 :
Hai bóng đèn sợi đốt 12 V – 0,6 A và 12 V – 0,3 A mắc đồng thời vào mạch điện một chiều thấy chúng sáng bình thường. Trong 30 phút, điện năng hai bóng đèn tiêu thụ là
- A \(Q = 9720J\)
- B \(Q = 19440J\)
- C \(Q = 324J\)
- D \(Q = 648J\)
Đáp án: B
Phương pháp giải:
Vận dụng biểu thức tính điện năng tiêu thụ: \(Q = UIt\)
Lời giải chi tiết:
Ta có hai đèn sáng bình thường
\( \Rightarrow \) Điện năng hai bóng đèn tiêu thụ trong 30 phút:
\(Q = \left( {{U_1}{I_1} + {U_2}{I_2}} \right)t = \left( {12.0,6 + 12.0,3} \right).30.60 = 19440J\)
Câu hỏi 9 :
Hai dây dẫn đồng chất có cùng chiều dài nhưng khác tiết diện (S2 = 2S1) được mắc nối tiếp vào một mạch điện. Trong cùng một thời gian thì nhiệt lượng tỏa ra trên hai dây liên hệ với nhau qua biểu thức
- A
Q1 = 2Q2
- B
Q1 = Q2/4
- C
Q1 = 4Q2
- D
Q1 = Q2 /2
Đáp án: A
Lời giải chi tiết:
Ta có:
\(\left\{ \begin{array}{l}{R_1} = \rho \dfrac{l}{{{S_1}}}\\{R_2} = \rho \dfrac{l}{{2{S_1}}}\end{array} \right. \Rightarrow {R_1} = 2{{\rm{R}}_2}\)
Do \({R_1}nt{R_2}\) nên \(I = {I_1} = {I_2}\)
\( \Rightarrow \left\{ \begin{array}{l}{Q_1} = {I^2}{R_1}t\\{Q_2} = {I^2}\dfrac{{{R_1}}}{2}t\end{array} \right. \Rightarrow {Q_1} = 2{Q_2}\)
Câu hỏi 10 :
Cho mạch điện như hình vẽ:
Đ(24V - 0,8A), hiệu điện thế giữa hai điểm A và B được giữ không đổi U = 32V
Dịch chuyển con chạy của biến trở sao cho điện trở của biến trở R’ = 20$\Omega $. Cường độ bóng đèn như thế nào?
- A
Đèn sáng bình thường
- B
Đèn sáng yếu hơn mức bình thường
- C
Đèn sáng mạnh hơn mức bình thường
- D
Đèn cháy
Đáp án: B
Phương pháp giải:
+ Áp dụng biểu thức xác định điện trở: \(R = \frac{U}{I}\)
+ Áp dụng biểu thức xác định điện trở của toàn mạch.
Lời giải chi tiết:
Ta có:
+ Điện trở của bóng đèn:
\({R_D} = \frac{{{U_D}}}{{{I_D}}} = \frac{{24}}{{0,8}} = 30\Omega \)
+ Điện trở của biến trở: R’ = 20$\Omega $
+ Điện trở của mạch: RAB = RD + R’ = 30 + 20 = 50$\Omega $
+ Cường độ dòng điện trong mạch khi này:
\(I = \frac{U}{{{R_{AB}}}} = \frac{{32}}{{50}} = 0,64A\)
Đèn sáng bình thường khi cường độ dòng điện trong mạch là 0,8A
Ta thấy I < 0,8A => Đèn sáng yếu hơn mức bình thường
Câu hỏi 11 :
Một dây nhôm dạng hình trụ tròn được quấn thành cuộn có khối lượng 0,81kg. Tiết diện thẳng của dây là 0,1mm2. Tìm điện trở của dây đó biết rằng nhôm có khối lượng riêng và điện trở suất lần lượt là 2,7g/cm3 và 2,8.10-8$\Omega $m?
- A
84 $\Omega $
- B
480$\Omega $
- C
840$\Omega $
- D
48$\Omega $
Đáp án: C
Phương pháp giải:
+ Sử dụng công thức tính thể tích: \(V = \frac{m}{D}\)
+ Áp dụng công thức tính chiều dài dây: \(l = \frac{V}{S}\)
+ Áp dụng biểu thức xác định điện trở: \(R = \rho \frac{l}{S}\)
Lời giải chi tiết:
+ Thể tích của cuộn dây:
\(V = \frac{m}{D} = \frac{{0,81}}{{2,{{7.10}^3}}} = {3.10^{ - 4}}{m^3}\)
+ Chiều dài của dây nhôm:
\(l = \frac{V}{S} = \frac{{{{3.10}^{ - 4}}}}{{0,{{1.10}^{ - 6}}}} = 3000m\)
+ Điện trở của cuộn dây nhôm:
\(R = \rho \frac{l}{S} = 2,{8.10^{ - 8}}\frac{{3000}}{{0,{{1.10}^{ - 6}}}} = 840\Omega \)
Câu hỏi 12 :
Cho mạch điện như hình vẽ
- A
\(3A\)
- B
\(2A\)
- C
\(1A\)
- D
\(0,5A\)
Đáp án: A
Phương pháp giải:
+ Áp dụng biểu thức xác định điện trở trong mạch nối tiếp: \(R{\rm{ }} = {\rm{ }}{R_1} + {\rm{ }}{R_2} + {\rm{ }}....{\rm{ }} + {\rm{ }}{R_n}\)
+ Áp dụng biểu thức xác định điện trở trong mạch song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}\)
+ Áp dụng biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \dfrac{U}{R}\)
Lời giải chi tiết:
Từ mạch điện, ta thấy : \(\left[ {\left[ {{R_1}nt{R_2}} \right]//{R_3}} \right]nt{R_4}\)
Ta có:
+ \({R_1}nt{R_2}\) suy ra: \({R_{12}} = {R_1} + {R_2} = 1 + 2 = 3\Omega \)
+ \({R_{12}}//{R_3}\) suy ra: \(\dfrac{1}{{{R_{123}}}} = \dfrac{1}{{{R_{12}}}} + \dfrac{1}{{{R_3}}} \Rightarrow {R_{123}} = \dfrac{{{R_{12}}.{R_3}}}{{{R_{12}} + {R_3}}} = \dfrac{{3.2}}{{3 + 2}} = 1,2\Omega \)
+ \({R_{123}}nt{R_4}\) suy r: \({R_{td}} = {R_{123}} + {R_4} = 1,2 + 0,8 = 2\Omega \)
Cường độ dòng điện trong mạch: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{6}{2} = 3A\)
Câu hỏi 13 :
Cho mạch điện có sơ đồ như hình vẽ:
Biết: E = 1,5 V, r = 1\(\Omega \), R = 6\(\Omega \). Cường độ dòng điện qua mạch chính là?
- A
1,5V
- B
0,75A
- C
4V
- D
4,8V
Đáp án: B
Phương pháp giải:
+ Áp dụng biểu thức xác định suất điện động bộ nguồn khi mắc hỗn hợp đối xứng: Eb = m.E.
+ Áp dụng biểu thức xác định suất điện động bộ nguồn mắc nối tiếp
+ Áp dụng biểu thức xác định điện trở trong của bộ nguồn khi mắc hỗn hợp đối xứng: \(\;{r_b} = \frac{{m.r}}{n}\)
+ Áp dụng biểu thức xác định điện trở trong của bộ nguồn mắc nối tiếp
+ Áp dụng định luật Ôm cho toàn mạch
Lời giải chi tiết:
Ta có:
- Suất điện động bộ nguồn : Eb = 2E + 3E = 5E = 5.1,5 = 7,5V
- Điện trở trong bộ nguồn :
\(\;{r_b} = \dfrac{{2.r}}{2} + 3{\rm{r}} = 4{\rm{r}} = 4.1 = 4\Omega \).
Cường độ dòng điện trong mạch chính :
\(I = \dfrac{{{E_b}}}{{R + {r_b}}} = \dfrac{{7,5}}{{6 + 4}} = 0,75A\)
Câu hỏi 14 :
Cho mạch điện như hình vẽ:
e1 = 6V, e2 = 18V, r1 = r2 = 2$\Omega $; R0 = 4$\Omega $. Đèn ghi 6V - 6W. R là biến trở.
R = ? để đèn sáng bình thường
- A
4$\Omega $
- B
9$\Omega $
- C
4,5 $\Omega $
- D
2$\Omega $
Đáp án: C
Phương pháp giải:
+ Áp dụng định luật Ôm cho đoạn mạch
+ Áp dụng biểu thức: P = UI = U2/R
Lời giải chi tiết:
Khi R = 6$\Omega $. Ta xét nguồn điện tương đương gồm hai nhánh chứa hai nguồn e1 và e2.
Giả sử cực dương của nguồn tương đương ở A. Biến trở R và đèn là mạch ngoài.
\(\frac{1}{{{r_b}}} = \frac{1}{{{r_1} + {R_0}}} + \frac{1}{{{r_2}}} \to {r_b} = 1,5\Omega \)
\({e_b} = \frac{{\frac{{{e_1}}}{{{r_1} + {R_0}}} - \frac{{{e_2}}}{{{r_2}}}}}{{\frac{1}{{{r_b}}}}} = - 12V < 0\)
=> Cực dương của nguồn tương đương ở B.
Ta có điện trở của đèn:
\({R_D} = \frac{{{U^2}}}{P} = \frac{{{6^2}}}{6} = 6\Omega \)
Cường độ dòng điện định mức của đèn:
\({I_{dm}} = \frac{P}{U} = \frac{6}{6} = 1A\)
\({I_d} = I = \frac{{{e_b}}}{{R + {R_d} + {r_b}}}\)
Để đèn sáng bình thường thì I = Iđm
\({I_d} = I = \frac{{{e_b}}}{{R + {R_d} + {r_b}}} = {I_{dm}} = 1A \leftrightarrow \frac{{12}}{{R + 6 + 1,5}} = 1 \to R = 4,5\Omega \)
Câu hỏi 15 :
Cho mạch điện như hình vẽ: E1 = 12V, E2 = 9V, E3 = 3V, r1 = r2 = r3 = 1$\Omega $. Các điện trở R1 = R2 = R3 = 2$\Omega $. Hiệu điện thế UAB có giá trị:
- A
2V
- B
4V
- C
9V
- D
6V
Đáp án: A
Câu hỏi 16 :
Cho mạch điện sau:
Biết E = 24V, r = 2$\Omega $, R1 = R2 = 5$\Omega $, C1 = 4.10-7F, C2 = 6.10-7F.
Điện tích trên 2 bản tụ điện khi K mở là
- A
Q1 = Q2 = 4,8.10-6C
- B
Q1 = 2,4.10-7C, Q2 = 4,8.10-6C
- C
Q1 = Q2 = 2,4.10-7C
- D
Q1 = 4,8.10-6C , Q2 = 2,4.10-7C
Đáp án: A
Phương pháp giải:
+ Áp dụng định luật Ôm cho toàn mạch: \(I = \frac{E}{{{R_N} + r}}\)
+ Áp dụng biểu thức tính điện dung nối tiếp: \(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}}\)
+ Áp dụng biểu thức Q = CU
Lời giải chi tiết:
Ta có: Dòng điện một chiều không qua tụ điện nên khi khóa K mở - dòng điện chỉ chạy qua R1 và R2.
Dòng điện chạy trong mạch:
\(I = \frac{E}{{{R_1} + {R_2} + r}} = \frac{{24}}{{5 + 5 + 2}} = 2(A)\)
+ Khi đó, R1 và R2 mắc nối tiếp nhau nên hiệu điện thế giữa hai điểm A và B là: UAB = I.R12 = 2.10 = 20V
+ Vì hai tụ điện mắc nối tiếp nên điện dung của bộ tụ là:
\(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} \to C = \frac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = 2,{4.10^{ - 7}}F\)
+ Hiệu điện thế của bộ tụ C là: U = UAB = 20V
Vì hai tụ điện mắc nối tiếp nên: Q1 = Q2 = Q = CU = 2,4.10-7.20 = 4,8.10-6C
Câu hỏi 17 :
Mạch điện mắc như hình vẽ, nguồn điện có suất điện động ξ, điện trở trong r. Biết ampe kế và vôn kế đều lí tưởng. Ampe kế chỉ 3 A, vôn kế chỉ 18 V. Biết hiệu suất của nguồn điện là 60 %. Suất điện động và điện trở trong của nguồn nhận giá trị là:
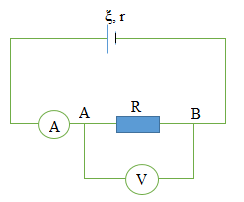
- A 30V; 4Ω
- B 30V; 2Ω
- C 10,8V; 4Ω
- D 10,8V; 2Ω
Đáp án: A
Phương pháp giải:
Áp dụng công thức định luật Ôm cho đoạn mạch để tìm điện trở R:
\(I = \frac{U}{R} \Rightarrow R = \frac{U}{I}\)
Áp dụng công thức về hiệu suất của nguồn:
\(H = \frac{R}{{R + r}}.100\% \)
Áp dụng công thức định luật Ôm cho toàn mạch:
\(I = \frac{\xi }{{R + r}} \Rightarrow \xi = I.(R + r)\)
Lời giải chi tiết:
Áp dụng công thức định luật Ôm cho đoạn mạch ta có:
\(I = \frac{U}{R} \Rightarrow R = \frac{U}{I} = \frac{{18}}{3} = {6_{}}\Omega \)
Áp dụng công thức về hiệu suất của nguồn :
\(H = \frac{R}{{R + r}}.100\% \Rightarrow \frac{R}{{R + r}} = 0,6 \Rightarrow \frac{6}{{6 + r}} = 0,6 \Rightarrow r = {4_{}}\Omega \)
Áp dụng công thức định luật Ôm cho toàn mạch:
\(I = \frac{\xi }{{R + r}} \Rightarrow \xi = I.(R + r) = 3.(6 + 4) = 30\left( V \right)\)
Câu hỏi 18 :
Để xác định điện trở trong r của một nguồn điện, một học sinh mắc mạch điện như hình (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của số chỉ U của vôn kế V vào số chỉ I của ampe kế A như hình (H2). Điện trở của vôn kế rất lớn. Biết \({R_0} = 2{\rm{0,3 \Omega }}\). Giá trị của r được xác định bởi thí nghiệm này là
- A
\({\rm{0,49 \Omega }}\)
- B
\({\rm{0,85 \Omega }}\)
- C
\({\rm{1,0 \Omega }}\)
- D
\({\rm{1,5 \Omega }}\)
Đáp án: A
Phương pháp giải:
Áp dụng công thức: \(U = \xi - I({R_0} + r)\)
Câu hỏi 19 :
Cho mạch điện như hình vẽ:
- A
\(7V\)
- B
\(2V\)
- C
\(5V\)
- D
\(4V\)
Đáp án: A
Phương pháp giải:
+ Sử dụng biểu thức tính điện trở tương đương của các điện trở mắc nối tiếp: \(R = {R_1} + {R_2} + ...\)
+ Sử dụng biểu thức tính điện trở tương đương của các điện trở mắc song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ...\)
+ Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\)
+ Sử dụng biểu thức định luật ôm.
Lời giải chi tiết:
+ Từ mạch điện ta thấy: \(\left( {\left[ {{R_2}nt{R_3}} \right]//{R_1}} \right)nt{R_4}\)
\({R_{23}} = {R_2} + {R_3} = 3 + 3 = 6\Omega \)
\({R_{AB}} = \dfrac{{{R_1}{R_{23}}}}{{{R_1} + {R_{23}}}} = \dfrac{{3.6}}{{3 + 6}} = 2\Omega \)
Tổng trở của mạch ngoài: \({R_N} = {R_{AB}} + {R_4} = 2 + 6 = 8\Omega \)
+ Cường độ dòng điện trong mạch chính: \(I = \dfrac{E}{{{R_N} + r}} = \dfrac{9}{{8 + 1}} = 1A\)
\({I_4} = {I_{AB}} = I = 1A\)
+ Hiệu điện thế giữa hai điểm A, B: \({U_{AB}} = {I_{AB}}.{R_{AB}} = 1.2 = 2V\)
Suy ra: \({U_1} = {U_{23}} = 2V\)
+ Dòng điện chạy qua \({R_1}\): \({I_1} = \dfrac{{{U_1}}}{{{R_1}}} = \dfrac{2}{3}\left( A \right)\)
+ Dòng điện qua \({R_2}\) và \({R_3}\) là: \({I_{23}} = {I_2} = {I_3} = I - {I_1} = 1 - \dfrac{2}{3} = \dfrac{1}{3}A\)
+ Hiệu điện thế giữa hai đầu mỗi điện trở \({R_2}\) và \({R_3}\) là: \(\left\{ \begin{array}{l}{U_2} = {I_2}.{R_2} = \dfrac{1}{3}.3 = 1V\\{U_3} = {I_3}.{R_3} = \dfrac{1}{3}.3 = 1V\end{array} \right.\)
+ Hiệu điện thế qua \(R_4\) là \(U_4=I_4.R_4=1.6=6V\)
Hiệu điện thế giữa hai điểm C và D : \({U_{CD}} = {U_3} + {U_4} = 1 + 6 = 7V\)
Câu hỏi 20 :
Cho mạch điện như hình vẽ:
- A
\(2V\)
- B
\(8V\)
- C
\(6V\)
- D
\(4V\)
Đáp án: A
Phương pháp giải:
Áp dụng định luật Ôm cho đoạn mạch
Lời giải chi tiết:
- Giả sử \({R_V}\) vô cùng lớn: \({R_V}\; = \infty \)
Số chỉ trên \({V_1}\) là: \({U_1} = 5R\dfrac{E}{{6R}} = \dfrac{5}{6}E = \dfrac{5}{6}.12 = 10V\)
Điều này trái với giả thiết => điều giả sử là sai hay \({R_V}\) hữu hạn.
- Ta có: \({U_{AC}} = 12V \Rightarrow {U_{BC}} = 6V\)
\( \Rightarrow {R_{CMNB}} = R \Leftrightarrow \dfrac{{(2R + {R_{PQ}}){R_V}}}{{2R + {R_{PQ}} + {R_V}}} = R\)
Với \({R_{PQ}} = \dfrac{{3R.{R_V}}}{{3R + {R_V}}} \to {R_V} = 1,5R\)
Số chỉ trên \({V_2}\): \({U_2} = \dfrac{{{U_{BC}}}}{{3R}}R = \dfrac{6}{3} = 2V\)
