Đề bài
Cho đường tròn (O) dây cung AB. Tiếp tuyến của (O) tại A và B cắt nhau tại M. Biết \(\widehat {AMB} = 50^\circ \).
a) Tính số đo cung AB.
b) Trên nửa mặt phẳng bờ OB ( không chứa điểm A), kẻ đườngthẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.
Phương pháp giải - Xem chi tiết
a. Chứng minh tứ giác AOBM có tổng hai góc đối bằng 180 độ
b.Tính số đo cung ADB từ đó ta tính được số đo cung AD
Lời giải chi tiết
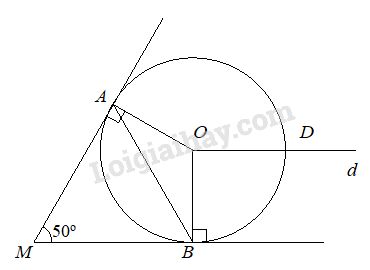
a) MA, MB là hai tiếp tuyến của (O) nên MA \( \bot \) OA và MB \( \bot \) OB.
Xét tứgiác AOBM có:
\(\widehat {AOB} = 360^\circ - (\widehat {MAO} + \widehat {MBO} + \widehat {AMB}) \)\(\;= 360^\circ - (90^\circ + 90^\circ + 50^\circ ) = 130^\circ \).
\(sd \overparen {AB}=sd\overparen{AOB}=130^o\)
b) Ta có: \(sd\overparen {ADB} = 360^o − \overparen {AB} = 360^o − 130^o\)\(\;= 230^o\)
Mặt khác OD // BM mà BM \( \bot \) OB \(\Rightarrow\) OD \( \bot \) OB
hay \(sd\overparen{AD} = sd\overparen{ADB }– sd\overparen{BD} \)\(\,= 230^o− 90^o=140^o\)
soanvan.me
