Đề bài
Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm phân biệt A và B. Biết rằng hai cung nhỏ AB của hai đường tròn này có số đo (độ) bằng nhau. Chứng minh rằng hai đường tròn (O) và (O') bằng nhau.
Phương pháp giải - Xem chi tiết
+Hai cung nhỏ AB của hai đường tròn này có số đo (độ) bằng nhau nên \( \Rightarrow \widehat {AOB} = \widehat {AO'B}\)
+Hai tam giác ABO và tam giác ABO' cân tại O nên suy ra bốn góc ở đáy của hai tam giác này bằng nhau. Từ đó ta chứng minh được hai tam giác này bằng nhau
Lời giải chi tiết
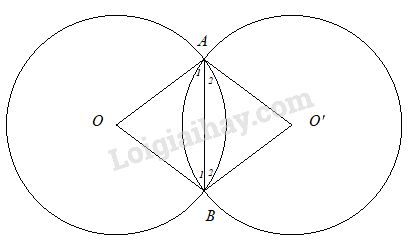
Ta có: Hai cung nhỏ AB của hai đường tròn này có số đo (độ) bằng nhau \( \Rightarrow \widehat {AOB} = \widehat {AO'B}\)
Mặt khác các tam giác AOB và AO'B có hai góc ở đỉnh bằng nhau nên bốn góc ở đáy cũng bằng nhau : \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}}\)
Do đó \(∆AOB = ∆AO'B\) (c.g.c) \(\Rightarrow OA = O'A\)
Chứng tỏ hai đường tròn (O) và (O’) bằng nhau.
soanvan.me
