Lý thuyết góc ở tâm. số đo cung

1. Lý thuyết góc ở tâm

- Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

Ví dụ: \(\widehat {AOB}\) là góc ở tâm (hình $1$ ).

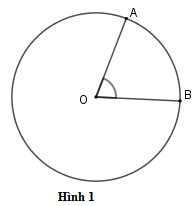
- Nếu \({0^0} < \alpha  < {180^0}\) thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn.

- Nếu \(\alpha  = {180^0}\) thì mỗi cung là một nửa đường tròn.

- Cung nằm bên trong góc được gọi là cung bị chắn. Góc bẹt chắn nửa đường tròn.

- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Ví dụ: \(\widehat {AOB} = \) số đo cung $AB$ (góc ở tâm chắn cung \(AB\)) (hình 1)

- Số đo của cung lớn bằng hiệu giữa \({360^0}\) và số đo của cung nhỏ (có chung $2$  mút với cung lớn).

- Số đo của nửa đường tròn bằng \({180^0}\) . Cả đường tròn có số đo \({360^0}.\) Cung không có số đo \({0^0}\) (cung có $2$  mút trùng nhau).

Trong một đường tròn hay hai đường tròn bằng nhau:

- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

- Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Nếu $C$ là một điểm nằm trên cung $AB$  thì

sđ $\overparen{AB}= $ sđ $\overparen{AC} +$ sđ $\overparen{CB}$.

2. Các dạng toán thường gặp

Dạng 1: Tính số đo của góc ở tâm, tính số đo của cung bị chắn. So sánh các cung.

Phương pháp:

Ta sử dụng các kiến thức sau:

- Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó

- Số đo của cung lớn bằng hiệu giữa \({360^0}\) và số đo của cung nhỏ (có chung hai đầu mút với cung lớn).

- Số đo của nửa đường tròn bằng \({180^0}.\) Cung cả đường tròn có số đo \({360^0}.\)

- Sử dụng tỉ số lượng giác của một góc nhọn để tính góc.

- Sử dụng quan hệ đường kính và dây cung.