Câu hỏi 1 :
Khi nói về sóng điện từ. Phát biểu nào sau đây sai?
- A Tại một điểm có sóng điện từ truyền qua, điện trường và từ trường biến thiên cùng tần số nhưng ngược pha.
- B Tốc độ lan truyền sóng điện từ trong các điện môi thì nhỏ hơn trong chân không.
- C Nếu tại một nơi có điện trường biến thiên theo thời gian thì tại nơi đó xuất hiện từ trường.
- D Khi sóng điện từ gặp mặt phân cách giữa hai môi trường thì nó bị phản xạ và khúc xạ.
Đáp án: A
Phương pháp giải:
Sử dụng lí thuyết về sóng điện từ.
Lời giải chi tiết:
Tại một điểm có sóng điện từ truyền qua, điện trường và từ trường biến thiên cùng tần số, cùng pha.
\( \Rightarrow \) Phát biểu sai là: Tại một điểm có sóng điện từ truyền qua, điện trường và từ trường biến thiên cùng tần số nhưng ngược pha.
Câu hỏi 2 :
Một chất điểm dao động điều hòa có phương trình \(x = 4\cos \left( {20\pi t + \frac{\pi }{3}} \right)cm\). Tần số dao động của chất điểm là
- A 20 Hz.
- B 10 Hz.
- C \(10\pi {\rm{ }}Hz\) .
- D \(20\pi {\rm{ }}Hz\)
Đáp án: B
Phương pháp giải:
Tần số dao động: \(f = \frac{\omega }{{2\pi }}\)
Lời giải chi tiết:
Từ phương trình \(x = 4\cos \left( {20\pi t + \frac{\pi }{3}} \right)cm\)\( \Rightarrow \omega = 20\pi \,rad/s\)
\( \Rightarrow \) Tần số dao động: \(f = \frac{\omega }{{2\pi }} = \frac{{20\pi }}{{2\pi }} = 10Hz\)
Câu hỏi 3 :
Sóng vô tuyến được ứng dụng trong thông tin liên lạc giữa Trái Đất và vệ tinh là
- A sóng trung.
- B sóng dài.
- C sóng cực ngắn.
- D sóng ngắn
Đáp án: C
Phương pháp giải:
Sử dụng bảng đặc điểm và ứng dụng của các loại sóng vô tuyến.
Lời giải chi tiết:
Ta có bảng:

\( \Rightarrow \) Sóng vô tuyến được ứng dụng trong thông tin liên lạc giữa Trái Đất và vệ tinh là sóng cực ngắn.
Câu hỏi 4 :
Hai điện tích điểm đặt cách nhau một khoảng r, trong chân không. Lực tương tác điện giữa chúng có độ lớn tỉ lệ với
- A \(\frac{1}{r}\)
- B \(\frac{1}{{{r^2}}}\)
- C \({r^2}\)
- D \(r\)
Đáp án: B
Phương pháp giải:
Công thức tính lực tương tác giữa hai điện ticshddiemer: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Lời giải chi tiết:
Độ lớn lực tương tác giữa hai điện tích điểm: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \Rightarrow F \sim \frac{1}{{{r^2}}}\)
Câu hỏi 5 :
Một trong những ứng dụng của tia tử ngoại là
- A diệt khuẩn.
- B chiếu điện, chụp điện.
- C sấy nông sản.
- D chụp ảnh trong bóng tối
Đáp án: A
Phương pháp giải:
Ứng dụng của tia tử ngoại
- Trong y học, tia tử ngoại được sử dụng để tiệt trùng các dụng cụ phẫu thuật, để chữa một số bệnh.
- Trong công nghiệp thực phẩm, tia tử ngoại được sử dụng để tiệt trùng cho thực phẩm trước khi đóng gói hoặc đóng hộp.
Lời giải chi tiết:
Một trong những ứng dụng của tia tử ngoại là diệt khuẩn.
Câu hỏi 6 :
Sóng cơ không lan truyền được trong môi trường nào sau đây?
- A Chất lỏng.
- B Chất khí.
- C Chất rắn.
- D Chân không.
Đáp án: D
Phương pháp giải:
Sóng cơ lan truyền được trong các môi trường rắn, lỏng, khí.
Sóng cơ không lan truyền được trong chân không.
Lời giải chi tiết:
Sóng cơ không lan truyền được trong môi trường chân không.
Câu hỏi 7 :
Tiếng trống trường khi lan truyền trong không khí là
- A sóng ngang.
- B siêu âm.
- C sóng dọc.
- D hạ âm.
Đáp án: C
Phương pháp giải:
+ Sóng âm là những sóng cơ truyền trong các môi trường rắn, lỏng, khí.
+ Trong chất khí và chất lỏng, sóng âm là sóng dọc vì trong các chất này lực đàn hồi chỉ xuất hiện khi có biến dạng nén, dãn.
Lời giải chi tiết:
Tiếng trống trường khi lan truyền trong không khí là sóng dọc.
Câu hỏi 8 :
Một con lắc đơn có chiều dài \(\ell \) dao động điều hòa trong trọng trường có gia tốc trọng trường g. Tần số dao động của con lắc được tính bằng
- A \(2\pi \sqrt {\frac{g}{l}} \)
- B \(\frac{1}{{2\pi }}\sqrt {\frac{l}{g}} \)
- C \(2\pi \sqrt {\frac{l}{g}} \)
- D \(\frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
Đáp án: D
Phương pháp giải:
Tần số góc, chu kì, tần số dao động của con lắc đơn:
\(\omega = \sqrt {\frac{g}{l}} ;T = 2\pi \sqrt {\frac{l}{g}} ;f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
Lời giải chi tiết:
Tần số dao động của con lắc đơn:\(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
Câu hỏi 9 :
Hiện tượng quang điện ngoài là hiện tượng các eletron bị bật ra khỏi bản kim loại do
- A khối kim loại có nhiệt độ cao.
- B tác dụng của ánh sáng có bước sóng thích hợp
- C tác dụng của từ trường mạnh.
- D tác dụng của ánh sáng có cường độ lớn.
Đáp án: B
Phương pháp giải:
Hiện tượng ánh sáng làm bật các electron ra khỏi bề mặt kim loại gọi là hiện tượng quang điện ngoài.
Lời giải chi tiết:
Hiện tượng quang điện ngoài là hiện tượng các eletron bị bật ra khỏi bản kim loại do tác dụng của ánh sáng có bước sóng thích hợp.
Câu hỏi 10 :
Khi chiếu một chùm tia tử ngoại vào một ống nghiệm đựng dung dịch fluorexein thì thấy dung dịch này phát ra ánh sáng màu lục. Đây là hiện tượng
- A hóa – phát quang.
- B phản xạ ánh sáng.
- C tán sắc ánh sáng.
- D quang – phát quang
Đáp án: D
Phương pháp giải:
Hiện tượng quang – phát quang là hiện tượng một số chất có khả năng hấp thụ ánh sáng có bước sóng này để phát ra một ánh sáng có bước sóng khác. Ví dụ: Nếu chiếu một chùm bức xạ tử ngoại vào một ống nghiệm chứa dung dịch fluorexêin. Sau đó ta sẽ thấy dung dịch phát ra ánh sáng màu lục.
Lời giải chi tiết:
Khi chiếu một chùm tia tử ngoại vào một ống nghiệm đựng dung dịch fluorexein thì thấy dung dịch này phát ra ánh sáng màu lục. Đây là hiện tượng quang – phát quang.
Câu hỏi 11 :
Hai nguyên tử A và B là đồng vị của nhau, hạt nhân của chúng có cùng
- A số nuclôn.
- B số nơtrôn.
- C khối lượng.
- D số prôtôn
Đáp án: D
Phương pháp giải:
Đồng vị là những nguyên tử mà hạt nhân chứa cùng số proton Z nhưng có số notron N khác nhau.
Lời giải chi tiết:
Hai nguyên tử A và B là đồng vị của nhau, hạt nhân của chúng có cùng số proton.
Câu hỏi 12 :
Khi nói về tia X, phát biểu nào sau đây không đúng ?
- A Tia X làm ion hóa không khí.
- B Tia X gây ra phản ứng quang hợp.
- C Tia X còn có tên gọi khác là tia Rơn – ghen.
- D Tia X không bị lệch khi truyền trong điện trường
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về tia X.
Lời giải chi tiết:
+ Tia X làm ion hóa không khí \( \Rightarrow \) Đúng vì nó năng lượng lớn.
+ Tia X gây ra phản ứng quang hợp \( \Rightarrow \) Sai vì tia tử ngoại mới gây ra phản ứng quang hợp.
+ Tia X còn có tên gọi khác là tia Rơn – ghen \( \Rightarrow \) Đúng.
+ Tia X không bị lệch khi truyền trong điện trường \( \Rightarrow \) Đúng vì tia X không mang điện tích.
Câu hỏi 13 :
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm \({10^{ - 4}}H\) và tụ điện có điện dung C. Biết tần số dao động riêng của mạch là 100 kHz. Lấy \({\pi ^2} = 10\). Giá trị của C là
- A 25 nF.
- B 0,25 F.
- C 250 nF.
- D 0,025 F.
Đáp án: A
Phương pháp giải:
Tần số của mạch dao động: \(f = \frac{1}{{2\pi \sqrt {LC} }}\)
Lời giải chi tiết:
Từ công thức tính tần số dao động của mạch dao động ta có:
\(\begin{array}{l}f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow C = \frac{1}{{4{\pi ^2}{f^2}L}}\\ \Rightarrow C = \frac{1}{{4.10.{{\left( {{{100.10}^3}} \right)}^2}{{.10}^{ - 4}}}} = 2,{5.10^{ - 8}}F = 25nF\end{array}\)
Câu hỏi 14 :
Nếu một con lắc đang dao động duy trì thì
- A cả biên độ dao động và tần số của dao động đều không đổi.
- B biên độ dao động không đổi, tần số của dao động giảm dần.
- C cả biên độ dao động và tần số của dao động đều giảm dần.
- D biên độ dao động giảm dần, tần số của dao động không đổi.
Đáp án: A
Phương pháp giải:
Sử dụng lí thuyết về dao động duy trì.
Lời giải chi tiết:
Nếu một con lắc đang dao động duy trì thì cả biên độ dao động và tần số của dao động đều không đổi.
Câu hỏi 15 :
Năng lượng cần thiết để giải phóng một eletron liên kết thành một eletron dẫn (năng lượng kích hoạt) của Ge là 0,66eV. Lấy \(h = 6,{625.10^{ - 3}}4{\rm{ }}\left( {J.s} \right);{\rm{ }}c = {3.10^8}{\rm{ }}\left( {m/s} \right)\) và \(1eV = 1,{6.10^{ - 19}}\left( J \right)\). Giới hạn quang dẫn của Ge là
- A 1,88 nm.
- B 8,18 nm.
- C \(1,88\mu m\)
- D \(8,18\mu m\)
Đáp án: C
Phương pháp giải:
Giới hạn quang dẫn: \({\lambda _0} = \frac{{hc}}{A}\)
Lời giải chi tiết:
Giới hạn quang dẫn của Ge là:
\({\lambda _0} = \frac{{hc}}{A} = \frac{{6,{{625.10}^{ - 3}}{{.3.10}^8}}}{{0,66.1,{{6.10}^{ - 19}}}} = 1,{88.10^{ - 6}}m = 1,88\mu m\)
Câu hỏi 16 :
Dòng điện xoay chiều có cường độ hiệu dụng bằng \(2\sqrt 2 A\) thì giá trị cường độ dòng điện cực đại là
- A 2A
- B 0,5A
- C 0,25A
- D 4A
Đáp án: D
Phương pháp giải:
Công thức liên hệ giữa cường độ dòng điện cực đại và hiệu dụng: \(I = \frac{{{I_0}}}{{\sqrt 2 }}\)
Lời giải chi tiết:
Cường độ dòng điện cực đại là: \({I_0} = I.\sqrt 2 = 2\sqrt 2 .\sqrt 2 = 4A\)
Câu hỏi 17 :
Từ không khí, chiếu xiên một chùm sáng hẹp song song (coi là một tia sáng) gồm các bức xạ đơn sắc tím, đỏ, lam, vàng vào trong nước. So với phương của tia tới, độ lệch tia khúc xạ theo thứ tự tăng dần là
- A đỏ, vàng, lam, tím
- B tím, lam, vàng, đỏ
- C tím, vàng, lam, đỏ
- D đỏ, lam, vàng, tím
Đáp án: A
Phương pháp giải:
Biểu thức của định luật khúc xạ ánh sáng: \({n_1}.\sin i = {n_2}\sin \,r\)
Với chiết suất của môi trường đối với ánh sáng đơn sắc: \({n_d} < {n_t}\)
Lời giải chi tiết:
Khi ánh sáng truyền từ không khí vào nước: \(\sin i = n.\sin \,r \Rightarrow \sin \,r = \frac{{\sin i}}{n}\)
Mà \({n_d} < {n_t} \Rightarrow {r_d} > {r_t}\)
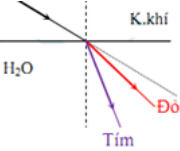
\( \Rightarrow \) So với phương của tia tới, độ lệch tia khúc xạ theo thứ tự tăng dần là: đỏ, vàng, lam, tím.
Câu hỏi 18 :
Quang phổ của một vật rắn nóng sáng phát ra là
- A một dải có 7 màu.
- B một hệ thống gồm các vạch tối trên dải màu sắc biến đổi liên tục.
- C một dải các màu sắc biến đổi liên tục.
- D một hệ thống gồm cách vạch màu ngăn cách bởi các khoảng tối.
Đáp án: C
Phương pháp giải:
Sử dụng lí thuyết về nguồn phát của: quang phổ liên tục, quang phổ vạch phát xạ, quang phổ vạch hấp thụ.
Lời giải chi tiết:
Quang phổ của một vật rắn nóng sáng phát ra là một dải các màu sắc biến đổi liên tục.
Câu hỏi 19 :
Mắc một điện trở \(10\Omega \) vào hai cực của một bộ pin có suất điện động E = 6V, điện trở trong \(r = 2\Omega \). Cường độ dòng điện trong mạch bằng
- A 0,6A
- B 1,2A
- C 0,5A
- D 3,0A
Đáp án: C
Phương pháp giải:
Biểu thức định luật Ôm: \(I = \frac{\xi }{{{R_N} + r}}\)
Lời giải chi tiết:
Cường độ dòng điện trong mạch bằng: \(I = \frac{\xi }{{{R_N} + r}} = \frac{6}{{10 + 2}} = 0,5A\)
Câu hỏi 20 :
Đặt điện áp \(u = {U_0}\cos \left( {100\pi t + \frac{\pi }{2}} \right)V\) vào hai đầu một mạch điện ghép nối tiếp gồm điện trở thuần, cuộn cảm thuần và tụ điện đều có giá trị khác 0. Pha ban đầu của dòng điện qua mạch \(({\varphi _i})\) có giá trị
- A \(0 \le {\varphi _i} \le \pi \)
- B
\( - \dfrac{\pi }{2} \le {\varphi _i} \le \dfrac{\pi }{2}\)
- C
\( - \dfrac{\pi }{2} < {\varphi _i} < \dfrac{\pi }{2}\)
- D \(0 < {\varphi _i} < \pi \)
Đáp án: D
Phương pháp giải:
Sử dụng giản đồ vecto.
Độ lệch pha giữa u và i: \(\varphi = {\varphi _u} - {\varphi _i}\)
Lời giải chi tiết:
Độ lệch pha giữa u và i: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Ta có giản đồ vecto:
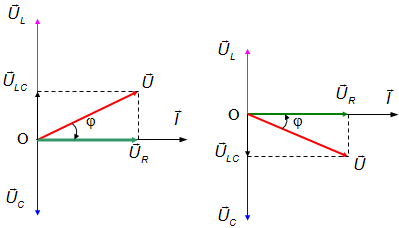
Từ giản đồ vecto ta thấy: \( - \frac{\pi }{2} < \varphi < \frac{\pi }{2}\)
\( - \frac{\pi }{2} < {\varphi _u} - {\varphi _i} < \frac{\pi }{2} \Leftrightarrow - \frac{\pi }{2} < \frac{\pi }{2} - {\varphi _i} < \frac{\pi }{2} \Leftrightarrow 0 < {\varphi _i} < \pi \)
Câu hỏi 21 :
Điện áp xoay chiều ở hai đầu một thiết bị điện lệch pha \(\frac{\pi }{6}\) so với cường độ dòng điện chạy qua thiết bị đó. Hệ số công suất của thiết bị lúc này bằng
- A 1,00
- B 0,87
- C 0,50
- D 0,70
Đáp án: B
Phương pháp giải:
Hệ số công suất: \(\cos \varphi ;\,\varphi = {\varphi _u} - {\varphi _i}\)
Lời giải chi tiết:
Hệ số công suất của thiết bị này bằng: \(\cos \varphi = \cos \frac{\pi }{6} = 0,87\)
Câu hỏi 22 :
Âm sắc là một đặc trưng sinh lí của âm cho phép ta phân biệt được các âm
- A có cùng độ to do các nhạc cụ khác nhau phát ra
- B có cùng biên độ do các nhạc cụ khác nhau phát ra
- C có cùng tần số do các nhạc cụ khác nhau phát ra
- D có cùng biên độ do một nhạc cụ phát ra ở các thời điểm khác nhau
Đáp án: C
Phương pháp giải:
Sử dụng lí thuyết về các đặc trưng sinh lí của âm.
Lời giải chi tiết:
Âm sắc là một đặc trưng sinh lí của âm cho phép ta phân biệt được các âm có cùng tần số do các nhạc cụ khác nhau phát ra.
Câu hỏi 23 :
Roto của máy phát điện xoay chiều với nam châm có 3 cặp cực từ, quay với tốc độ 1200 vòng/phút. Tần số của suất điện động do máy tạo ra là
- A 70 Hz
- B 60 Hz
- C 50 Hz
- D 40 Hz
Đáp án: B
Phương pháp giải:
Công thức tính tần số: \(f = \frac{{np}}{{60}}\,\,\,\left( {Hz} \right)\)
Trong đó: p là số cặp cực; n là tốc độ quay của roto tính bằng vòng/phút.
Lời giải chi tiết:
Tần số của suất điện động do máy tạo ra là:
\(f = \frac{{np}}{{60}} = \frac{{3.1200}}{{60}}\, = 60\,\,\left( {Hz} \right)\)
Câu hỏi 24 :
Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số và có cùng biên độ là 4 cm. Nếu biên độ dao động tổng hợp cũng là 4 cm thì độ lớn độ lệch pha của dao động tổng hợp với dao động thành phần là
- A \(\frac{\pi }{3}\)
- B \(\frac{{2\pi }}{3}\)
- C \(\frac{\pi }{6}\)
- D \(\frac{\pi }{2}\)
Đáp án: A
Phương pháp giải:
Ta có: \(\left\{ \begin{array}{l}{x_1} = {A_1}.cos\left( {\omega t + {\varphi _1}} \right)\\{x_2} = {A_2}.cos\left( {\omega t + {\varphi _2}} \right)\\x = {x_1} + {x_2} = A.cos\left( {\omega t + \varphi } \right)\end{array} \right.\)
Với \(A_2^2 = {A^2} + A_1^2 - 2A.{A_1}.\cos \left( {\varphi - {\varphi _1}} \right)\)
Lời giải chi tiết:
Ta có: \({A_2} = {A^2} + A_1^2 - 2A.{A_1}.\cos \left( {\varphi - {\varphi _1}} \right)\)
\(\begin{array}{l} \Leftrightarrow {4^2} = {4^2} + {4^2} - 2.4.4.cos\left( {\varphi - {\varphi _1}} \right)\\ \Leftrightarrow cos\left( {\varphi - {\varphi _1}} \right) = \frac{1}{2} \Rightarrow \left( {\varphi - {\varphi _1}} \right) = \frac{\pi }{3}\end{array}\)
Câu hỏi 25 :
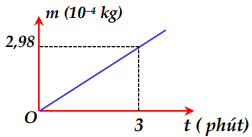
Một bình điện phân chứa dung dịch đồng sunphat \(\left( {CuS{O_4}} \right)\) với hai điện cực bằng đồng (Cu) . Người ta cho dòng điện không đổi có cường độ 5A chạy qua bình điện phân này rồi ghi lại độ tăng khối lượng của catốt theo thời gian. Đồ thị biểu diễn sự phụ thuộc của khối lượng catốt tăng lên theo thời gian được biểu diễn như hình bên. Đương lượng điện hóa của đồng (Cu) xác định được từ số liệu ở đồ thị trên là
- A \(3,{31.10^{ - 7}}\left( {Kg/C} \right)\)
- B \(3,{31.10^{ - 7}}\left( {g/C} \right)\)
- C \(3,{31.10^{ - 3}}\left( {g/C} \right)\)
- D \(.3,{31.10^{ - 3}}\left( {Kg/C} \right)\)
Đáp án: A
Phương pháp giải:
+ Định luật Faraday thứ nhất: Khối lượng vật chất được giải phóng ở điện cực của bình điện phân tỉ lệ thuận với điện lượng chạy qua bình: \(m = kq\)
+ Định luật Faraday thứ hai: Đương lượng điện hóa k của một nguyên tố tỉ lệ với đương lượng gam \(\frac{A}{n}\) của nguyên tố đó. Hệ số tỉ lệ là \(\frac{1}{F}\) , trong đó F gọi là hằng số Fa-ra-day: \(k = \frac{1}{F}.\frac{A}{n}\)
Kết hợp hai định luật: \(m = \frac{1}{F}.\frac{A}{n}.It\)
Lời giải chi tiết:
Khối lượng của chất giải phóng ở điện cực được tính bằng công thức:
\(m = \frac{1}{F}.\frac{A}{n}.It\)
Mà đương lượng điện hóa \(k = \frac{1}{F}.\frac{A}{n}\)
\(m = k.It \Rightarrow k = \frac{m}{{I.t}}\)
Từ đồ thị ta có: \(t = 3phut = 180s \Rightarrow m = 2,{98.10^{ - 4}}kg\)
\( \Rightarrow k = \frac{m}{{I.t}} = \frac{{2,{{98.10}^{ - 4}}}}{{5.180}} = 3,{31.10^{ - 7}}\left( {Kg/C} \right)\)
Câu hỏi 26 :
Cho các khối lượng: hạt nhân \({}_{17}^{37}Cl\) ; nơtrôn; prôtôn lần lượt là 36,9566u; 1,0087u; 1,0073u. Độ hụt khối của hạt nhân \({}_{17}^{37}Cl\) bằng
- A 0,3278u
- B 0,3373u
- C 0,2927u
- D 0,3415u
Đáp án: D
Phương pháp giải:
Độ hụt khối: \(\Delta {m_X} = Z.{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
Lời giải chi tiết:
Độ hụt khối của hạt nhân \({}_{17}^{37}Cl\) bằng:
\(\begin{array}{l}\Delta {m_X} = Z.{m_p} + \left( {A - Z} \right){m_n} - {m_X}\\\,\,\,\,\,\,\,\,\,\,\, = 17.1,0073 + \left( {37 - 17} \right).1,0087 - 36,9566 = 0,3415u\end{array}\)
Câu hỏi 27 :
Xét mẫu nguyên tử Hidro của Bo, coi chuyển động của electron trên quỹ đạo dừng là chuyển động tròn đều. Tỉ số giữa tốc độ của electron trên quỹ đạo K và trên quỹ đạo M là
- A 9
- B 3
- C \(\frac{1}{3}\)
- D \(\frac{1}{9}\)
Đáp án: B
Phương pháp giải:
Công thức tính lực hướng tâm: \({F_{ht}} = \frac{{m{v^2}}}{r}\)
Biểu thức của định luật Culong: \(F = \frac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Khi electron chuyển động trên quỹ đạo dừng thì lực hút tĩnh điện đóng vai trò lực hướng tâm.
Lời giải chi tiết:
Công thức tính lực hướng tâm: \({F_{ht}} = \frac{{m{v^2}}}{r}\)
Biểu thức của định luật Culong: \(F = \frac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Khi electron chuyển động trên quỹ đạo dừng thì lực hút tĩnh điện đóng vai trò lực hướng tâm.
Ta có: \(k\frac{{\left| {{q_1}{q_2}} \right|}}{{r_n^2}} = \frac{{m{v^2}}}{{{r_n}}} \Rightarrow {v_n} = \sqrt {k.\frac{{\left| {{q_1}{q_2}} \right|}}{{m.{r_n}}}} \)
\( \Rightarrow \frac{{{v_K}}}{{{v_M}}} = \sqrt {\frac{{k.\frac{{\left| {{q_1}{q_2}} \right|}}{{m.{r_K}}}}}{{k.\frac{{\left| {{q_1}{q_2}} \right|}}{{m.{r_M}}}}}} = \sqrt {\frac{{{r_M}}}{{{r_K}}}} \)
Mặt khác bán kính quỹ đạo dừng được xác định là \({r_n} = {\rm{ }}{n^2}.{r_0}\)
Quỹ đạo K ứng với \(n = 1\); quỹ đạo M ứng với \(n = 3\)
Nên tỉ số \(\frac{{{v_L}}}{{{v_N}}} = \frac{{\sqrt {{3^2}.{r_0}} }}{{\sqrt {{1^2}.{r_0}} }} = 3\)
Câu hỏi 28 :
Poloni là một chất phóng xạ α có chu kì bán rã là 138 ngày. Một mẫu poloni nguyên chất lúc đầu có khối lượng 1g. Sau thời gian t, khối lượng poloni còn lại là 0,707g. Giá trị của t bằng
- A 97,57 ngày
- B 138 ngày
- C 69 ngày
- D 195,19 ngày
Đáp án: C
Phương pháp giải:
Khối lượng chất phóng xạ còn lại: \(m = {m_0}{.2^{ - \frac{t}{T}}}\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{m_0} = 1g\\m = 0,707g\\T = 138\,ngay\end{array} \right.\)
Khối lượng poloni còn lại được tính theo công thức:
\(\begin{array}{l}m = {m_0}{.2^{ - \frac{t}{T}}} \Rightarrow {2^{ - \frac{t}{{138}}}} = \frac{m}{{{m_0}}} = \frac{{0,707}}{1} \Rightarrow {2^{ - \frac{t}{{138}}}} \approx \frac{1}{{\sqrt 2 }}\\ \Rightarrow {2^{ - \frac{t}{{138}}}} = {2^{ - \frac{1}{2}}} \Rightarrow \frac{t}{{138}} = \frac{1}{2} \Rightarrow t = 69ngay\end{array}\)
Câu hỏi 29 :
Điện năng được truyền từ nhà máy điện bằng đường dây tải điện một pha có điện trở \(10\Omega \) . Biết công suất của nhà máy là 12MW, điện áp ở đầu đường truyền là 500kV, hệ số công suất bằng 1. Công suất hao phí trên đường dây tải điện là
- A 1736W
- B 5760W
- C 576kW
- D 57600W
Đáp án: B
Phương pháp giải:
Công thức tính công suất hao phí trên đường dây tải điện: \(\Delta P = \frac{{{P^2}R}}{{{U^2}.co{s^2}\varphi }}\)
Lời giải chi tiết:
Theo bài ra ta có: \(\left\{ \begin{array}{l}R = 10\Omega \\P = 12MW = {12.10^6}W\\U = 500kV = {500.10^3}V\\\cos \varphi = 1\end{array} \right.\)
Công suất hao phí trên đường dây tải điện là:
\(\Delta P = \frac{{{P^2}R}}{{{U^2}.co{s^2}\varphi }} = \frac{{{{\left( {{{12.10}^6}} \right)}^2}.10}}{{{{\left( {{{500.10}^3}} \right)}^2}.1}} = 5760W\)
Câu hỏi 30 :
Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm qua vị trí cân bằng thì tốc độ của nó là 20cm/s. Khi chất điểm có tốc độ là 10cm/s thì gia tốc của nó có độ lớn là \(40\sqrt 3 cm/s\). Biên độ của chất điểm bằng
- A 10cm
- B 5cm
- C \(5\sqrt 3 cm\)
- D \(10\sqrt 3 cm\)
Đáp án: B
Phương pháp giải:
Tại VTCB: \({v_{\max }} = \omega A\)
Hệ thức độc lập theo thời gian: \({A^2} = \dfrac{{{v^2}}}{{{\omega ^2}}} + \dfrac{{{a^2}}}{{{\omega ^4}}}\)
Lời giải chi tiết:
Khi chất điểm qua VTCB: \({v_{\max }} = \omega A \Rightarrow \omega = \frac{{{v_{\max }}}}{A} = \frac{{20}}{A}\)
Lại có: \({A^2} = \frac{{{v^2}}}{{{\omega ^2}}} + \frac{{{a^2}}}{{{\omega ^4}}} \Leftrightarrow {A^2}{\omega ^2} = {v^2} + \frac{{{a^2}}}{{{\omega ^2}}}\)
\(\begin{array}{l} \Leftrightarrow {A^2}.\frac{{{{20}^2}}}{{{A^2}}} = {10^2} + \frac{{{{\left( {40\sqrt 3 } \right)}^2}}}{{\frac{{{{20}^2}}}{{{A^2}}}}} \Leftrightarrow {20^2} = {10^2} + \frac{{{{\left( {40\sqrt 3 } \right)}^2}}}{{{{20}^2}}}.{A^2}\\ \Rightarrow {A^2} = 25 \Rightarrow A = 5cm\end{array}\)
Câu hỏi 31 :
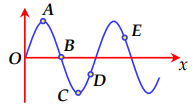
Trên một sợi dây rất dài dọc theo trục Ox đang có sóng cơ lan truyền ngược chiều dương của trục tọa độ. Hình dạng của một đoạn dây ở một thời điểm xác định có dạng như hình vẽ. Ngay sau thời điểm đó, nhận định đúng về chiều chuyển động của các điểm A, B, C, D và E là
- A Điểm C, D đi xuống và A, B, E đi lên
- B Điểm A, B, E đi xuống còn điểm C, D đi lên
- C Điểm B, C, E đi xuống còn A, D đi lên
- D Điểm A, D đi xuống còn B, C, E đi lên
Đáp án: B
Phương pháp giải:
Sử dụng hình vẽ:

Sườn đón sóng \( \Rightarrow \) các phần tử môi trường đi xuống.
Sườn không đón sóng \( \Rightarrow \) các phần tử môi trường đi lên.
Lời giải chi tiết:
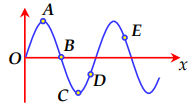
Sóng cơ lan truyền ngược chiều dương của trục tọa độ \( \Rightarrow \) Sóng truyền từ phải sang trái.
Điểm E, B nằm trên sườn đón sóng \( \Rightarrow E,B \downarrow \)
C ở đáy sóng \( \Rightarrow C \uparrow \)
A nằm ở đỉnh sóng \( \Rightarrow C \downarrow \)
D nằm ở sườn không đón sóng \( \Rightarrow D \uparrow \)
\( \Rightarrow \) Điểm A, B, E đi xuống còn điểm C, D đi lên
Câu hỏi 32 :
Một con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng bằng 100N/m và vật nhỏ khối lượng 250g. Từ vị trí cân bằng, kéo vật xuống dưới một đoạn sao cho lò xo dãn 7,5cm rồi thả nhẹ sau đó vật dao động điều hòa. Lấy \(g = 10m/{s^2}\). Tốc độ của vật khi nó đi qua vị trí lò xo không biến dạng là
- A 141,4 cm/s
- B 86,6 cm/s
- C 70,7 cm/s
- D 173,2 cm/s
Đáp án: B
Phương pháp giải:
Tần số góc: \(\omega = \sqrt {\frac{k}{m}} \)
Độ biến dạng tại VTCB: \(\Delta l = \frac{{mg}}{k}\)
Biên độ dao động: \(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} \)
Công thức tính tốc độ: \(v = \omega \sqrt {{A^2} - {x^2}} \)
Lời giải chi tiết:
Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{{0,25}}} = 20rad/s\)
Độ biến dạng của lò xo tại VTCB: \(\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{100}} = 2,5cm\)
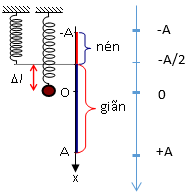
Từ VTCB kéo vật xuống dưới 1 đoạn sao cho lò xo dãn 7,5cm rồi thả nhẹ
\( \Rightarrow \Delta l + A = 7,5cm \Rightarrow A = 7,5 - 2,5 = 5cm\)
Vị trí lò xo không biến dạng có \(\left| x \right| = 2,5cm\)
\( \Rightarrow \) Tốc độ của vât khi nó đi qua vị trí lò xo không biến dạng là:
\(v = \omega \sqrt {{A^2} - {x^2}} = 20\sqrt {{5^2} - 2,{5^2}} = 86,6cm/s\)
Câu hỏi 33 :
Trên một sợi dây dài 2 m. Hai đầu cố định, đang có sóng dừng. Tốc độ truyền sóng trên dây là 20 m/s; tần số của sóng có giá trị trong khoảng từ 11 Hz đến 19 Hz. Nếu tính cả hai đầu dây thì số nút sóng trên dây là
- A 3
- B 2
- C 4
- D 5
Đáp án: C
Phương pháp giải:
Điều kiện có sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2} = k.\frac{v}{{2f}}\)
Trong đó: Số bụng sóng = k; Số nút sóng = k + 1.
Lời giải chi tiết:
Chiều dài sợi dây thỏa mãn: \(l = k.\frac{v}{{2f}} \Rightarrow f = \frac{{k.v}}{{2l}} = \frac{{k.20}}{{2.2}} = 5k\)
Mà \(11Hz < f < 19Hz \Leftrightarrow 11 < 5k < 19 \Rightarrow 2,2 < k < 3,8 \Rightarrow k = 3\)
\( \Rightarrow \) Số nút sóng = k + 1 = 3 + 1 = 4.
Câu hỏi 34 :
Đặt trước điện áp \(u = 100\sqrt 2 \cos \left( {100\pi t} \right)V\) vào hai đầu đoạn mach gồm điện trở thuần bằng \(100\Omega \), tụ điện có điện dung \(\frac{2}{\pi }{.10^{ - 4}}\left( F \right)\), cuộn cảm thuần có độ tự cảm \(\frac{3}{{2\pi }}\left( H \right)\) mắc nối tiếp. Biểu thức của cường độ dòng điện qua đoạn mạch là
- A \(i = \cos \left( {100\pi t - \frac{\pi }{4}} \right)A\)
- B \(i = 2\cos \left( {100\pi t + \frac{\pi }{4}} \right)A\)
- C \(i = \cos \left( {100\pi t + \frac{\pi }{4}} \right)A\)
- D \(i = 2\cos \left( {100\pi t - \frac{\pi }{4}} \right)A\)
Đáp án: A
Phương pháp giải:
Tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Cường độ dòng điện cực đại: \({I_0} = \frac{{{U_0}}}{Z}\)
Độ lệch pha giữa u và i: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Lời giải chi tiết:
Cảm kháng : \({Z_L} = \omega L = 100\pi .\frac{3}{{2\pi }} = 150\Omega \)
Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{2}{\pi }{{.10}^{ - 4}}}} = 50\Omega \)
Tổng trở: \(Z = \sqrt {{{100}^2} + {{\left( {150 - 50} \right)}^2}} = 100\sqrt 2 \Omega \)
Cường độ dòng điện cực đại: \({I_0} = \frac{{{U_0}}}{Z} = \frac{{100\sqrt 2 }}{{100\sqrt 2 }} = 1A\)
Độ lệch pha giữa u và i: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{150 - 50}}{{100}} = 1\)
\( \Rightarrow \varphi = \frac{\pi }{4} \Rightarrow {\varphi _u} - {\varphi _i} = \frac{\pi }{4} \Rightarrow {\varphi _i} = {\varphi _u} - \frac{\pi }{4} = 0 + \frac{\pi }{4} = - \frac{\pi }{4}\,\,\left( {rad} \right)\)
\( \Rightarrow i = \cos \left( {100\pi t - \frac{\pi }{4}} \right)A\)
Câu hỏi 35 :
Một dây dẫn thẳng, dài đặt trong chân không mang cường độ dòng điện không đổi. Cảm ứng từ tài điểm M cách dây một khoảng \({r_1}\) có độ lớn bằng \({B_1}\) . Cảm ứng từ tại N cách dây một khoảng \({r_2}\) có độ lớn bằng \({B_2}\). Cho biết \(2{B_2} = 3{B_1}\) và \(\left| {{r_1} - {r_2}} \right| = 3cm\). Giá trị của \({r_1}\) bằng
- A 6 cm
- B 2 cm
- C 3 cm
- D 9 cm
Đáp án: D
Phương pháp giải:
Cảm ứng từ do dòng điện chạy trong dây dẫn thẳng dài gây ra: \(B = {2.10^{ - 7}}.\frac{I}{r}\)
Lời giải chi tiết:
Có \(2{B_2} = 3{B_1} \Leftrightarrow 2.\frac{{{{2.10}^{ - 7}}.I}}{{{r_2}}} = 3.\frac{{{{2.10}^{ - 7}}.I}}{{{r_1}}} \Rightarrow 2{r_1} = 3{r_2}\,\,\left( 1 \right)\)
\( \Rightarrow {r_1} > {r_2} \Rightarrow \left| {{r_1} - {r_2}} \right| = {r_1} - {r_2} \Rightarrow {r_1} - {r_2} = 3cm\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}2{r_1} = 3{r_2}\,\\{r_1} - {r_2} = 3cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{r_1} = 9cm\\{r_2} = 6cm\end{array} \right.\)
Câu hỏi 36 :
Ở một nơi trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa. Gọi \({l_1},{s_{01}},{F_1}\) và \({l_2},{s_{02}},{F_2}\) lần lượt là chiều dài, biên độ, độ lớn lực kéo về cực đại của con lắc thứ nhất và của con lắc thứ hai. Biết \(3{l_2} = 2{l_1};2{s_{02}} = 3{s_{01}}\). Tỉ số \(\frac{{{F_1}}}{{{F_2}}}\) bằng
- A \(\frac{4}{9}\)
- B \(\frac{3}{2}\)
- C \(\frac{9}{4}\)
- D \(\frac{2}{3}\)
Đáp án: A
Phương pháp giải:
Độ lớn lực kéo về cực đại của con lắc đơn: \({F_{\max }} = m.{\omega ^2}.{S_0} = m.\frac{g}{l}.{S_0}\)
Lời giải chi tiết:
Ta có: \(\frac{{F_{1\max }^{}}}{{F_{2\max }^{}}} = \frac{{m\omega _1^2{S_{01}}}}{{m\omega _2^2{S_{02}}}} = \frac{{\frac{g}{{{\ell _1}}}.{S_{01}}}}{{\frac{g}{{{\ell _2}}}.{S_{02}}}} = \frac{{{S_{01}}.{\ell _2}}}{{{S_{02}}{\ell _1}}} = \frac{{{S_{01}}.\frac{{2{\ell _1}}}{3}}}{{\frac{{3{S_{01}}}}{2}{\ell _1}}} = \frac{4}{9}\)
Câu hỏi 37 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,2mm và khoảng cách từ hai khe đến màn là 1,8m. Ban đầu người ta sử dụng ánh sáng có bước sóng \({\lambda _1}\) thì hệ vân giao thoa thu được có khoảng vân 4,5mm. Nếu thay ánh sáng trên bằng ánh sáng có bước sóng \({\lambda _2} > {\lambda _1}\) thì tại vị trí vân sáng bậc 5 của ánh sáng có bước sóng \({\lambda _1}\) xuất hiện một vân sáng của ánh sáng có bước sóng \({\lambda _2}\). Biết rằng \(400nm < {\lambda _2} < 650nm\). Bước sóng \({\lambda _2}\) là
- A 600 nm.
- B 450 nm.
- C 500 nm.
- D 625 nm
Đáp án: D
Phương pháp giải:
Khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Vị trí vân sáng: \({x_s} = \frac{{k\lambda D}}{a} = k.i\)
Hai vân sáng trùng nhau có: \({k_1}{\lambda _1} = {k_2}{\lambda _2}\)
Lời giải chi tiết:
+ Ban đầu: \({i_1} = \frac{{{\lambda _1}D}}{a} \Rightarrow {\lambda _1} = \frac{{{i_1}.a}}{D} = \frac{{4,5.0,2}}{{1,8}} = 0,5\mu m = 500nm\)
+ Sau khi thay bằng bức xạ \({\lambda _2}\), tại vị trí vân sáng bậc 5 của ánh sáng có bước sóng \({\lambda _1}\) xuất hiện một vân sáng của ánh sáng có bước sóng \({\lambda _2}\)
\( \Rightarrow 5{\lambda _1} = k.{\lambda _2} \Rightarrow {\lambda _2} = \frac{{5{\lambda _1}}}{k} = \frac{{5.500}}{k} = \frac{{2500}}{k}\,\left( {nm} \right)\)
Mà \(400nm < {\lambda _2} < 650nm \Leftrightarrow 400 < \frac{{2500}}{k} < 650\)
\( \Leftrightarrow 3,8 < k < 6,25 \Rightarrow k = 4;5;6\)
Vì \({\lambda _2} > {\lambda _1} \Rightarrow k = 4 \Rightarrow {\lambda _2} = \frac{{2500}}{4} = 625\,\left( {nm} \right)\)
Câu hỏi 38 :
Trong hiện tượng giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp A, B cách nhau 20 cm dao động điều hòa theo phương thẳng đứng, cùng pha, cùng tần số 40 Hz. Tốc độ truyền sóng là 1,2 m/s. Ở bề mặt chất lỏng, xét đường tròn tâm A, bán kính AB, điểm nằm trên đường tròn dao động với biên độ cực đại cách đường trung trực của AB một đoạn lớn nhất là b. Giá trị của b gần nhất với giá trị nào sau đây ?
- A 28 cm.
- B 25 cm.
- C 5 cm.
- D 8 cm
Đáp án: B
Phương pháp giải:
Bước sóng: \(\lambda {\rm{}} = \frac{v}{f}\)
Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda \)
Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:
\( - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda }\)
Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với kmax.
Sử dụng định lí hàm số cos và các tỉ số lượng giác để tính toán.
Lời giải chi tiết:
Bước sóng: \(\lambda {\rm{}} = \frac{v}{f} = \frac{{120}}{{40}} = 3cm\)
Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:
\({ - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Leftrightarrow {\rm{}} - \frac{{20}}{3} < k < \frac{{20}}{3}}\)
\({ \Leftrightarrow {\rm{}} - 6,7 < k < 6,7 \Rightarrow k = {\rm{}} - 6; - 5;...;6}\)
Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với \({k_{max}} = 6\)
\({d_2} - {d_1} = {k_{\max }}\lambda {\rm{}} \Leftrightarrow MB - MA = 6.3 = 18cm\)
Mà \(MA = AB = 20cm \Rightarrow MB = 38cm\)
Ta có hình vẽ:
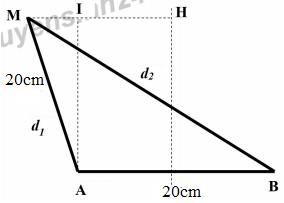
Áp dụng định lí hàm số cos trong tam giác MAB ta có:
\(\begin{array}{*{20}{l}}\begin{array}{l}M{B^2} = M{A^2} + A{B^2} - 2.MA.AB.cos\widehat {MAB}\\ \Rightarrow cos\widehat {MAB} = \frac{{M{A^2} + A{B^2} - M{B^2}}}{{2.MA.AB}} = \frac{{{{20}^2} + {{20}^2} - {{38}^2}}}{{2.20.20}}\\ \Rightarrow cos\widehat {MAB} = - 0,805 \Rightarrow \widehat {MAB} = 143,{6^0}\end{array}\\{ \Rightarrow \widehat {MAI} = \widehat {MAB} - {{90}^0} = 53,{6^0}}\\{ \Rightarrow MI = AB.\sin \widehat {MAI} = 20.0,805 = 16,1cm}\\{ \Rightarrow b = MH = MI + IH = 16,1 + 10 = 26,1cm}\end{array}\)
Câu hỏi 39 :
Một mạch điện gồm điện trở thuần R, cuộn cảm thuần có hệ số tự cảm L và tụ có điện dung C được mắc như hình vẽ.

Đặt vào hai điểm A, B của mạch điện trên một hiệu điện thế xoay chiều \(u = {U_0}\cos \omega t\)
• Khi nối Ampe kế lý tưởng vào M, N thì Ampe kế chỉ 0,1A. Dòng điện qua Ampe kế lệch pha với hiệu điện thế u là \(\frac{\pi }{6}\).
• Khi nối Vôn kế lý tưởng vào M, N thì Vôn kế chỉ 20V. Hiệu điện thế giữa hai đầu Vôn kế cũng lệch pha so với hiệu điện thế u là \(\frac{\pi }{6}\).
Giá trị của \(R,{\rm{ }}{Z_{L{\rm{ }}}},{Z_C}\) lần lượt là:
- A \(R = 150\Omega ;{Z_L} = 50\sqrt 3 \Omega ;{Z_C} = 200\sqrt 3 \Omega \)
- B \(R = 50\sqrt 3 \Omega ;{Z_L} = 200\sqrt 3 \Omega ;{Z_C} = 50\sqrt 3 \Omega \)
- C \(R = 50\Omega ;{Z_L} = 150\sqrt 3 \Omega ;{Z_C} = 200\sqrt 3 \Omega \)
- D \(R = 300\Omega ;{Z_L} = 100\sqrt 3 \Omega ;{Z_C} = 50\sqrt 3 \Omega \)
Đáp án: A
Phương pháp giải:
Độ lệch pha giữa u và i: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Biểu thức định luật Ôm: \(I = \frac{U}{Z}\)
Sử dụng giản đồ vecto và các hệ thức lượng trong tam giác vuông.
Lời giải chi tiết:
+ TH1: Khi nối ampe kế lí tưởng vào M, N \( \Rightarrow \) Tụ C bị nối tắt \( \Rightarrow \) Mạch gồm R,L.
u,i lệch pha \(\frac{\pi }{6}\) \( \Rightarrow \tan \frac{\pi }{6} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} \Rightarrow R = {Z_L}\sqrt 3 \,\,\,\left( 1 \right)\)

\( \Rightarrow Z = \frac{U}{I} = \frac{U}{{0,1}}\,\,\,\,\left( * \right)\)
+ TH2: Khi mắc vôn kế lí tưởng vào M,N \( \Rightarrow \) Mạch gồm R,L,C.
Vôn kế chỉ 20V \( \Rightarrow {U_C} = 20V\)
Ta có giản đồ vecto:
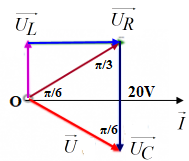
Từ giản đồ vecto ta \( \Rightarrow \widehat {{U_R}O{U_C}} = \frac{\pi }{2}\)
\( \Rightarrow U = {U_C}.\sin \widehat {O{U_R}{U_C}} = 20.\sin \frac{\pi }{3} = 10\sqrt 3 V\)
Thay \(U = 10\sqrt 3 V\) vào (*) ta được: \(Z = \frac{{10\sqrt 3 }}{{0,1}} = 100\sqrt 3 \Omega \)
\( \Rightarrow \sqrt {{R^2} + Z_L^2} = 100\sqrt 3 \,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}R = 150\Omega \\{Z_L} = 50\sqrt 3 \Omega \end{array} \right.\)
Câu hỏi 40 :
Một hệ gồm hai vật giống nhau có khối lượng \({m_1} = {m_2} = 200g\) dính với nhau bởi một lớp keo mỏng. Một lò xo có chiều dài tự nhiên là \({l_0} = 40cm\), treo thẳng đứng với đầu trên cố định, đầu dưới gắn vào \({m_1}\). Khi hệ vật cân bằng, lò xo dài 44cm. Lấy \(g = 10m/{s^2}\). Nâng hệ vật thẳng đứng đến khi lò xo có chiều dài 38 cm rồi thả nhẹ. Biết \({m_2}\) khi rời khỏi vật \({m_1}\) khi lực căng giữa chúng đạt tới 3,5N. Sau khi \({m_2}\) rời đi, biên độ dao động của vật \({m_1}\) gắn với giá trị
- A 4,7 cm.
- B 8,1 cm.
- C 6,2 cm.
- D 5,9 cm.
Đáp án: C
Phương pháp giải:
+ Độ biến dạng tại VTCB: \(\Delta l = \frac{{mg}}{k}\)
+ Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta l}}} \)
+ Công thức tính vận tốc: \(v = \pm \omega \sqrt {{A^2} - {x^2}} \)
+ Biên độ dao động: \(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} \)
+ Áp dụng biểu thức định luật II Niuton cho vật \({m_2}\) tại vị trí hai vật rời nhau.
Lời giải chi tiết:
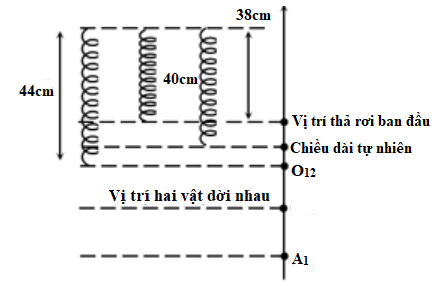
+ Hệ vật \(\left( {{m_1} + {m_2}} \right)\) dao động với:
\(\left\{ \begin{array}{l}\Delta {l_0} = 44 - 40 = 4cm\\A = 2 + 4 = 6cm\\\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{g}{{\Delta {l_{012}}}}} = \sqrt {\frac{{10}}{{0,04}}} = 5\pi \,rad/s\end{array} \right.\)
\( \Rightarrow k = \frac{{mg}}{{\Delta {l_{012}}}} = \frac{{0,4.10}}{{0,04}} = 100N/m\)
+ Áp dụng định luật II Niuton cho \({m_2}\) tại vị trí hai vật tách nhau:
\(\begin{array}{l}\overrightarrow {{P_2}} + \overrightarrow {{F_{12}}} = {m_2}\overrightarrow a \Leftrightarrow - {m_2}g + {F_{12}} = {m_2}a\\ \Leftrightarrow - {m_2}g + {F_{12}} = {m_2}.{\omega ^2}.\left| x \right|\\ \Leftrightarrow - 0,2.10 + 3,5 = 0,2.{\left( {5\pi } \right)^2}.\left| x \right| \Rightarrow \left| x \right| = 3cm\end{array}\)
\( \Rightarrow {v_{12}} = \omega \sqrt {{A^2} - {x^2}} = 5\pi \sqrt {{6^2} - {3^2}} = 81,6cm/s\)
+ Sau khi \({m_2}\) dời khỏi vật \({m_1}\) \( \Rightarrow {m_1}\) dao động điều hòa quanh vị trí cân bằng mới với:
\(\Delta {l_{01}} = \frac{{{m_1}g}}{k} = \frac{{0,2.10}}{{100}} = 0,02m = 2cm\)
\({\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,2}}} = 10\sqrt 5 rad/s\)
Tại vị trí \({m_2}\) hai vật tách nhau có:
\(\left\{ \begin{array}{l}
{x_1} = 2 + 3 = 5cm\\
{v_1} = {v_{12}} = 81,6cm/s
\end{array} \right.\)
\( \Rightarrow {A_1} = \sqrt {x_1^2 + \frac{{v_1^2}}{{\omega _1^2}}} = \sqrt {{5^2} + {{\left( {\frac{{81,6}}{{10\sqrt 5 }}} \right)}^2}} = 6,2cm\)
