Câu hỏi 1 :
Bản chất của tia phóng xạ \(\alpha \) là
- A dòng các hạt nhân \(_2^4He\)
- B dòng các pôzitron.
- C Bức xạ điện từ.
- D dòng các electron.
Đáp án: A
Phương pháp giải:
Sử dụng lí thuyết về các tia phóng xạ:
Các tia phóng xạ thường được đi kèm trong sự phóng xạ của các hạt nhân. Có 3 loại tia phóng xạ chính có bản chất khác nhau là tia anpha (ký hiệu là \(\alpha \)), tia beta (kí hiệu là \(\beta \)), tia gamma (kí hiệu là \(\gamma \)).
Lời giải chi tiết:
- Tia \(\alpha \) thực chất hạt nhân của nguyên tử Heli, kí hiệu là \({}_2^4He.\)
- Tia \(\beta \) (bao gồm \({\beta ^ + }\) và \({\beta ^ - }\)) là các hạt phóng xạ với tốc độ lớn, làm ion hoá không khí và yếu hơn tia \(\alpha .\)
- Tia \(\gamma \) là sóng điện từ có bước sóng rất ngắn, cũng là hạt phôtôn có năng lượng cao, thường đi kèm trong các phóng xạ \({\beta ^ + }\) và \({\beta ^ - }\)
Câu hỏi 2 :
Đặt điện áp xoay vào hai đầu đoạn mạch gồm điện trở thuần \(R = 40\Omega \) mắc nối tiếp với tụ điện thì dung kháng của tụ điện là \({Z_C} = 60\Omega \). Tổng trở của đoạn mạch là
- A \(Z = 100\Omega \)
- B \(Z = 20\sqrt 5 \Omega \)
- C \(Z = 20\sqrt {13} \Omega \)
- D \(Z = 20\Omega \).
Đáp án: C
Phương pháp giải:
Áp dụng công thức tính tổng trở của mạch gồm \(R\) và \({Z_C}\): \(Z = \sqrt {{R^2} + Z_C^2} \)
Lời giải chi tiết:
Tổng trở của đoạn mạch là: \(Z = \sqrt {{R^2} + Z_C^2} = \sqrt {{{40}^2} + {{60}^2}} = 20\sqrt {13} \left( \Omega \right)\)
Câu hỏi 3 :
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo, mức năng lượng của nó ở các trạng thái dừng theo thứ tự tăng dần từ giá trị nhỏ nhất là \({E_1},{E_2},{E_3} \ldots \) Nguyên tử hiđrô hấp thụ một phôtôn có năng lượng \(\varepsilon = {E_3} - {E_1}\) thì êlectron chuyển từ quỹ đạo
- A \(N\) đến quỹ đạo \(L\).
- B \(M\) đến quỹ đạo \(K.\)
- C \(L\) đến quỹ đạo \(N.\)
- D \(K\) đến quỹ đạo \(M.\)
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết tiên đề về trạng thái dừng:
Nguyên tử chỉ tồn tại trong một số trạng thái có năng lượng xác định \({E_n}\), gọi là các trạng thái dừng. Khi ở trạng thái dừng, nguyên tử không bức xạ.
Bình thường nguyên tử ở trạng thái dừng có năng lượng thấp nhất gọi là trạng thái cơ bản \(n = 1.\) Khi hấp thụ năng lượng thì nguyên tử ở các trạng thái dừng có năng lượng cao hơn gọi là trạng thái kích thích thứ \(n\left( {n > 1} \right).\)
Tên của các quỹ đạo dừng: \(K,{\rm{ }}L,{\rm{ }}M,{\rm{ }}N,{\rm{ }}O{\rm{ }} \ldots .\)
Lời giải chi tiết:
Các mức năng lượng \({E_1},\,\,{E_2},\,\,{E_3}\) tương ứng với các trạng thái dừng trên các quỹ đạo \(K,\,\,L,\,\,M.\)
Vậy khi nguyên tử hiđrô hấp thụ một phôtôn có năng lượng \(\varepsilon = {E_3} - {E_1}\) thì êlectron chuyển từ quỹ đạo \(K\) lên quỹ đạo \(M.\)
Câu hỏi 4 :
Một sóng ngang truyền trên sợi dây rất dài với phương trình sóng \(u = A\cos \left( {20\pi t - \frac{\pi }{{10}}x} \right)\) (\(x\) tính bằng \({\rm{cm}},t\) tính bằng \({\rm{s}})\). Bước sóng trên sợi dây là
- A \(\lambda = 10\;cm\)
- B \(\lambda = 20cm.\)
- C \(\lambda = 20\pi \,cm.\)
- D \(\lambda = 10\pi cm.\)
Đáp án: B
Phương pháp giải:
Phương trình sóng tổng quát: \(u = A\cos \left( {\omega t - \frac{{2\pi x}}{\lambda }} \right)\)
Lời giải chi tiết:
Đối chiếu phương trình sóng với phương trình tổng quát, ta có:
\(\frac{{2\pi x}}{\lambda } = \frac{\pi }{{10}}x \Rightarrow \lambda = 20\,\left( {cm} \right)\)
Câu hỏi 5 :
Giới hạn quang điện của kim loại đồng là \(0,3\mu m\). Chiếu lần lượt các bức xạ có bước sóng (trong chân không) là \(0,50\mu m;\,\,0,28\mu m;\,\,0,35\mu m;\,\,0,41\mu m\) và \(0,19\mu m\) vào một tấm đồng. Số bức xạ gây ra được hiện tượng quang điện ngoài là
- A \(4.\)
- B \(2.\)
- C \(3\)
- D \(1.\)
Đáp án: B
Phương pháp giải:
Để xảy ra hiện tượng quang điện thì \(\lambda \le {\lambda _0}\) với \({\lambda _0}\) là giới hạn quang điện của kim loại, \(\lambda \) là bước sóng của ánh sáng kích thích.
Lời giải chi tiết:
Để xảy ra hiện tượng quang điện thì \(\lambda \le {\lambda _0} = 0,3\mu m \Rightarrow \lambda = 0,19\,\,\mu m\) và \(\lambda = 0,28\,\,\mu m\)
Câu hỏi 6 :
Khoảng cách từ đài truyền hình Việt Nam (VTV) đến vệ tinh VINASAT-2 khoảng \(36.000\;{\rm{km}}\). Cho \(c = {3.10^8}\;m/s\). Thời gian để sóng vô tuyến truyền từ đài VTV đến vệ tinh có giá trị là
- A \(0,18\;{\rm{s}}\).
- B \(0,24\;{\rm{s}}\)
- C \(0,06\,{\rm{s}}{\rm{.}}\)
- D \(0,12\,{\rm{s}}{\rm{.}}\)
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính thời gian: \(t = \frac{s}{v}.\)
Lời giải chi tiết:
Thời gian để sóng vô tuyến truyền từ đài VTV đến vệ tinh VINASAT-2 là:
\(t = \frac{s}{v} = \frac{{36000.1000}}{{{{3.10}^8}}} = 0,12s\)
Câu hỏi 7 :
Cấu tạo của buồng tối trong máy quang phổ lăng kính gồm
- A một (hoặc hai, ba) lăng kính làm nhiệm vụ tán sắc ánh sáng.
- B một hay nhiều lăng kính đặt song song nhau.
- C một thấu kính hội tụ và một khe hẹp tại tiêu điểm chính.
- D một thấu kính hội tụ và một tấm phim đặt ở tiêu diện.
Đáp án: D
Phương pháp giải:
Ống chuẩn trực: Một đầu là TKHT L1, đầu còn lại có 1 khe hẹp F nằm ở tiêu diện TKHT L1 để cho chùm tia ló song song.
Hệ tán sắc: Gồm 1 hoặc vài lăng kính P để phân tích chùm ánh sáng song song thành các chùm ánh sáng đơn sắc song song.
Buồng ảnh: Là một hộp kín, một đầu là thấu kính hội tụ L2 (nằm sau lăng kính) đầu còn lại là kính ảnh đặt tại tiêu diện của L2. Chùm ánh sáng đơn sắc song song khi vào buồng ảnh tạo thành nhiều ảnh của nguồn sáng, mỗi ảnh ứng với một bước sóng xác định gọi là vạch quang phổ.
Lời giải chi tiết:
Cấu tạo của buồng tối trong máy quang phổ lăng kính gồm một thấu kính hội tụ và một tấm phim đặt ở tiêu diện.
Câu hỏi 8 :
Một chùm ánh sáng đơn sắc đỏ truyền trong chân không có bước sóng \(\lambda = 0,75\mu m\). Cho hằng số Plăng là \(h = 6,{625.10^{ - 34}}\;J.s;\,\,c = {3.10^8}\;m/s\). Năng lượng phôtôn của ánh sáng là
- A \(\varepsilon = 2,{34.10^{ - 19}}\;{\rm{J}}\)
- B \(\varepsilon = 1,{66.10^{ - 19}}\;{\rm{J}}\)
- C \(\varepsilon = 2,{65.10^{ - 19}}\;{\rm{J}}\)
- D \(\varepsilon = 2,{15.10^{ - 19}}\;{\rm{J}}\)
Đáp án: C
Phương pháp giải:
Áp dụng công thức: \(\varepsilon = \frac{{hc}}{\lambda }\)
Lời giải chi tiết:
Năng lượng phôtôn của ánh sáng là:
\(\varepsilon = \frac{{hc}}{\lambda } = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{0,{{75.10}^{ - 6}}}} = 2,{65.10^{ - 19}}\left( J \right)\)
Câu hỏi 9 :
Nguyên tắc hoạt động của máy phát điện xoay chiều ba pha dựa trên hiện tượng
- A cộng hưởng điện.
- B quang điện trong.
- C cảm ứng điện từ.
- D giao thoa sóng điện từ.
Đáp án: C
Phương pháp giải:
Sử dụng lí thuyết cấu tạo và hoạt động của máy phát điện xoay chiều ba pha.
Lời giải chi tiết:
Máy phát điện xoay chiều ba pha hoạt động dựa trên hiện tượng cảm ứng điện từ.
Câu hỏi 10 :
Một điện tích điểm \(q\) đặt ở điểm \(O\) trong chân không, tại điểm \(M\) cách \(O\) một đoạn \(r\) thì cường độ điện trường có độ lớn
- A tỉ lệ thuận với \(r\).
- B tỉ lệ nghịch với \({r^2}.\)
- C tỉ lệ nghịch với \(r.\)
- D tỉ lệ thuận với \({r^2}.\)
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính cường độ điện trường do điện tích điểm gây ra: \(E = k\frac{{\left| q \right|}}{{{r^2}}}\)
Lời giải chi tiết:
Cường độ điện trường tại M là: \(E = k\frac{{\left| q \right|}}{{O{M^2}}} = k\frac{{\left| q \right|}}{{{r^2}}} \Rightarrow E \sim \frac{1}{{{r^2}}}\)
Câu hỏi 11 :
Đặt điện áp xoay chiều vào hai đầu cuộn thuần cảm thì cường độ dòng điện chạy qua cuộn cảm
- A lệch pha \(\frac{\pi }{2}\) so với điện áp.
- B lệch pha \(\frac{\pi }{4}\) so với điện áp.
- C cùng pha với điện áp.
- D ngược pha so với điện áp.
Đáp án: A
Phương pháp giải:
Sử dụng lí thuyết mạch chỉ chứa 1 phần tử \(R,\,L,\,\)hoặc \(C.\)
Lời giải chi tiết:
- Mạch chứa \(R:\) dòng điện cùng pha điện áp.
- Mạch chứa \(L:\) dòng điện trễ pha \(\frac{\pi }{2}\) so với điện áp.
- Mạch chứa \(C:\) dòng điện sớm pha \(\frac{\pi }{2}\) so với điện áp.
Câu hỏi 12 :
Dòng điện trong chất điện phân là dòng chuyển động có hướng
- A của các lỗ trống cùng chiều điện trường.
- B của electron và lỗ trống theo hai chiều ngược nhau.
- C của ion âm và ion dương theo hai chiều ngược nhau.
- D của các electron ngược chiều điện trường.
Đáp án: C
Phương pháp giải:
Sử dụng lí thuyết dòng điện trong chất điện phân.
Lời giải chi tiết:
Dòng điện trong chất điện phân là dòng chuyển dịch có hướng của các ion dương về catôt và ion âm về anot.
Câu hỏi 13 :
Trong thí nghiệm giao thoa sóng ở mặt nước với hai nguồn kết hợp cùng pha, các vân giao thoa cực tiểu là những đường
- A tròn.
- B parabol.
- C thẳng
- D hypebol
Đáp án: D
Phương pháp giải:
Trong thí nghiệm giao thoa sóng sẽ tạo ra những điểm cực đại và cực tiểu. Quỹ tích các điểm dao động với biên độ cực đại hoặc các điểm dao động với biên độ cực tiểu tạo thành một họ các đường hyperbol với tiêu điểm là 2 nguồn \({S_1}\) và \({S_2}.\)
Lời giải chi tiết:
Trong giao thoa sóng mặt nước, các vân giao thoa cực tiểu là những đường hypebol.
Câu hỏi 14 :
Chức năng khuếch đại âm của hộp đàn ghita là dựa trên hiện tượng
- A phản xạ âm.
- B dao động tắt dần.
- C cộng hưởng âm.
- D nhiễu xạ âm.
Đáp án: C
Phương pháp giải:
Sử dụng lí thuyết về hộp cộng hưởng.
Lời giải chi tiết:
Mỗi cây đàn dây thường có dây được căng trên một hộp đàn có hình dạng và kích thước khác nhau. Hộp đàn có tác dụng như một hộp cộng hưởng sẽ tăng cường âm cơ bản và một số hoạ âm giúp cho âm tổng hợp phát ra vừa to vừa có một âm sắc riêng của đàn.
Câu hỏi 15 :
Hai dao động điều hoà cùng phương, cùng tần số, cùng pha thì có độ lệch pha bằng
- A \(2k\pi \) với \(k = 0, \pm 1, \pm 2, \ldots \)
- B \(\left( {2k + 0,5} \right)\pi \) với \(k = 0, \pm 1, \pm 2, \ldots \)
- C \(\left( {k + 0,5} \right)\pi \) với \(k = 0, \pm 1, \pm 2, \ldots \)
- D \(\left( {2k + 1} \right)\pi \) với \(k = 0, \pm 1, \pm 2...\)
Đáp án: A
Phương pháp giải:
Độ lệch pha: \(\Delta \varphi = \left| {{\varphi _1} - {\varphi _2}} \right|\)
Lời giải chi tiết:
Hai dao động điều hoà cùng phương, cùng tần số, cùng pha thì có độ lệch pha bằng \(\Delta \varphi = 2k\pi \) với \(k = 0,1,\,2...\)
Câu hỏi 16 :
Một con lắc lò xo có độ cứng \(k\), khối lượng vật nhỏ \(m\) dao động điều hoà. Tại thời điểm mà li độ và vận tốc của vật tương ứng là \(x\) và \(v\) thì động năng của vật là
- A \({W_d} = \frac{1}{2}m{x^2}\)
- B \({W_d} = \frac{1}{2}k{x^2}\)
- C \({W_d} = \frac{1}{2}m{v^2}.\)
- D \({W_d} = \frac{1}{2}k{v^2}\)
Đáp án: C
Phương pháp giải:
Công thức tính động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}.\)
Lời giải chi tiết:
Động năng của vật là:\({{\rm{W}}_d} = \frac{1}{2}m{v^2}.\)
Câu hỏi 17 :
Bước sóng của một sóng hình sin là quãng đường sóng truyền được trong
- A hai giây.
- B một giây.
- C hai chu kì.
- D một chu kì.
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết khái niệm bước sóng.
Lời giải chi tiết:
Bước sóng là quãng đường sóng truyền đường trong một chu kì.
Câu hỏi 18 :
Đặt khung dây dẫn phẳng, kín với diện tích \(S\) trong từ trường đều có cảm ứng từ \(B.\) Từ thông qua khung dây có độ lớn là \(\Phi = 0,8BS\). Góc giữa vectơ pháp tuyến của mặt phẳng khung dây với đường sức từ là
- A 0,644 rad
- B \(0,800\,{\rm{rad}}{\rm{.}}\)
- C \(0,721\,{\rm{rad}}{\rm{.}}\)
- D 0,927 rad.
Đáp án: A
Phương pháp giải:
Công thức tính từ thông: \(\Phi = NBS\cos \alpha \)
Lời giải chi tiết:
Ta có: \(\Phi = NBS\cos \alpha = 0,8BS\) (mà \(N = 1\))
\( \Rightarrow \cos \alpha = 0,8 \Rightarrow \alpha = \left( {\overrightarrow B ,\overrightarrow n } \right) = 36^\circ 52' = 0,644\left( {rad} \right)\)
Câu hỏi 19 :
Đặc trưng nào sau đây không phải là đặc trưng sinh lí của âm?
- A Mức cường độ âm.
- B Độ to của âm.
- C Độ cao của âm.
- D Âm sắc.
Đáp án: A
Phương pháp giải:
Các đặc trưng sinh lí của âm là: độ cao, độ to, âm sắc.
Lời giải chi tiết:
Mức cường độ âm là đặc trưng vật lí.
Câu hỏi 20 :
Đặt vào hai đầu điện trở \(R\) một hiệu điện thế không đổi \(U\). Công suất toả nhiệt trên điện trở \(R\) là
- A \(P = \frac{U}{R}\).
- B \(P = UR\).
- C \(P = \frac{{{U^2}}}{R}\).
- D \(P = {U^2}R\)
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính công suất toả nhiệt: \(P = \frac{{{U^2}}}{R}\)
Lời giải chi tiết:
Công suất toả nhiệt trên \(R:\,\,P = {I^2}R = \frac{{{U^2}}}{R}.\)
Câu hỏi 21 :
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu mạch điện \(R,\,\,L,\,C\) mắc nối tiếp thì xảy ra cộng hưởng điện. Tổng trở của đoạn mạch lúc này bằng giá trị của
- A điện dung.
- B dung kháng.
- C điện trở.
- D cảm kháng.
Đáp án: C
Phương pháp giải:
Tổng trở đoạn mạch xoay chiều: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Khi mạch điện xoay chiều xảy ra cộng hường thì \({Z_L} = {Z_C}.\)
Lời giải chi tiết:
Khi có cộng hưởng thì \({Z_L} = {Z_C} \Rightarrow Z = R\)
Câu hỏi 22 :
Tia phóng xạ nào sau đây không bị lệch trong điện trường?
- A
Tia \(\alpha \)
- B
Tia \({\beta ^ + }\)
- C
Tia \({\beta ^ - }\)
- D
Tia \(\gamma \)
Đáp án: D
Lời giải chi tiết:
Tia \(\gamma \) không bị lệch trong điện trường
Câu hỏi 23 :
Trong sơ đồ khối của một máy thu thanh vô tuyến đơn giản, mạch khuếch đại có tác dụng
- A tăng cường tần số dao động cao tần.
- B tăng cường tần số dao động âm tần.
- C tăng cường biên độ dao động cao tần.
- D tăng cường biên độ dao động âm tần.
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết về cấu tạo và chức năng của các bộ phận trong sơ đồ khối của máy thu vô tuyến.
Lời giải chi tiết:
Sơ đồ máy thu thanh gồm có:
Anten thu: Có thể thu được tất cả sóng điện từ truyền tới nó.
Mạch khuếch đại dao động điện từ cao tần: Làm cho sóng điện từ cao tần thu được có năng lượng (biên độ) lớn hơn.
Mạch tách sóng: Tách sóng âm tần ra khỏi sóng mang.
Mạch khuếch đại dao động điện từ âm tần: Làm cho dao động âm tần vừa tách ra có năng lượng (biên độ) lớn hơn.
Loa: Biến dao động điện âm tần thành âm thanh (tái tạo âm thanh).
Câu hỏi 24 :
Hạt nhân Đơteri \({}_1^2D\) có khối lượng \(2,0136{\rm{ }}u.\) Biết khối lượng của prôtôn là \(1,0073u\) và khối lượng của nơtrôn là \(1,0087{\rm{ }}u.\) Độ hụt khối của hạt nhân \({}_1^2D\) bằng
- A \(0,0024u\).
- B \(0,0012u.\)
- C \(0,0032u.\)
- D \(0,0036u.\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính độ hụt khối: \(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}.\)
Lời giải chi tiết:
Độ hụt khối của hạt nhân \({}_1^2D\) là:
\(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
\( = 1,0073u + (2 - 1).1,0087u - 2,0136u\)
\( = 0,0024u\)
Câu hỏi 25 :
Tính chất nổi bật và quan trọng nhất của tia \(X\) là
- A ion hoá không khí.
- B khả năng đâm xuyên.
- C làm đen kính ảnh.
- D tác dụng sinh lí.
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết tia \(X.\)
Lời giải chi tiết:
- Tính chất nổi bật của tia \(X\) là khả năng đâm xuyên tốt: truyền qua được những vật chắn sáng thông thường như giấy, gỗ, hay kim loại mỏng … Bước sóng càng ngắn, đâm xuyên càng mạnh. Ngoài ra còn một số tính chất:
- Tác dụng rất mạnh lên kính ảnh.
- Làm phát quang một số chất.
- Có khả năng ion hóa không khí và các chất khí.
- Tác dụng sinh học rất mạnh: hủy hoại tế bào, diệt vi khuẩn, …
Câu hỏi 26 :
Một máy phát điện xoay chiều một pha có rô to là phần cảm gồm có 4 cặp cực quay với tốc độ \(12,5\)vòng/s. Tần số của suất điện động do máy phát sinh ra là:
- A \(f = 50\pi Hz.\)
- B \(f = 100Hz.\)
- C \(f = 25Hz.\)
- D \(f = 50Hz.\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức \(f = p.n\) với \(n\) là tốc độ quay của rô to, \(p\) là số cặp cực.
Lời giải chi tiết:
Tần số của suất điện động do máy phát sinh ra là:
\(f = p.n = 4.12,5 = 50\left( {Hz} \right)\)
Câu hỏi 27 :
Khi chiếu ánh sáng có bước sóng thích hợp vào một chất thì điện trở suất của nó giảm. Chất này được gọi là
- A chất phát quang.
- B kim loại.
- C điện môi.
- D chất quang dẫn.
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết chất quang dẫn.
Lời giải chi tiết:
Khi chiếu ánh sáng thích hợp vào các chất quang dẫn → điện trở của nó giảm → cho dòng điện chạy qua.
Câu hỏi 28 :
Một con lắc đơn có chiều dài \(l = 80\,\,cm\) dao động điều hòa tại nơi có \(g = 9,81\;m/{s^2}\). Chu kỳ dao động của con lắc là
- A \(1,242s.\)
- B \(1,793s.\)
- C \(0,558s.\)
- D \(2,351s.\)
Đáp án: B
Phương pháp giải:
Áp dụng công thức: \(T = 2\pi \sqrt {\frac{l}{g}} .\)
Lời giải chi tiết:
Chu kỳ dao động của con lắc là:
\(T = 2\pi \sqrt {\frac{l}{g}} = 2\pi \sqrt {\frac{{0,8}}{{9,81}}} \approx 1,793\left( s \right)\)
Câu hỏi 29 :
Cho hạt nhân nguyên tử \({}_Z^AX\). Số nơtron trong hạt nhân nguyên tử bằng
- A
A
- B
Z
- C
A – Z
- D
A + Z
Đáp án: C
Phương pháp giải:
Xem lại lí thuyết mục 1 (cấu tạo hạt nhân)
Lời giải chi tiết:
Ta có: A = số proton + số nơtron = Z + N => N = A - Z
Câu hỏi 30 :
Phản ứng nhiệt hạch là phản ứng trong đó
- A các nuclôn kết hợp thành một hạt nhân bền.
- B hai hạt nhân nhẹ tổng hợp thành một hạt nhân nặng hơn.
- C một hạt nhân nặng vỡ thành các mảnh nhẹ hơn.
- D một hạt nhân không bền phân rã tự phát và toả nhiệt.
Đáp án: B
Phương pháp giải:
Sử dụng định nghĩa phản ứng nhiệt hạch.
Lời giải chi tiết:
Phản ứng nhiệt hạch: là phản ứng trong đó 2 hay nhiều hạt nhân nhẹ tổng hợp lại thành một hạt nhân nặng hơn và vài nơtron.
Câu hỏi 31 :
Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có đồ thị li độ của các dao động thành phần theo thời gian như hình vẽ. Khi đi qua vị trí cân bằng, vật có tốc độ là
- A \(32\pi {\rm{cm}}/{\rm{s}}\)
- B \(28\;{\rm{cm}}/{\rm{s}}\)
- C \(32\;{\rm{cm}}/{\rm{s}}\)
- D \(28\pi {\rm{cm}}/{\rm{s}}\)
Đáp án: D
Phương pháp giải:
Dựa vào đồ thị suy ra các đại lượng \({A_1},\,\,{A_2},\,\,\omega ,\,\,{\varphi _1},\,{\varphi _2}\) của hai dao động và tổng hợp hai dao động đó.
Áp dụng công thức \({v_{\max }} = \omega A\) với \(A\) là biên độ tổng hợp.
Lời giải chi tiết:
Từ hình vẽ: \(\frac{T}{2} = 0,5s \Rightarrow T = 1\left( s \right)\)
Tần số góc của hai dao động là:
\(\omega = \frac{{2\pi }}{T} = 2\pi \left( {rad/s} \right)\)
Biên độ của hai dao động: \({A_1} = 10cm,\,\,{A_2} = 6\,cm.\)
Lúc \(t = 0,\,\left\{ \begin{array}{l}{x_2} = 6cm = {A_1} \Rightarrow {\varphi _1} = 0\\\left\{ \begin{array}{l}{x_1} = 5cm = \frac{{{A_1}}}{2}\\{v_1} < 0\end{array} \right. \Rightarrow {\varphi _2} = \frac{\pi }{3}\end{array} \right.\)
Phương trình dao động của hai vật là:
\(\left\{ \begin{array}{l}{x_1} = 10\cos \left( {2\pi t + \frac{\pi }{3}} \right)\\{x_2} = 6\cos \left( {2\pi t} \right)\end{array} \right.\)
Biên độ dao động tổng hợp là:
\(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \left( {\overrightarrow {{A_1}} ,\overrightarrow {{A_2}} } \right)} \\ \Rightarrow A = \sqrt {{{10}^2} + {6^2} + 2.10.6.\cos \frac{\pi }{3}} = 14\left( {cm} \right)\end{array}\)
Khi đi qua vị trí cân bằng, vật có tốc độ là:
\({v_{\max }} = \omega A = 2\pi .14 = 28\pi \)(cm/s)
Câu hỏi 32 :
Đặt điện áp \(u = 6\sqrt 2 \cos \left( {\omega t} \right)\,\,V\) (\(\omega \) không đổi) vào hai đầu đoạn mạch gồm cuộn dây mắc nối tiếp với tụ điện. Điện áp hiệu dụng hai đầu cuộn dây là \(10\;{\rm{V}}\) và sớm pha hơn điện áp hai đầu mạch là \(1,56{\rm{rad}}.\)Hệ số công suất của mạch là
- A \(0,40.\)
- B \(0,52\).
- C \(0,60.\)
- D \(0,86.\)
Đáp án: D
Phương pháp giải:
Vì độ lệch pha giữa \({u_d}\) và \(u\) là 1,56rad nên cuộn dây có điện trở thuần.
Sử dụng giản đồ vecto.
Lời giải chi tiết:
Ta có: \(\left( {{u_d},u} \right) = 1,56rad = \frac{\pi }{2};U = 6V;{U_d} = 10V\)
Vì điện áp hai đầu cuộn dây lệch pha với điện áp hai đầu đoạn mạch góc 1,56rad nên cuộn dây có điện trở thuần.
Ta có giản đồ vecto:
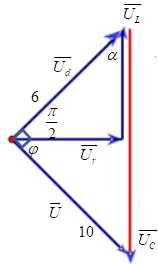
Từ giản đồ vecto ta có: \(\tan \alpha = \frac{6}{{10}} = 0,6\)
\( \Rightarrow \alpha = shif\tan 0,6 = 0,54042\) \( \Rightarrow \cos \alpha = 0,86\)
Mà \(\alpha = \varphi \Rightarrow \cos \varphi = 0,86\)
Câu hỏi 33 :
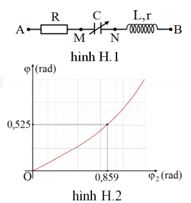
Đặt điện áp xoay chiều (có giá trị hiệu dụng và tần số không đổi) vào hai đầu đoạn mạch như hình H.1 thì cảm kháng của cuộn dây \({Z_L} = 2r\). Gọi \(\varphi \) và \({\varphi _2}\) tương ứng là độ lệch pha giữa điện áp \({u_{AB}}\) và \({u_{MB}}\) so với cường độ dòng điện trong mạch. Đồ thị biểu diễn sự phụ thuộc của \(\varphi \) vào \({\varphi _2}\) khi điện dung \(C\) thay đổi như hình H.2. Khi \(C = {C_0}\) thì điện áp \({u_{AN}}\) lệch pha \({90^0}\) so với \({u_{MB}}\). Khi đó, hệ số công suất của đoạn mạch \(MB\) là
- A \(0,46.\)
- B \(0,71.\)
- C \(0,87.\)
- D \(0,89.\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính \(\tan \varphi \) cho đoạn mạch \(AB\) và \(MB.\)
Dựa vào \({u_{AN}} \bot {u_{MB}} \Rightarrow \frac{{{Z_{{C_0}}}}}{R}.\frac{{{Z_L} - {Z_{{C_0}}}}}{r} = 1\) → \({Z_{{C_0}}}\) → \(\cos {\varphi _{MB}}.\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\tan \varphi = \frac{{{Z_{LC}}}}{{R + r}} = \tan 0,525\\\tan {\varphi _2} = \frac{{{Z_{LC}}}}{r} = \tan 0,859\end{array} \right. \Rightarrow \frac{{R + r}}{r} = 2 \Rightarrow R = r\)
Lấy \(R = 1 = r \Rightarrow {Z_L} = 2\)
Theo bài ta có: \({u_{AN}} \bot {u_{MB}} \Rightarrow \frac{{{Z_{{C_0}}}}}{R}.\frac{{{Z_L} - {Z_{{C_0}}}}}{r} = 1 \Rightarrow {Z_{{C_0}}} = 1.\)
Hệ số công suất của đoạn mạch \(MB\) là:
\(\cos {\varphi _{MB}} = \frac{r}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_{{C_0}}}} \right)}^2}} }} = \frac{1}{{\sqrt 2 }} = 0,71.\)
Câu hỏi 34 :
Một vật dao động điều hoà với phương trình \(x = 6\cos \left( {2\pi t + \frac{\pi }{6}} \right){\rm{cm}}.\) Trên vật gắn với một nguồn sáng phát ánh sáng đơn sắc có tần số \({5.10^{14}}\) Hz, công suất \(0,53\)W. Biết hằng số Plăng là \(h = 6,{625.10^{ - 34}}\;{\rm{J}}{\rm{.s}}\)Tính từ thời điểm \(t = 0\) đến thời điểm gần nhất vật có li độ \( - 3\;{\rm{cm}}\) thì nguồn sáng phát số phôtôn gần nhất với giá trị nào sau đây?
- A \({4.10^{17}}\) hạt.
- B \({8.10^{17}}\) hạt.
- C \({5.10^{18}}\) hạt.
- D \(1,{6.10^{18}}\) hạt.
Đáp án: A
Phương pháp giải:
Áp dụng công thức: \(n = \frac{P}{{hf}}.\Delta t\) với \(P\) là công suất nguồn phát, \(\Delta t\) là thời gian.
Lời giải chi tiết:
Lúc \(t = 0,\left\{ \begin{array}{l}x = 3\sqrt 3 cm\\v < 0\end{array} \right.\)
Từ \(t = 0\) đến thời điểm gần nhất vật có li độ: \(\left\{ \begin{array}{l}x = - 3cm\\v < 0\end{array} \right.\)
Khoảng thời gian vật đã đi được là: \(\frac{T}{6} + \frac{T}{{12}} = \frac{T}{4} = 0,25\left( s \right)\)
Số phôtôn gần nhất mà nguồn sáng phát ra là:
\(n = \frac{P}{{hf}}.\Delta t = \frac{{0,53}}{{6,{{625.10}^{ - 34}}{{.5.10}^{14}}}}.0,25 = {4.10^{17}}\)(hạt)
Câu hỏi 35 :
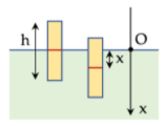
Một vật hình trụ tiết diện nhỏ, có chiều cao \(20\;{\rm{cm}}\), nổi thẳng đứng trong một bể nước rộng. Bỏ qua mọi lực cản, lấy \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\). Khi cân bằng, một nửa vật bị chìm trong nước và mép dưới của vật cách đáy bể một đoạn đủ dài. Từ vị trí cân bằng của vật, truyền cho nó vận tốc ban đầu bằng \(1,5\;{\rm{m}}/{\rm{s}}\) hướng thẳng đứng xuống dưới. Kể từ lúc vật bắt đầu chuyển động đến lúc vận tốc của vật triệt tiêu lần đầu tiên thì tốc độ trung bình của vật gần nhất với giá trị nào sau đây?
- A \(94cm/s.\)
- B \(78cm/s.\)
- C \(85\,cm/s.\)
- D \(98cm/s.\)
Đáp án: C
Phương pháp giải:
- Tìm các lực tác dụng vào vật khi cân bằng.
- Khi tác dụng lực hướng xuống thì coi vật dao động điều hoà → tính lực kéo về → tính \(\omega \) và \(A.\)
- Trong nước vật sẽ chuyển động chậm dần với gia tốc \(a \Rightarrow \)tính \(a.\)
Lời giải chi tiết:
Khi vật cân bằng, tác dụng vào vật có trọng lực và lực đẩy Ác-si-mét:
\(P = {F_A} \Rightarrow V{D_v}g = \frac{V}{2}{D_n}g \Rightarrow {D_n} = 2{D_v}\)
Chọn trục \(Ox\) thẳng đứng hướng xuống:
Khi vật chuyển động thì tác dụng vào vật có
\({F_{kv}} = P - {F_A} \Leftrightarrow {F_{kv}} = mg - \frac{{{D_n}\left( {\frac{h}{2} + x} \right)}}{{{D_v}.h}}mg = \frac{{ - 2mg}}{h}x = - m{\omega ^2}x\)
Tần số góc của dao động là:
\(\omega = \sqrt {\frac{{2g}}{h}} = = \sqrt {\frac{{2.10}}{{0,2}}} = 10\left( {rad/s} \right)\)
Biên độ dao động của vật là: \(A = \frac{{{v_{\max }}}}{\omega } = \frac{{150}}{{10}} = 15\left( {cm} \right)\)
Nhận xét: \(A > \frac{h}{2} \to \) Vật đi xuống 1 đoạn bằng \({S_1} = \frac{h}{2} = 10\,cm\), khi này vật chìm hoàn toàn trong nước và có tốc độ là:
\(v = \omega \sqrt {{A^2} - {x^2}} = 10\sqrt {{{15}^2} - {{10}^2}} = 0,5\sqrt 5 \left( {m/s} \right)\).
Thời gian vật đi hết quãng đường \({S_1}\) là: \({t_1} = \frac{\alpha }{\omega } = \frac{{\arcsin \left( {\frac{{10}}{{15}}} \right)}}{{10}}\)
Theo định luật II Niu – tơn:
\(\begin{array}{l}{F_{kv}} = P - {F_A} \Rightarrow ma = mg - {D_n}.V.g\\ \Rightarrow {D_v}.V.a = {D_v}.V.g - {D_n}.V.g\end{array}\)
Lúc này vật chuyển động chậm dần với gia tốc là
\(a = \left( {1 - \frac{{{D_n}}}{{{D_v}}}} \right)g = - g = - 10\left( {m/{s^2}} \right)\)
Do đó quãng đường và thời gian vật đi tiếp đến khi dừng là:
\(\left\{ \begin{array}{l}S = \frac{{{v^2}}}{{2\left| a \right|}} = \frac{1}{{16}}m = 6,25\left( {cm} \right)\\{t_2} = \frac{v}{{\left| a \right|}} = \frac{1}{{4\sqrt 5 }}\left( s \right)\end{array} \right.\)
Tốc độ trung bình của vật là:
\({v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}} = \frac{{10 + 6,25}}{{\frac{{ar\sin \left( {\frac{{10}}{{15}}} \right)}}{{10}} + \frac{1}{{4\sqrt 5 }}}} \approx 87,94\left( {cm/s} \right)\)
Câu hỏi 36 :
Trong bài thí nghiệm thực hành "Khảo sát thực nghiệm các định luật dao động của con lắc đơn", một nhóm học sinh đo thời gian 10 dao động toàn phần liên tiếp và thu được kết quả \(t = 18,025 \pm 0,247\;s\); đo chiều dài dây treo và thu được kết quả \(l = 0,81 \pm 0,01\;m.\) Cho số \(\pi = 3,140 \pm 0,026\). Gia tốc trọng trường tại nơi làm thí nghiệm mà nhóm học sinh này đo được là
- A \(g = 9,946 \pm 0,463\;m/{s^2}\)
- B \(g = 9,83 \pm 0,55\;m/{s^2}\)
- C \(g = 9,832 \pm 0,554\;m/{s^2}\)
- D \(g = 9,95 \pm 0,46\;m/{s^2}\)
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính trung bình cộng và sai số.
Lời giải chi tiết:
Theo đề bài, bài toán lấy đến 3 chữ số thập phân
Ta có: \(T = 2\pi \sqrt {\frac{l}{g}} \Rightarrow g = 4{\pi ^2}\frac{l}{{{T^2}}}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\bar g = 4{{\bar \pi }^2}\frac{{\bar l}}{{{{\bar T}^2}}} = 9,832\left( {m/{s^2}} \right)}\\
{\frac{{\Delta g}}{{\bar g}} = 2\frac{{\Delta \pi }}{{\bar \pi }} + \frac{{\Delta l}}{{\bar l}} + 2\frac{{\Delta T}}{{\bar T}} = 0,0563 \Rightarrow \Delta g = 0,554\left( {m/{s^2}} \right)}
\end{array}} \right.\)
Câu hỏi 37 :
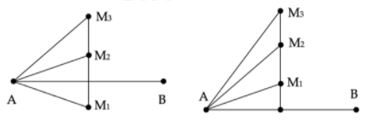
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn đặt tại hai điểm \(A,B\) ở mặt nước dao động điều hòa cùng tần số, cùng pha. Hai điểm cực tiểu liên tiếp trên đoạn \(AB\) cách nhau \(2\;{\rm{cm}}\). Khoảng cách giữa hai nguồn là \(AB = 30\;{\rm{cm}}\). Xét các phần tử nước nằm trên trung trực của \(AB,\,\,{M_1},\,\,{M_2},\,\,{M_3}\) theo thứ tự đó là ba điểm liên tiếp mà phần tử mặt nước ở đó dao động cùng pha với nguồn. Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) gần nhất với giá trị nào sau đây?
- A \(13,5\;{\rm{cm}}\).
- B \(20,5\;{\rm{cm}}\).
- C \(18,5\;{\rm{cm}}\).
- D \(17,5\;{\rm{cm}}\).
Đáp án: C
Phương pháp giải:
- Điểm \(M\) dao động cùng pha với nguồn: \(AM = k\lambda \)
- Đề bài không nói rõ nên ta cần xét 2 trường hợp: \({M_1},\,{M_2}\) cùng phía và \({M_1},\,{M_2}\) khác phía với \(AB.\)
Lời giải chi tiết:
Hai điểm cực tiểu liên tiếp trên đoạn \(AB\) cách nhau \(2\;{\rm{cm}}\)\( \Rightarrow \frac{\lambda }{2} = 2 \Rightarrow \lambda = 4cm.\)
Trên trung trực của \(AB\) có 3 điểm liên liếp \({M_1},\,\,{M_2},\,\,{M_3}\) dao động cùng pha với nguồn và cách nhau xa nhất như hình vẽ.
Để \(M\) cùng pha nguồn thì:
\(AM = k\lambda \ge \frac{{AB}}{2} \Leftrightarrow k.4 \ge 15 \Rightarrow k \ge 3,74 \Rightarrow {k_{\min = 4}}\)
TH1: \({M_1},\,\,{M_2}\) cùng phía với \(AB\) thì lần lượt có \(k = 4,\,5,\,\,6\)
Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) khi này là:
\(\begin{array}{l}{M_1}{M_3} = \sqrt {AM_3^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} - \sqrt {AM_1^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} \\ \Rightarrow {M_1}{M_3} = \sqrt {{{24}^2} - {{15}^2}} - \sqrt {{{16}^2} - {{15}^2}} \approx 13,2\left( {cm} \right)\end{array}\)
TH2: \({M_1},\,\,{M_2}\)khác phía với \(AB\) thì \({M_1}\)và \({M_2}\) đều có \(k = 4\) và \({M_3}\) có \(k = 5.\)
Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) khi này là:
\(\begin{array}{l}{M_1}{M_3} = \sqrt {AM_1^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} + \sqrt {AM_3^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} \\ \Rightarrow {M_1}{M_3} = \sqrt {{{16}^2} - {{15}^2}} + \sqrt {{{24}^2} - {{15}^2}} \approx 18,8\left( {cm} \right)\end{array}\)
Câu hỏi 38 :
Một mạch dao động lí tưởng có độ tự cảm \(L = 4\mu {\rm{H}}\) và điện dung \(C\). Tại thời điểm \(t\) thì cường độ dòng điện tức thời là \(2\;{\rm{mA}}\), tại thời điểm \(t + \frac{{\pi \sqrt {LC} }}{2}\) thì điện áp tức thời trên tụ điện là \(1\;{\rm{V}}\). Giá trị của \(C\) là
- A \(8{\rm{nF}}\).
- B \(32{\rm{pF}}\)
- C \(16{\rm{pF}}\).
- D \(2{\rm{nF}}\).
Đáp án: C
Phương pháp giải:
Tìm mối liên hệ giữa \(t\) và \(T\) từ đó biểu diễn được \(u\) theo \({U_0}\) suy ra \(C.\)
Lời giải chi tiết:
Tại thời điểm \(t:i = 2mA.\)
Tại thời điểm \(t + \frac{{\pi \sqrt {LC} }}{2}:\,\,\,u = 1V\)
Ta có: \(\Delta t = \frac{{\pi \sqrt {LC} }}{2} = \frac{\pi }{{2\omega }} = \frac{{2\pi }}{\omega }.\frac{1}{4} = \frac{T}{4}\)
Mạch chứa L, C thì I và U vuông pha, ta có:
\(\frac{{{i_1}}}{{{I_0}}} = \frac{{{u_2}}}{{{U_0}}} \Leftrightarrow \frac{{0,2}}{{{I_0}}} = \frac{1}{{{I_0}\sqrt {\frac{L}{C}} }} \Rightarrow C = 1,{6.10^{ - 7}}F\)
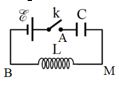
Câu hỏi 39 :
Một mạch dao động \(LC\) lí tưởng được mắc với nguồn điện có suất điện động \(6\;V\), điện trở trong không đáng kể (hình vẽ bên). Điện dung của tụ điện là \(0,5\mu F;\) độ tự cảm của cuộn dây là \(2mH\). Lấy \({\pi ^2} = 10.\) Ban đầu khóa \({\rm{k}}\) ngắt tụ điện chưa tích điện, tại thời điểm \(t = 0\) người ta đóng khóa \({\rm{k}}\) thì trong mạch có dao động điện từ tự do. Kể từ \(t = 0\), thời điểm mà cường độ dòng điện trong mạch có độ lớn \(15\sqrt 3 \pi ({\rm{mA}})\) lần thứ 3 thì điện tích của bản tụ điện nối với khóa \({\rm{k}}\) có giá trị là
- A \( - 1,5\mu C.\)
- B \(1,5\mu C.\)
- C \( - 1,5\sqrt 3 \mu C.\)
- D \(4,5\mu C.\)
Đáp án: B
Phương pháp giải:
Áp dụng định luật bảo toàn năng lượng: \(\frac{1}{2}L{i^2} + \frac{{{q^2}}}{{2C}} = qE\)
Lời giải chi tiết:
Gọi điện tích của bản tụ nối với khoá K là \(q\).
Khi dòng điện đi từ \(M\) đến \(B\) thì \(i > 0\)
Áp dụng định luật bảo toàn năng lượng:
\(\begin{array}{l}\frac{1}{2}L{i^2} + \frac{{{q^2}}}{{2C}} = qE \Rightarrow \frac{1}{2}{2.10^{ - 3}}.{\left( {15\sqrt 3 \pi {{.10}^{ - 3}}} \right)^2} + \frac{{{q^2}}}{{2.0,{{5.10}^{ - 6}}}} = q.6\\ \Rightarrow \left[ \begin{array}{l}{q_1} = 1,5\mu C\\{q_2} = 4,5\mu C\end{array} \right.\end{array}\)
Do \(\left\{ \begin{array}{l}i \bot q\\q \ge 0\end{array} \right.\) (bản tụ nối với cực dương của nguồn) nên lần thứ 3 cường độ dòng điện trong mạch có độ lớn \(15\sqrt 3 \pi ({\rm{mA}}) \Rightarrow q = 4,5\mu C.\)
Câu hỏi 40 :
Sóng dừng trên một sợi dây với hai đầu cố định. Khi tần số sóng là \(f\) thì trên sợi dây có 10 nút sóng (kể cả hai đầu). Nếu tần số sóng là \(\frac{4}{3}f\) thì trên dây có số bụng sóng là
- A 13
- B 12
- C 14
- D 11
Đáp án: B
Phương pháp giải:
Sóng dừng với hai đầu cố định: \(l = k\frac{v}{{2f}}\)
Lời giải chi tiết:
Khi tần số sóng là \(f\) thì \(l = k\dfrac{v}{{2f}} \Rightarrow \dfrac{v}{{2l}} = \dfrac{k}{f} = \dfrac{9}{f}\) (1)
Khi tần số là \(\dfrac{4}{3}f\) thì: \(\dfrac{v}{{2l}} = \dfrac{{3k}}{{4f}}\)(2)
Từ (1) và (2) ta có: \(\dfrac{9}{f} = \dfrac{{3k}}{{4f}} \Rightarrow k = 12\)