Cho hàm số $y = a{x^2}\,\,$ với $a \ne 0$. Kết luận nào sau đây là đúng?
-
A
Hàm số nghịch biến khi $a > 0$ và $x > 0$
-
B
Hàm số nghịch biến khi $a < 0$ và $x < 0$
-
C
Hàm số nghịch biến khi $a > 0$ và $x < 0$
-
D
Hàm số nghịch biến khi $a > 0$ và $x = 0$
Đáp án của giáo viên lời giải hay : C
Cho hàm số $y = {\rm{a}}{{\rm{x}}^2}\,\,(a \ne 0)$.
a) Nếu $a > 0$ thì hàm số nghịch biến khi $x < 0$ và đồng biến khi $x > 0$.
b) Nếu $a < 0$ thì hàm số đồng biến khi $x < 0$ và nghịch biến khi $x > 0$.
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số $y = a{x^2}\,\,$ với $a \ne 0$.
-
A
Đồ thị hàm số nhận trục tung làm trục đối xứng
-
B
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm cao nhất của đồ thị
-
C
Với $a < 0$ đồ thị nằm phía dưới trục hoành và $O$ là điểm cao nhất của đồ thị
-
D
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm thấp nhất của đồ thị
Đáp án của giáo viên lời giải hay : B
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một parabol đi qua gốc tọa độ $O,$ nhận $Oy$ là trục đối xứng ($O$ là đỉnh của parabol).
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, $O$ là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, $O$ là điểm cao nhất của đồ thị.
Giá trị của hàm số $y = f\left( x \right) = - 7{x^2}$ tại ${x_0} = - 2$ là
-
A
$28$
-
B
$14$
-
C
$21$
-
D
$ - 28$
Đáp án của giáo viên lời giải hay : D
Giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) tại điểm \(x = {x_0}\) là \({y_0} = a{x_o}^2\).
Thay ${x_0} = - 2$ vào hàm số $y = f\left( x \right) = - 7{x^2}$ ta được $f\left( { - 2} \right) = - 7.{\left( { - 2} \right)^2} = - 28$
Cho hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}.$
Tìm giá trị của $m$ để đồ thị đi qua điểm $A\left( { - 2;4} \right).$
-
A
$m = 0$
-
B
$m = 1$
-
C
$m = 2$
-
D
$m = - 2$
Đáp án của giáo viên lời giải hay : A
Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_o}^2\).
Thay tọa độ điểm $A\left( { - 2;4} \right)$ vào hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}$ ta được
$\left( { - 2m + 1} \right).{\left( { - 2} \right)^2} = 4 \Leftrightarrow - 2m + 1 = 1 \Leftrightarrow m = 0$
Vậy $m = 0$ là giá trị cần tìm.
Cho hàm số \(y = f\left( x \right) = - 2{x^2}\) . Tổng các giá trị của $a$ thỏa mãn $f\left( a \right) = - 8 + 4\sqrt 3 $ là
-
A
$1$
-
B
$0$
-
C
$10$
-
D
$-10$
Đáp án của giáo viên lời giải hay : B
Giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) tại điểm \(x = {x_0}\) là \({y_0} = a{x_o}^2\).
Ta có $f\left( a \right) = - 8 + 4\sqrt 3 $$ \Leftrightarrow - 2{a^2} = - 8 + 4\sqrt 3 $$ \Leftrightarrow {a^2} = 4 - 2\sqrt 3 $$ \Leftrightarrow {a^2} = {\left( {\sqrt 3 - 1} \right)^2}$
$ \Leftrightarrow \left[ \begin{array}{l}a = \sqrt 3 - 1\\a = 1 - \sqrt 3 \end{array} \right.$
Vậy tổn các giá trị của $a$ là $\left( {\sqrt 3 - 1} \right) + \left( {1 - \sqrt 3 } \right) = 0$
Cho hàm số \(y = \left( {5m + 2} \right){x^2}\) với $m \ne - \dfrac{2}{5}$. Tìm $m$ để hàm số nghịch biến với mọi \(x > 0.\)
-
A
$m < - \dfrac{2}{5}$
-
B
$m > \dfrac{2}{5}$
-
C
$m < \dfrac{2}{5}$
-
D
$m > - \dfrac{5}{2}$
Đáp án của giáo viên lời giải hay : A
Xét hàm số \(y = a{x^2}\left( {a \ne 0} \right).\) Ta có:
+) Nếu \(a > 0\) thì hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0\).
+) Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\).
Để hàm số nghịch biến với mọi \(x > 0\) thì $a < 0$ nên $5m + 2 < 0 \Leftrightarrow m < - \dfrac{2}{5}$.
Vậy $m < - \dfrac{2}{5}$ thỏa mãn điều kiện đề bài.
Cho hàm số \(y = \left( {4 - 3m} \right){x^2}\) với $m \ne \dfrac{4}{3}$. Tìm $m$ để hàm số đồng biến với mọi \(x > 0\)
-
A
$m > \dfrac{4}{3}$
-
B
$m < - \dfrac{4}{3}$
-
C
$m < \dfrac{4}{3}$
-
D
$m < - \dfrac{4}{3}$
Đáp án của giáo viên lời giải hay : C
Xét hàm số \(y = a{x^2}\left( {a \ne 0} \right).\) Ta có:
+) Nếu \(a > 0\) thì hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0\).
+) Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\).
Để hàm số đồng biến với mọi \(x > 0\) thì $a > 0$ nên $4 - 3m > 0 \Leftrightarrow 4>3m$$ \Leftrightarrow 3m<4\Leftrightarrow m < \dfrac{4}{3}$.
Vậy $m < \dfrac{4}{3}$ thỏa mãn điều kiện đề bài
Trong các điểm $A(1;2);B( - 1; - 1);C(10; - 200);D\left( {\sqrt {10} ; - 10} \right)$ có bao nhiêu điểm thuộc đồ thị hàm số $\left( P \right): y = - {x^2}$
-
A
$1$
-
B
$4$
-
C
$3$
-
D
$2$
Đáp án của giáo viên lời giải hay : D
Điểm $M\left( {{x_0};{y_0}} \right)$ thuộc đồ thị hàm số $y = a{x^2}\,\left( {a \ne 0} \right)$ khi ${y_0} = ax_0^2\,$
+) Thay tọa độ điểm $A\left( {1;2} \right)$ vào hàm số $y = - {x^2}$ ta được $2 = - {1^2}$( vô lý) nên $A \notin \left( P \right)$
+) Thay tọa độ điểm $C\left( {10; - 200} \right)$ vào hàm số $y = - {x^2}$ ta được $ - 200 = - {\left( {10} \right)^2} \Leftrightarrow - 200 = - 100$( vô lý) nên loại $C \notin \left( P \right)$
+) Thay tọa độ điểm $D\left( {\sqrt {10} ; - 10} \right)$ vào hàm số $y = - {x^2}$ ta được $ - 10 = - {\left( {\sqrt {10} } \right)^2} \Leftrightarrow - 10 = - 10$( luôn đúng) nên $D \in \left( P \right)$
+) Thay tọa độ điểm $B\left( { - 1; - 1} \right)$ vào hàm số $y = - {x^2}$ ta được $ - 1 = - {\left( { - 1} \right)^2} \Leftrightarrow - 1 = - 1$ (luôn đúng)
$B \in \left( P \right)$.
Cho hàm số \(y = f\left( x \right) = 3{x^2}\). Tìm $b$ biết \(f\left( b \right) \ge 6b + 9\).
-
A
$1 < b < 3$
-
B
$ - 1 \le b \le 3$
-
C
$\left[ \begin{array}{l}b \le - 1\\b \ge 3\end{array} \right.$
-
D
$\left[ \begin{array}{l}b < - 1\\b > 3\end{array} \right.$
Đáp án của giáo viên lời giải hay : C
Sử dụng : Giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) tại điểm \(x = {x_0}\) là \({y_0} = a{x_o}^2\)
Sau đó giải bất bất phương trình thu được
Ta có \(f\left( b \right) \ge 6b + 9\) $ \Leftrightarrow 3{b^2} \ge 6b + 9 \Leftrightarrow {b^2} - 2b - 3 \ge 0$$ \Leftrightarrow \left( {b + 1} \right)\left( {b - 3} \right) \ge 0 $
\(\begin{array}{l}
TH1:\left\{ \begin{array}{l}
b + 1 \ge 0\\
b - 3 \ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b \ge - 1\\
b \ge 3
\end{array} \right. \Rightarrow b \ge 3\\
TH2:\left\{ \begin{array}{l}
b + 1 \le 0\\
b - 3 \le 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b \le - 1\\
b \le 3
\end{array} \right. \Rightarrow b \le - 1
\end{array}\)
Vậy $\left[ \begin{array}{l}b \le - 1\\b \ge 3\end{array} \right.$ là giá trị cần tìm.
Cho hàm số \(y = \left( {2m + 2} \right){x^2}\). Tìm $m$ để đồ thị hàm số đi qua điểm $A\left( {x;y} \right)$ với $\left( {x;y} \right)$ là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\)
-
A
$m = \dfrac{7}{4}$
-
B
$m = \dfrac{1}{4}$
-
C
$m = \dfrac{7}{8}$
-
D
$m = - \dfrac{7}{8}$
Đáp án của giáo viên lời giải hay : D
Bước 1: Giải hệ phương trình cho trước bằng phương pháp thế hoặc cộng đại số ta tìm được $\left( {x;y} \right)$
Bước 2: Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_o}^2\) từ đó tìm được $m$
Ta có \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}x = y + 1\\2\left( {y + 1} \right) - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.$$ \Rightarrow A\left( {2;1} \right)$
Thay $x = 2;y = 1$ vào hàm số \(y = \left( {2m + 2} \right){x^2}\) ta được
$1 = \left( {2m + 2} \right){.2^2} \Leftrightarrow 2m + 2 = \dfrac{1}{4} \Leftrightarrow 2m = \dfrac{{ - 7}}{4} \Leftrightarrow m = \dfrac{{ - 7}}{8}$
Vậy $m = - \dfrac{7}{8}$ là giá trị cần tìm.
Cho hàm số \(y = \left( { - {m^2} + 4m - 5} \right){x^2}\) . Kết luận nào sau đây là đúng
-
A
Đồ thị của hàm số nằm phía trên trục hoành
-
B
Đồ thị của hàm số nhận gốc tọa độ $O$ là điểm cao nhất
-
C
Hàm số nghịch biến với $x < 0$
-
D
Hàm số đồng biến với $x > 0$
Đáp án của giáo viên lời giải hay : B
Bước 1: Đánh giá hệ số $a$ của ${x^2}$
Bước 2: Ta sử dụng các kiến thức sau để kết luận
* Xét hàm số \(y = a{x^2}\left( {a \ne 0} \right).\) Ta có:
- Nếu \(a > 0\) thì hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0\).
- Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\).
* Đồ thị của hàm số $y = a{x^2}\,\,\left( {a \ne 0} \right)$ là một đường cong (parabol) đi qua gốc tọa độ $O$.
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Ta thấy hàm số \(y = \left( { - {m^2} + 4m - 5} \right){x^2}\) có
$a = - {m^2} + 4m - 5 = - \left( {{m^2} - 4m + 4} \right) - 1 = - {\left( {m - 2} \right)^2} - 1$
Vì \((m-2)^2\ge 0\) với mọi \(m\) nên \(-(m-2)^2\le 0\) với mọi m
Suy ra \(-(m-2)^2-1\le 0-1\Rightarrow -(m-2)^2-1\le -1<0\) với mọi m
Hay \(a<0\) với mọi m
Nên hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\). Suy ra C,D sai.
Và đồ thị hàm số nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Suy ra A sai.
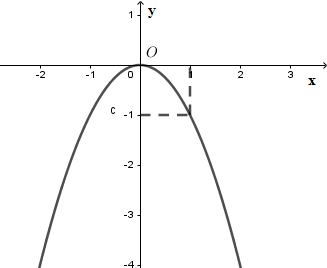
Hình vẽ dưới đây là của đồ thị hàm số nào?
-
A
$y = - {x^2}$
-
B
$y = {x^2}$
-
C
$y = 2{x^2}$
-
D
$y = - 2{x^2}$
Đáp án của giáo viên lời giải hay : A
Ta sử dụng các kiến thức sau:
* Đồ thị của hàm số $y = a{x^2}\,\,\left( {a \ne 0} \right)$ là một đường cong (parabol) đi qua gốc tọa độ $O$.
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
* Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_o}^2\)
Từ hình vẽ suy ra $a < 0$ nên loại B,C
Vì đồ thị đi qua điểm có tọa độ $\left( {1; - 1} \right)$ nên loại D.
Cho hàm số $y = \sqrt 3 {x^2}\,\,$có đồ thị là $(P)$. Có bao nhiêu điểm trên $\left( P \right)$ có tung độ gấp đôi hoành độ.
-
A
$5$
-
B
$4$
-
C
$3$
-
D
$2$
Đáp án của giáo viên lời giải hay : D
Bước 1: Gọi điểm $M$$\left( {x;y} \right)$ thỏa mãn điều kiện đề bài. Biểu diễn $x$ theo $y$ hoặc $y$ theo$x$ .
Bước 2: Thay tọa độ điểm $M$ vào hàm số ta tìm được $x$ từ đó suy ra $M$ .
Gọi điểm $M$$\left( {x;y} \right)$ là điểm cần tìm. Vì $M$ có tung độ gấp đôi hoành độ nên $M\left( {x;2x} \right)$.
Thay tọa độ điểm $M$ vào hàm số ta được
$2x = \sqrt 3 {x^2} \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 0\\x = \dfrac{{2\sqrt 3 }}{3} \Rightarrow y = \dfrac{{4\sqrt 3 }}{3}\end{array} \right.$
Hay có hai điểm thỏa mãn điều kiện là $O\left( {0;0} \right),M\left( {\dfrac{{2\sqrt 3 }}{3};\dfrac{{4\sqrt 3 }}{3}} \right)$.
Cho $(P):y = \dfrac{1}{2}{x^2};(d):y = x - \dfrac{1}{2}$. Tìm toạ độ giao điểm của $(P)$ và $(d)$.
-
A
$\left( {1;\dfrac{1}{2}} \right)$
-
B
$\left( {1;2} \right)$
-
C
$\left( {\dfrac{1}{2};1} \right)$
-
D
$\left( {2;1} \right)$
Đáp án của giáo viên lời giải hay : A
Cho parabol $(P):y = {\rm{a}}{{\rm{x}}^2}(a \ne 0)$ và đường thẳng $d:y = mx + n$. Để tìm tọa độ giao điểm (nếu có) của $(d)$ và $(P)$, ta làm như sau:
Bước 1. Xét phương trình hoành độ giao điểm của $(d)$ và $(P)$ :${\rm{a}}{{\rm{x}}^2} = mx + n$
Bước 2. Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó ta tìm được tọa độ giao điểm của $(d)$ và $(P)$
Xét phương trình hoành độ giao điểm của parabol $\left( P \right)$ và đường thẳng $d$
$\dfrac{1}{2}{x^2} = x - \dfrac{1}{2} \Leftrightarrow {x^2} - 2x + 1 = 0 \Leftrightarrow {\left( {x - 1} \right)^2} = 0 $$\Leftrightarrow x-1=0\Leftrightarrow x = 1$
Thay \(x=1\) vào hàm số \(y=\dfrac{1}{2}x^2\) ta được \( y = \dfrac{1}{2}.1^2=\dfrac{1}{2}\)
Nên tọa độ giao điểm cần tìm là $\left( {1;\dfrac{1}{2}} \right)$.
Cho parabol \(y = \dfrac{1}{4}{x^2}\). Xác định \(m\) để điểm \(A\left( {\sqrt 2 ;m} \right)\) nằm trên parabol.
-
A
\(m = \dfrac{1}{2}\)
-
B
\(m = - \dfrac{1}{2}\)
-
C
\(m = 2\)
-
D
\(m = - 2\)
Đáp án của giáo viên lời giải hay : A
Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_o}^2\) từ đó tìm được \(m\)
Thay \(x = \sqrt 2 ;y = m\) vào hàm số \(y = \dfrac{1}{4}{x^2}\) ta được \(m = \dfrac{1}{4}.{\left( {\sqrt 2 } \right)^2} = \dfrac{1}{2}.\)
Vậy \(m = \dfrac{1}{2}.\)
Cho parabol$(P):y = 2{x^2}$ và đường thẳng $(d):y = x + 1$. Số giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là:
-
A
$1$
-
B
$0$
-
C
$3$
-
D
$2$
Đáp án của giáo viên lời giải hay : D
Cho parabol $(P):y = {\rm{a}}{{\rm{x}}^2}(a \ne 0)$ và đường thẳng $d:y = mx + n$. Để tìm tọa độ giao điểm (nếu có) của $(d)$ và $(P)$, ta làm như sau:
Bước 1. Xét phương trình hoành độ giao điểm của $(d)$ và $(P)$ :$ax^2 = mx + n$
Bước 2. Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó suy ra số giao điểm của parabol và đường thẳng.
Xét phương trình hoành độ giao điểm của parabol $\left( P \right)$ và đường thẳng $d$
$2{x^2} = x + 1 \Leftrightarrow 2{x^2} - x - 1 = 0 \\\Leftrightarrow 2{x^2} - 2x + x - 1 = 0 \\\Leftrightarrow 2x\left( {x - 1} \right) + \left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {2x + 1} \right)\left( {x - 1} \right) = 0$
$ \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\x = 1\end{array} \right.$
Vậy có hai giao điểm của đường thẳng $d$ và parabol $\left( P \right)$.
Cho parabol $(P):y = \left( {m - 1} \right){x^2}$ và đường thẳng $(d):y = 3 - 2x$. Tìm $m$ để đường thẳng $d$ cắt $\left( P \right)$ tại điểm có tung độ $y = 5$.
-
A
$m = 5$
-
B
$m = 7$
-
C
$m = 6$
-
D
$m =-6$
Đáp án của giáo viên lời giải hay : C
Bước 1: Thay tung độ giao điểm vào phương trình đường thẳng $d$ để tìm hoành độ giao điểm.
Bước 2: Thay tọa độ giao điểm vào phương trình parabol ta tìm được $m$.
Thay $y = 5$ vào phương trình đường thẳng $d$ ta được $5 = 3 - 2x \Leftrightarrow x = - 1$
Nên tọa độ giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là $\left( { - 1;5} \right)$
Thay $x = - 1;y = 5$ vào hàm số $y = \left( {m - 1} \right){x^2}$ ta được
$\left( {m - 1} \right).{\left( { - 1} \right)^2} = 5 \Leftrightarrow m - 1 = 5 \Leftrightarrow m = 6$
Vậy $m = 6$ là giá trị cần tìm.
Cho parabol $(P):y = \left( {\dfrac{{1 - 2m}}{2}} \right){x^2}$ và đường thẳng $(d):y = 2x + 2$. Biết đường thẳng $d$ cắt $\left( P \right)$ tại một điểm có tung độ $y = 4$. Tìm hoành độ giao điểm còn lại của $d$ và parabol $\left( P \right)$.
-
A
$x = - \dfrac{1}{2}$
-
B
$x = \dfrac{1}{2}$
-
C
$x = - \dfrac{1}{4}$
-
D
$x = \dfrac{1}{4}$
Đáp án của giáo viên lời giải hay : A
Bước 1: Thay tung độ giao điểm vào phương trình đường thẳng $d$ để tìm hoành độ giao điểm.
Bước 2: Thay tọa độ giao điểm vào phương trình parabol ta tìm được $m$.
Bước 3: Giải phương trình hoành độ giao điểm của $d$ và parabol $\left( P \right)$ ta tìm được hoành độ giao điểm còn lại.
Thay $y = 4$ vào phương trình đường thẳng $d$ ta được $2x + 2 = 4 \Leftrightarrow x = 1$
Nên tọa độ giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là $\left( {1;4} \right)$
Thay $x = 1;y = 4$ vào hàm số $y = \left( {\dfrac{{1 - 2m}}{2}} \right){x^2}$ ta được
$\dfrac{{1 - 2m}}{2}{.1^2} = 4 \Leftrightarrow 1 - 2m = 8 \Leftrightarrow m = - \dfrac{7}{2}$$ \Rightarrow \left( P \right):y = 4{x^2}$
Xét phương trình hoành độ giao điểm của $d$ và $\left( P \right)$ :
$4{x^2} = 2x + 2 \Leftrightarrow 2{x^2} - x - 1 = 0 \Leftrightarrow \left( {2x + 1} \right)\left( {x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \dfrac{1}{2}\end{array} \right.$
Vậy hoành độ giao điểm còn lại là $x = - \dfrac{1}{2}$.
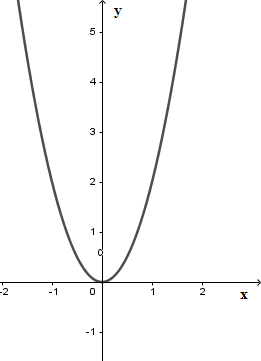
Cho đồ thị hàm số $y = 2{x^2}$$\left( P \right)$ như hình vẽ. Dựa vào đồ thị, tìm $m$ để phương trình $2{x^2} - m - 5 = 0$ có hai nghiệm phân biệt.
-
A
$m < - 5$
-
B
$m > 0$
-
C
$m < 0$
-
D
$m > - 5$
Đáp án của giáo viên lời giải hay : D
Đưa phương trình về dạng ${\rm{a}}{{\rm{x}}^2} = mx + n$ (*)
Gọi parabol $\left( P \right):y = a{x^2}$ và đường thẳng $d:y = mx + n$
Số nghiệm của (*) bằng đúng số giao điểm của .
- Nếu $(d)$ không cắt $(P)$ thì (*) vô nghiệm
- Nếu $(d)$ tiếp xúc với $(P)$ thì (*) có nghiệm kép
- Nếu $(d)$ cắt $(P)$ tại hai điểm phân biệt thì (*) có 2 nghiệm phân biệt .
Ta có $2{x^2} - m - 5 = 0$ (*) $ \Leftrightarrow 2{x^2} = m + 5$
Số nghiệm của phương trình (*) là số giao điểm của parabol $\left( P \right):y = 2{x^2}$ và đường thẳng $d:y = m + 5$.
Để (*) có hai nghiệm phân biệt thì $d$ cắt $\left( P \right)$ tại hai điểm phân biệt. Từ đồ thị hàm số ta thấy
Với $m + 5 > 0 \Leftrightarrow m > - 5$ thì $d$ cắt $\left( P \right)$ tại hai điểm phân biệt hay phương trình (*) có hai nghiệm phân biệt khi $m > - 5$.
Lực \(F\) của gió thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương vận tốc \(v\) của gióm tức là: \(F = a{v^2}\) với \(a\) là hằng số. Biết rằng khi vận tốc của gió là \(2,5m/s\) thì lực tác động lên cánh buồm là \(150N.\) Biết thuyền buồm vẫn có thể đi được nếu vận tốc gió lớn nhất là \(90km/h.\) Tính áp lực lớn nhất mà cánh buồm có thể chịu được.
-
A
\(15000N\)
-
B
\(12000N\)
-
C
\(13500N\)
-
D
\(14000N\)
Đáp án của giáo viên lời giải hay : A
Tính hằng số \(a.\)
Khi đó ta có biểu thức \(F = a{v^2}\) và có vận tốc gió lớn nhất mà thuyền buồm có thể chịu được thì \({F_{\max }} = a.v_{\max }^2.\)
Chú ý đổi đơn vị vận tốc của gió.
Theo đề bài ta có: vận tốc của gió là \(2,5m/s\) thì lực tác động lên cánh buồm là \(150N\)
\( \Rightarrow 150 = a.2,{5^2} \Leftrightarrow a = 24\,\,\left( {N{s^2}/{m^2}} \right).\)
Khi đó ta có: \(F = 24{v^2}.\)
Đổi: \({v_{\max }} = 90km/h = \dfrac{{90.1000}}{{3600}} = 25\,\,m/s.\)
Như vậy áp lực lớn nhất mà thuyền buồm có thể chịu được là:
\({F_{\max }} = 24v_{\max }^2 = {24.25^2} = 15000\,\,N.\)
Giá trị nhỏ nhất của hàm số \(y = - 2{x^2}\) khi \(x \in \left[ { - 3;\,\,5} \right]\) là:
-
A
\(\mathop {Min}\limits_{\left[ { - 3;\,\,5} \right]} y = 18\)
-
B
\(\mathop {Min}\limits_{\left[ { - 3;\,\,5} \right]} y = - 50\)
-
C
\(\mathop {Min}\limits_{\left[ { - 3;\,\,5} \right]} y = - 18\)
-
D
\(\mathop {Min}\limits_{\left[ { - 3;\,\,5} \right]} y = 50\)
Đáp án của giáo viên lời giải hay : B
Xét hàm số: \(y = a{x^2}\,\,\,\left( {a \ne 0} \right)\) ta có:
+) TH1: \(a > 0\) thì hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0.\)
+) TH2: \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0.\)
Ta có: \(y = - 2{x^2}\) có \(a = - 2 < 0 \Rightarrow \) đồ thị hàm số có bề lõm hướng xuống dưới.
Và hàm số đồng biến khi \(x > 0,\) hàm số nghịch biến khi \(x < 0.\)
+) Với \( - 3 \le x < 0\) ta có: \(y\left( { - 3} \right) \le y\left( x \right) < y\left( 0 \right) \Leftrightarrow - 18 \le y\left( x \right) < 0.\)
+) Với \(0 \le x \le 5\) ta có: \(y\left( 0 \right) \ge y\left( x \right) \ge y\left( 5 \right) \Leftrightarrow 0 \ge y\left( x \right) \ge - 50\)
\( \Rightarrow \) Với mọi \(x \in \left[ { - 3;\,\,5} \right]\) ta có: \( - 50 \le y\left( x \right) \le 0\)
Vậy \(\mathop {Min}\limits_{\left[ { - 3;\,\,5} \right]} y = y\left( { - 5} \right) = - 50.\)
Tìm tất cả các giá trị của tham số \(m\) để đường thẳng \(y = x + 3 - m\) cắt parabol \(y = {x^2}\) tại hai điểm phân biệt.
-
A
\(m < \dfrac{{13}}{4}\)
-
B
\(m < 3\)
-
C
\(m > 3\)
-
D
\(m > \dfrac{13}{4}\)
Đáp án của giáo viên lời giải hay : A
Xét phương trình hoành độ giao điểm (*) của hai đồ thị hàm số.
Đường thẳng \(d\) cắt parabol \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \) Phương trình \(\left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\)
Xét phương trình hoành độ giao điểm của đường thẳng \(d:\,\,\,y = x + 3 - m\) và parabol \(\left( P \right):\,\,y = {x^2}\) ta có:
\({x^2} = x + 3 - m\) \( \Leftrightarrow {x^2} - x + m - 3 = 0\,\,\,\,\left( * \right)\)
Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta > 0 \Leftrightarrow 1 - 4\left( {m - 3} \right) > 0\\ \Leftrightarrow 1 - 4m + 12 > 0\\ \Leftrightarrow 4m < 13 \Leftrightarrow m < \dfrac{{13}}{4}.\end{array}\)
Vậy \(m < \dfrac{{13}}{4}\) thỏa mãn bài toán.
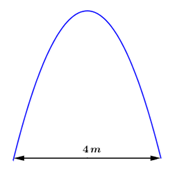
Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số \(y = - {x^2}.\) Biết khoảng cách giữa hai chân cổng là \(4\,m.\) Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là \(2,4\,m.\) Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng?
-
A
\(2,\,4\,m\)
-
B
\(1,44\,m\)
-
C
\(4\,m\)
-
D
\(2,56\,m\)
Đáp án của giáo viên lời giải hay : B
Sử dụng phương pháp tọa độ hóa tức gắn vào hệ trục tọa độ để tính toán.
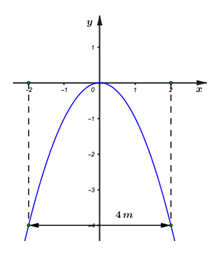
Ta có đồ thị hàm số của cổng biệt thự như hình vẽ.
Khi đó cổng biệt thự có chiều cao \(h = 4\,m.\)
Chiều rộng của thùng xe ô tô tải là \(2,4\,m \Rightarrow {x_0} = \dfrac{1}{2}.2,4 = 1,2m.\)
\( \Rightarrow \) Chiều cao lớn nhất của ô tô tải là: \({h_0} = 1,{2^2} = 1,44m.\)
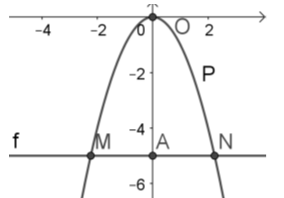
Cho parabol \(y=-{{x}^{2}}\). Vẽ đường thẳng song song với trục hoành cắt trục tung tại điểm \(-5\) và cắt parabol tại \(M\) và \(N\). Diện tích tam giác \(OMN\) là
-
A
\(10\)
-
B
\(5\sqrt{5}\)
-
C
\(\dfrac{25}{2}\)
-
D
\(5\sqrt{2}\)
Đáp án của giáo viên lời giải hay : B
Hoành độ giao điểm hai đồ thị \(y={{f}_{1}}\left( x \right)\) và \(y={{f}_{2}}\left( x \right)\) là nghiệm của phương trình \({{f}_{1}}\left( x \right)-{{f}_{2}}\left( x \right)=0\)
Công thức tính diện tích tam giác: \(S=\frac{1}{2}a.h\) (\(a\) là độ dài đáy, \(h\) là chiều cao tương ứng)
Đường thẳng song song với \(Ox\) cắt \(Oy\) tại \(-5\) là đường thẳng \(f:y=-5\). Hoành độ giao điểm của \(\left( P \right)\) và \(f\) là nghiệm của phương trình \(-{{x}^{2}}=-5\Rightarrow \left[ \begin{align}& x=\sqrt{5} \\& x=-\sqrt{5} \\\end{align} \right.\). Vậy \(M(-\sqrt{5};-5);N(\sqrt{5};-5)\).
Ta có : \(MN=AM+AN=\left| -\sqrt{5} \right|+\left| \sqrt{5} \right|=2\sqrt{5}\)
\(OA=\left| -5 \right|=5\)
Vậy \({{S}_{OMN}}=\dfrac{1}{2}MN.OA=\dfrac{1}{2}.2\sqrt{5}.5=5\sqrt{5}\).
Cho parabol \(\left( P \right):y=f\left( x \right)={{x}^{2}}\) . Đường thẳng \(d:y=m\) cắt \(\left( P \right)\) tại hai điểm \(A\) và \(B\) sao cho tam giác \(OAB\) đều.
-
A
\(m=0\)
-
B
\(m=3\)
-
C
Cả A và B đúng
-
D
Cả A và B đều sai
Đáp án của giáo viên lời giải hay : B
Hoành độ giao điểm hai đồ thị \(y={{f}_{1}}\left( x \right)\) và \(y={{f}_{2}}\left( x \right)\) là nghiệm của phương trình \({{f}_{1}}\left( x \right)-\text{ }{{f}_{2}}\left( x \right)=0\)
Hai đồ thị hàm số cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình hoành độ giao điểm có \(2\) nghiệm phân biệt.
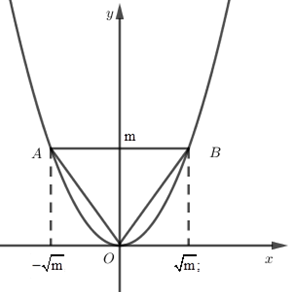
\(\left( P \right)\) cắt \(d\) tại \(2\) điểm phân biệt \(\Leftrightarrow \) phương trình hoành độ giao điểm \({{x}^{2}}-m=0\) phải có hai nghiệm phân biệt suy ra \(m>0\).
Ta có hoành độ của \(A\) và \(B\) là nghiệm của phương trình \({{x}^{2}}=m\Leftrightarrow \left[ \begin{align}& x=\sqrt{m} \\ & x=-\sqrt{m} \\\end{align} \right.\).
Vậy \(A\left( -\sqrt{m};m \right),B\left( \sqrt{m},m \right)\).
Để \(OAB\) là tam giác đều thì \(OA=OB=AB\)
Mà \(OA=\sqrt{{{\left( -\sqrt{m} \right)}^{2}}+{{m}^{2}}},OB=\sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}\)
\(AB=\left| -\sqrt{m} \right|+\left| \sqrt{m} \right|=2\sqrt{m}\)
Nên ta có \(\sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}=2\sqrt{m}\Leftrightarrow m+{{m}^{2}}=4m\)
\(\Leftrightarrow {{m}^{2}}-3m=0\Leftrightarrow \left[ \begin{align} & m=0 \\ & m=3 \\\end{align} \right.\)
Kết hợp điều kiện \(m>0\) ta được \(m=3\).
