Đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$$\left( {a \ne 0} \right)$ tiếp xúc với nhau khi phương trình $a{x^2} = mx + n$ có
-
A
Hai nghiệm phân biệt
-
B
Nghiệm kép
-
C
Vô nghiệm
-
D
Có hai nghiệm âm.
Đáp án của giáo viên lời giải hay : B
Đường thẳng $d$ và parabol $\left( P \right)$ tiếp xúc với nhau khi phương trình
$a{x^2} = mx + n \Leftrightarrow a{x^2} - mx - n = 0$ có nghiệm kép $\left( {\Delta = 0} \right)$
Chọn khẳng định đúng. Nếu phương trình $a{x^2} = mx + n$ vô nghiệm thì đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$
-
A
Cắt nhau tại hai điểm
-
B
Tiếp xúc với nhau
-
C
Không cắt nhau
-
D
Cắt nhau tại gốc tọa độ
Đáp án của giáo viên lời giải hay : C
Đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$ không cắt nhau khi phương trình $a{x^2} = mx + n$ vô nghiệm.
Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
-
A
$2$
-
B
$1$
-
C
$0$
-
D
$3$
Đáp án của giáo viên lời giải hay : A
Bước 1: Giải phương trình hoành độ giao điểm.
Bước 2: Số nghiệm vừa tìm được của phương trình là số giao điểm của đường thẳng và parabol
Xét phương trình hoành độ giao điểm ${x^2} = 2x + 4 \Leftrightarrow {x^2} - 2x - 4 = 0$ có $\Delta ' = 5 > 0$ nên phương trình có hai nghiệm phân biệt hay đường thẳng cắt parabol tại hai điểm phân biệt.
Tìm tham số $m$ để đường thẳng $d:y = \dfrac{1}{2}x + m$ tiếp xúc với parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$
-
A
$m = \dfrac{1}{4}$
-
B
$m = - \dfrac{1}{4}$
-
C
$m = \dfrac{1}{8}$
-
D
$m = - \dfrac{1}{8}$
Đáp án của giáo viên lời giải hay : D
Bước 1: Xét phương trình hoành độ giao điểm của đường thẳng và parabol
Bước 2: Để đường thẳng tiếp xúc với parabol thì phương trình hoành độ giao điểm có nghiệm kép
Xét phương trình hoành độ giao điểm $\dfrac{{{x^2}}}{2} = \dfrac{1}{2}x + m \Leftrightarrow {x^2} - x - 2m = 0$ có $\Delta = 8m + 1$
Để đường thẳng $d$ tiếp xúc với parabol $\left( P \right)$ thì $\Delta = 0 \Leftrightarrow 8m + 1 = 0 \Leftrightarrow m = - \dfrac{1}{8}$.
Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt
-
A
$m = 2$
-
B
$m = - 2$
-
C
$m = 4$
-
D
$m \in \mathbb{R}$
Đáp án của giáo viên lời giải hay : D
Bước 1: Xét phương trình hoành độ giao điểm của đường thẳng và parabol
Bước 2: Để đường thẳng cắt parabol tại hai điểm phân biệt thì phương trình hoành độ giao điểm có hai nghiệm phân biệt.
Xét phương trình hoành độ giao điểm $\dfrac{{{x^2}}}{2} = mx + 2 \Leftrightarrow {x^2} - 2mx - 4 = 0$ có $\Delta ' = {m^2} + 4$
Vì $\Delta ' = {m^2} + 4 > 0;\forall m$ nên đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt với mọi $m$.
Tìm tham số $m$ để đường thẳng $d:y = 2x + m$ và parabol $\left( P \right):y = 2{x^2}$ không có điểm chung
-
A
$m < - \dfrac{1}{2}$
-
B
$m \le - \dfrac{1}{2}$
-
C
$m > \dfrac{1}{2}$
-
D
$m \ge \dfrac{1}{2}$
Đáp án của giáo viên lời giải hay : A
Bước 1: Xét phương trình hoành độ giao điểm của đường thẳng và parabol
Bước 2: Để đường thẳng không cắt parabol thì phương trình hoành độ giao điểm vô nghiệm
Xét phương trình hoành độ giao điểm $2{x^2} = 2x + m \Leftrightarrow 2{x^2} - 2x - m = 0$ có $\Delta ' = 1 + 2m$
Để đường thẳng $d:y = 2x + m$ không cắt parabol $\left( P \right):y = 2{x^2}$ thì $\Delta ' < 0 \Leftrightarrow 2m + 1 < 0 \Leftrightarrow m < - \dfrac{1}{2}$
Tìm tham số $m$ để đường thẳng $d:y = mx + m + 1$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt nằm bên trái trục tung.
-
A
$\left\{ \begin{array}{l}m < 0\\m \ne - 2\end{array} \right.$
-
B
$\left\{ \begin{array}{l}m < - 1\\m \ne - 2\end{array} \right.$
-
C
$m > - 1$
-
D
$m \ge - 2$
Đáp án của giáo viên lời giải hay : B
Bước 1: Viết phương trình hoành độ giao điểm (*)
Bước 2: Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm bên trái trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm âm phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S < 0\\P > 0\end{array} \right.$
Phương trình hoành độ giao điểm ${x^2} = mx + m + 1 \Leftrightarrow {x^2} - mx - m - 1 = 0\left( * \right)$ có
$\Delta = {m^2} - 4\left( { - m - 1} \right) = {m^2} + 4m + 4 = {\left( {m + 2} \right)^2} \ge 0$, $\forall m$; $S = {x_1} + {x_2} = m;P = {x_1}.{x_2} = - m - 1$ với ${x_1};{x_2}$ là hai nghiệm của phương trình (*).
Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm bên trái trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm âm phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S < 0\\P > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 2} \right)^2} > 0\\m < 0\\ - m - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 2\\m < 0\\m < - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < - 1\\m \ne - 2\end{array} \right.$
Vậy $\left\{ \begin{array}{l}m < - 1\\m \ne - 2\end{array} \right.$ .
Tìm tham số $m$ để đường thẳng $d:y = \left( {m - 2} \right)x + 3m$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt nằm hai phía của trục tung.
-
A
$m < 3$
-
B
$m > 3$
-
C
$m > 2$
-
D
$m > 0$
Đáp án của giáo viên lời giải hay : D
Bước 1: Viết phương trình hoành độ giao điểm (*)
Bước 2: Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm hai phía trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm trái dấu$ \Leftrightarrow ac < 0$
Phương trình hoành độ giao điểm ${x^2} = \left( {m - 2} \right)x + 3m $
$\Leftrightarrow {x^2} - \left( {m - 2} \right)x - 3m = 0$
Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm hai phía trục tung
$ \Leftrightarrow $ phương trình (*) có hai nghiệm trái dấu
$ \Leftrightarrow ac < 0$
$ \Leftrightarrow - 3m < 0 \Leftrightarrow m > 0$.
Có bao nhiêu giá trị của tham số $m$ để đường thẳng $d:y = 2mx + 4$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn $\dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}} = - 3$
-
A
$1$
-
B
$2$
-
C
$3$
-
D
$0$
Đáp án của giáo viên lời giải hay : B
Bước 1: Viết phương trình hoành độ giao điểm (*)
Bước 2: Tìm điều kiện để đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt
Bước 3: Biến đổi biểu thức đã cho để sử dụng hệ thức Vi-et và tìm $m$.
Phương trình hoành độ giao điểm ${x^2} = 2mx + 4 \Leftrightarrow {x^2} - 2mx - 4 = 0$ có $\Delta ' = {m^2} + 4 > 0;\forall m$
nên đường thẳng $d$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$
Theo hệ thức Vi-et ta có $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = - 4\end{array} \right.$(${x_1};{x_2} \ne 0$)
Ta có $\dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}} = - 3$$ \Leftrightarrow \dfrac{{{x_1}^2 + x_2^2}}{{{x_1}{x_2}}} = - 3 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} + {x_1}{x_2} = 0 \Leftrightarrow 4{m^2} - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.$
Vậy $m = 1;m = - 1$ là các giá trị cần tìm.
Có bao nhiêu giá trị nguyên của tham số $m$ để đường thẳng $d:y = 2mx - 2m + 3$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt có tọa độ $\left( {{x_1};{y_1}} \right);\left( {{x_2};{y_2}} \right)$ thỏa mãn ${y_1} + {y_2} < 9$
-
A
$1$
-
B
$3$
-
C
$2$
-
D
$0$
Đáp án của giáo viên lời giải hay : C
Bước 1: Viết phương trình hoành độ giao điểm (*)
Bước 2: Tìm điều kiện để đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt
Bước 3: Biến đổi biểu thức đã cho để sử dụng hệ thức Vi-et và tìm $m$.
Phương trình hoành độ giao điểm ${x^2} = 2mx - 2m + 3 \Leftrightarrow {x^2} - 2mx + 2m - 3 = 0$ có $\Delta ' = {m^2} - 2m + 3 = {\left( {m - 1} \right)^2} + 2 > 0;\forall m$
Nên nên đường thẳng $d$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt có tọa độ $\left( {{x_1};{y_1}} \right);\left( {{x_2};{y_2}} \right)$
Ta có ${y_1} = x_1^2;{y_2} = x_2^2$.
Theo hệ thức Vi-et: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = 2m - 3\end{array} \right.$
Xét ${y_1} + {y_2} < 9$$ \Leftrightarrow x_1^2 + x_2^2 < 9 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} < 9 \Leftrightarrow 4{m^2} - 4m + 6 - 9 < 0$$ \Leftrightarrow 4{m^2} - 4m - 3 < 0 \Leftrightarrow \left( {2m + 1} \right)\left( {2m - 3} \right) < 0$$ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2m + 1 < 0\\2m - 3 > 0\end{array} \right.\\\left\{ \begin{array}{l}2m + 1 > 0\\2m - 3 < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m < - \dfrac{1}{2}\\m > \dfrac{3}{2}\end{array} \right.\\\left\{ \begin{array}{l}m < - \dfrac{1}{2}\\m < \dfrac{3}{2}\end{array} \right.\end{array} \right. \Rightarrow - \dfrac{1}{2} < m < \dfrac{3}{2}$
Mà $m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1} \right\}$
Vậy có hai giá trị của $m$ thỏa mãn.
Cho đường thẳng \(d\) :\(y = - 3x + 1\) và parabol : \(\left( P \right)\)\(y = m{x^2}\left( {m \ne 0} \right)\). Tìm \(m\) để \(d\) và \(\left( P \right)\) cắt nhau tại hai điểm \(A\) và \(B\) phân biệt và cùng nằm về một phía đối với trục tung.
-
A
$m > - \dfrac{9}{4}$
-
B
$ - \dfrac{9}{4} < m < 0$
-
C
$m < 0$
-
D
$m > \dfrac{9}{4}$
Đáp án của giáo viên lời giải hay : B
Bước 1: Viết phương trình hoành độ giao điểm (*)
Bước 2: Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm cùng một phía với trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm phân biệt cùng dấu$ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\P > 0\end{array} \right.$
Phương trình hoành độ giao điểm $m{x^2} = - 3x + 1 \Leftrightarrow m{x^2} + 3x - 1 = 0\,\left( * \right)$ có $\Delta = 9 + 4m$; $P = {x_1}.{x_2} = \dfrac{{ - 1}}{m}$ với ${x_1};{x_2}$ là hai nghiệm của phương trình (*).
Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm cùng một phía với trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm phân biệt cùng dấu$ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\P > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}4m + 9 > 0\\\dfrac{{ - 1}}{m} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - \dfrac{9}{4}\\m < 0\end{array} \right. \Leftrightarrow - \dfrac{9}{4} < m < 0$
Vậy $ - \dfrac{9}{4} < m < 0$.
Cho parabol $\left( P \right):y = {x^2}$ và $d:y = 2x + 3.$
Tìm tọa độ giao điểm $A,B$ của $\left( P \right)$ và $ d$.
-
A
$A\left( { - 1; - 1} \right);B\left( {3; - 9} \right)$
-
B
$A\left( { - 1;1} \right);B\left( { - 3;9} \right)$
-
C
$A\left( { - 1;1} \right);B\left( {3;9} \right)$
-
D
$A\left( { - 1; - 1} \right);B\left( {3;9} \right)$
Đáp án của giáo viên lời giải hay : C
Giải phương trình hoành độ giao điểm tìm được hoành độ $x$, thay trở lại hàm số tìm được $y$ từ đó giao điểm có tọa độ $\left( {x;y} \right)$.
Phương trình hoành độ giao điểm ${x^2} = 2x + 3 \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow \left( {x + 1} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \Rightarrow y = {\left( { - 1} \right)^2} = 1\\x = 3 \Rightarrow y = {3^2} = 9\end{array} \right.$
Giao điểm của $d$ và $\left( P \right)$ là $A\left( { - 1;1} \right);B\left( {3;9} \right)$.
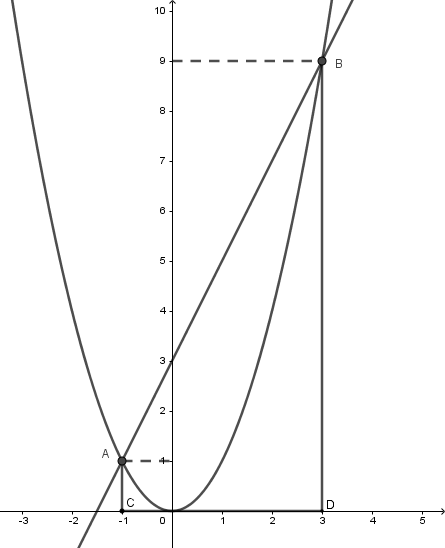
Với giao điểm $A,B$ của $\left( P \right)$ và $d$ ở câu trước . Gọi $C,D$ lần lượt là hình chiếu vuông góc của $A,B$ lên $Ox$. Tính diện tích tứ giác ${\rm{ABDC}}$.
-
A
${S_{ABDC}} = 20\,\,$(đvdt)
-
B
${S_{ABDC}} = 40\,$(đvdt)
-
C
${S_{ABDC}} = 10\,\,$(đvdt)
-
D
${S_{ABDC}} = 30\,\,$(đvdt)
Đáp án của giáo viên lời giải hay : A
+) Vẽ hình trên cùng một hệ trục tọa độ
+) Xác định tọa độ $C,D$
+) Tính diện tích hình thang vuông ${\rm{ABCD}}$. Sử dụng công thức tính độ dài $A\left( {{x_A};{y_A}} \right);B\left( {{x_B};{y_B}} \right) \Rightarrow AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} $
Ta có $A\left( { - 1;1} \right);B\left( {3;9} \right)$ nên $C\left( { - 1;0} \right);D\left( {3;0} \right)$
$ \Rightarrow AC = \sqrt {{0^2} + {{\left( { - 1} \right)}^2}} = 1;$
$DC = 4;BD = \sqrt {{0^2} + {9^2}} = 9.$
Vì $AC \bot BC;BD \bot BC \Rightarrow ABDC$ là hình thang vuông nên ${S_{ABDC}} = \dfrac{{\left( {AC + BD} \right).DC}}{2} = 20$ (đvdt)
Tìm giá trị của tham số $m$ để đường thẳng $d:y = - \dfrac{1}{2}x + m$ và parabol $\left( P \right):y = - \dfrac{1}{4}{x^2}$ cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn \(3{x_1} + 5{x_2} = 5\)
-
A
$m = - \dfrac{5}{{16}}$
-
B
$m = \dfrac{5}{{16}}$
-
C
$m = - \dfrac{5}{4}$
-
D
$m = \dfrac{5}{4}$
Đáp án của giáo viên lời giải hay : A
Bước 1: Viết phương trình hoành độ giao điểm (*)
Bước 2: Tìm điều kiện để đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt
Bước 3: Sử dụng hệ thức Vi-et kết hợp với phương trình đã cho để tìm $m$.
Phương trình hoành độ giao điểm $ - \dfrac{1}{4}{x^2} = - \dfrac{1}{2}x + m \Leftrightarrow {x^2} - 2x + 4m = 0$ có $\Delta ' = 1 - 4m$
Để đường thẳng $d$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thì $\Delta > 0 \Leftrightarrow 1 - 4m > 0 \Leftrightarrow m < \dfrac{1}{4}$
Theo hệ thức Vi-et ta có $\left\{ \begin{array}{l}{x_1} + {x_2} = 2\,\left( 1 \right)\\{x_1}.{x_2} = 4m\,\left( 2 \right)\end{array} \right.$
Ta có \(3{x_1} + 5{x_2} = 5\)$ \Leftrightarrow {x_1} = \dfrac{{5 - 5{x_2}}}{3}$ thay vào phương trình $\left( 1 \right)$ ta được $\dfrac{{5 - 5{x_2}}}{3} + {x_2} = 2 \Leftrightarrow {x_2} = - \dfrac{1}{2} \Rightarrow {x_1} = \dfrac{5}{2}$
Thay ${x_2} = - \dfrac{1}{2};{x_1} = \dfrac{5}{2}$ vào phương trình $\left( 2 \right)$ ta được $\left( { - \dfrac{1}{2}} \right).\dfrac{5}{2} = 4m \Leftrightarrow m = - \dfrac{5}{{16}}$ (TM )
Vậy $m = - \dfrac{5}{{16}}$ là giá trị cần tìm.
Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(d:y = \left( {{m^2} + 2} \right)x - {m^2}\). Tìm \(m\) để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về bên phải trục tung.
-
A
\(m > 0\)
-
B
\(m \in R\)
-
C
\(m \ne 0\)
-
D
\(m < 0\)
Đáp án của giáo viên lời giải hay : C
- Xét phương trình hoành độ giao điểm của \(d\) và \(\left( P \right)\)..
- Điều kiện để hai giao điểm nằm về bên phải trục tung là phương trình có hai nghiệm phân biệt cùng dương \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right..\)
Xét phương trình hoành độ giao điểm \({x^2} = \left( {{m^2} + 2} \right)x - {m^2} \Leftrightarrow {x^2} - \left( {{m^2} + 2} \right)x + {m^2} = 0\left( 1 \right)\).
\(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về bên phải trục tung khi và chỉ khi phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt cùng dương
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\Delta = {\left( {{m^2} + 2} \right)^2} - 4{m^2} > 0\\S = {m^2} + 2 > 0\\P = {m^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {{m^2} - 2m + 2} \right)\left( {{m^2} + 2m + 2} \right) > 0\\m \ne 0\end{array} \right.\)
Mà \({m^2} - 2m + 2 = {\left( {m - 1} \right)^2} + 1 > 0\,\,\forall m;\)\({m^2} + 2m + 2 = {\left( {m + 1} \right)^2} + 1 > 0\,\,\forall m\) nên \(\left( {{m^2} - 2m + 2} \right)\left( {{m^2} + 2m + 2} \right) > 0;\,\forall m\)
Từ đó \(m \ne 0\) thỏa mãn đề bài.
Cho parabol \(\left( P \right)\) có đỉnh \(O\) và đi qua điểm \(A\left( {2;4} \right)\) và đường thẳng \(\left( d \right):y = 2(m - 1)x + 2m + 2\) (với \(m\) là tham số). Giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt là
-
A
\(m > 2 + \sqrt 5 \)
-
B
\(m < 2 - \sqrt 5 \)
-
C
\(\left[ \begin{array}{l}m > 2 + \sqrt 5 \\m < 2 - \sqrt 5 \end{array} \right.\)
-
D
Với mọi \(m\)
Đáp án của giáo viên lời giải hay : D
Viết phương trình parabol khi biết điểm đi qua
Sử dụng biện luận phương trình bậc hai để biện luận số giao điểm của hai đồ thị thông qua phương trình hoành độ giao điểm
Parabol \(\left( P \right)\) có đỉnh \(O\) nên có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
Mà \(\left( P \right)\) đi qua điểm \(A\left( {2;4} \right)\) nên toạ độ \(A\) thoả mãn phương trình parabol \(\left( P \right)\) suy ra \(4 = a{.2^2} = 4a \Leftrightarrow a = 1\) (thoả mãn \(a \ne 0\))
Phương trình parabol \(\left( P \right)\) là \(y = {x^2}\).
\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt.
Suy ra phương trình \({x^2} - 2(m - 1)x - 2m - 2 = 0\) có hai nghiệm phân biệt.
\( \Leftrightarrow \Delta ' = {( - (m - 1))^2} + 2m + 2 > 0\)\( \Leftrightarrow {m^2} - 2m + 1 + 2m + 2 > 0\)\( \Leftrightarrow {m^2} + 3 > 0\) (luôn đúng)
Vậy \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.
Cho parabol \(\left( P \right):y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( { - 2;4} \right)\) và tiếp xúc với đồ thị \(\left( d \right)\) của hàm số \(y = 2(m - 1)x - (m - 1)\).Toạ độ tiếp điểm là
-
A
\(\left( {0;0} \right)\)
-
B
\(\left( {1;1} \right)\)
-
C
A và B đúng
-
D
Đáp án khác
Đáp án của giáo viên lời giải hay : C
Viết phương trình parabol khi biết điểm đi qua
Sử dụng biện luận phương trình bậc hai để biện luận số giao điểm của hai đồ thị thông qua phương trình hoành độ giao điểm
\(\left( P \right)\) đi qua điểm \(A\left( { - 2;4} \right)\) nên \(4 = a.{\left( { - 2} \right)^2} = 4a \Leftrightarrow a = 1\).
Vậy phương trình parabol \(\left( P \right)\) là \(y = {x^2}\).
Để \(\left( P \right)\) tiếp xúc với \(\left( d \right)\) thì phương trình hoành độ giao điểm \({x^2} - 2(m - 1)x + (m - 1) = 0\) có nghiệm kép
\( \Leftrightarrow \Delta ' = {( - (m - 1))^2} - m + 1 = 0\)\( \Leftrightarrow {m^2} - 2m + 1 - m + 1 = 0\)\( \Leftrightarrow {m^2} - 3m + 2 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\)
Nếu \(m = 1\) thì hoành độ giao điểm là \(x = 0\) . Vậy tiếp điểm \(\left( {0;0} \right)\)
Nếu \(m = 2\) thì hoành độ giao điểm là \(x = 1\) . Vậy tiếp điểm \(\left( {1;1} \right)\)
