Trong các cách viết sau đây, cách viết nào cho ta phân số:
-
A
\(\dfrac{{12}}{0}\)
-
B
\(\dfrac{{ - 4}}{5}\)
-
C
\(\dfrac{3}{{0,25}}\)
-
D
\(\dfrac{{4,4}}{{11,5}}\)
Đáp án của giáo viên lời giải hay : B
Dựa vào định nghĩa phân số: \(\dfrac{a}{b}\) là phân số với \(a,b \in \mathbb{Z},\,b \ne 0\).
+) \(\dfrac{{12}}{0}\) không là phân số vì mẫu số bằng $0.$
+) \(\dfrac{3}{{0,25}}\) không là phân số vì mẫu số là số thập phân.
+) \(\dfrac{{4,4}}{{11,5}}\) không là phân số vì tử số và mẫu số là số thập phân.
+) \(\dfrac{{ - 4}}{5}\) là phân số vì \( - 4;\,5\, \in \mathbb{Z} \) và mẫu số là $5$ khác $0.$
Phần tô màu trong hình sau biểu diễn phân số nào?

-
A
\(\dfrac{1}{2}\)
-
B
\(\dfrac{1}{4}\)
-
C
\(\dfrac{3}{4}\)
-
D
\(\dfrac{5}{8}\)
Đáp án của giáo viên lời giải hay : B
Quan sát hình vẽ, đếm số ô vuông có trong hình và số ô vuông được tô màu, phân số biểu thị có tử là số ô vuông tô màu và mẫu là tổng số ô vuông có trong hình.
Trong hình có \(2\) ô vuông tô màu và tổng tất cả \(8\) ô vuông nên phân số biểu thị là \(\dfrac{2}{8} = \dfrac{1}{4}\)
Chọn câu sai?
-
A
\(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
-
B
\(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
-
C
\(\dfrac{{ - 4}}{{15}} = \dfrac{{ - 16}}{{ - 60}}\)
-
D
\(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
Đáp án của giáo viên lời giải hay : C
Kiểm tra tính đúng sai của từng đáp án bằng cách sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Đáp án A: Vì \(1.135 = 3.45\) nên \(\dfrac{1}{3} = \dfrac{{45}}{{135}}\)
\( \Rightarrow A\) đúng.
Đáp án B: Vì \(\left( { - 13} \right).\left( { - 40} \right) = 20.26\) nên \(\dfrac{{ - 13}}{{20}} = \dfrac{{26}}{{ - 40}}\)
\( \Rightarrow B\) đúng.
Đáp án C: Vì \(\left( { - 4} \right).\left( { - 60} \right) \ne 15.\left( { - 16} \right)\) nên \(\dfrac{{ - 4}}{{15}} \ne \dfrac{{ - 16}}{{ - 60}}\)
\( \Rightarrow C\) sai.
Đáp án D: Vì \(6.\left( { - 49} \right) = 7.\left( { - 42} \right)\) nên \(\dfrac{6}{7} = \dfrac{{ - 42}}{{ - 49}}\)
\( \Rightarrow D\) đúng.
Điền số thích hợp vào chỗ chấm $\dfrac{{15}}{{90}} = \dfrac{5}{{...}}$
-
A
\(20\)
-
B
\( - 60\)
-
C
\(60\)
-
D
\(30\)
Đáp án của giáo viên lời giải hay : D
Sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
\(\begin{array}{l}\dfrac{{15}}{{90}} = \dfrac{5}{x}\\15.x = 90.5\\x = \dfrac{{90.5}}{{15}}\\x = 30\end{array}\)
Vậy số cần điền là \(30\)
Cho biểu thức \(C = \dfrac{{11}}{{2n + 1}}\) . Tìm tất cả các giá trị của $n$ nguyên để giá trị của $C$ là một số tự nhiên.
-
A
\(n \in \left\{ { - 6; - 1;0;5} \right\}\)
-
B
\(n \in \left\{ { - 1;5} \right\}\)
-
C
\(n \in \left\{ {0;5} \right\}\)
-
D
\(n \in \left\{ {1;11} \right\}\)
Đáp án của giáo viên lời giải hay : C
- $C$ là số tự nhiên suy ra \(C\) là số nguyên hay $2n + 1$ là ước của $11$
- Từ đó tìm các giá trị của $n$ rồi thử lại kiểm tra lại điều kiện \(C\) là số tự nhiên.
Vì \(C \in N\) nên \(C \in Z.\) Do đó ta tìm \(n \in Z\) để \(C \in Z\)
Vì \(n \in Z\) nên để \(C \in Z\) thì \(2n + 1 \in U\left( {11} \right) = \left\{ { \pm 1; \pm 11} \right\}\)
Ta có bảng:

Vì \(C \in N\) nên ta chỉ nhận các giá trị \(n = 0;n = 5\)
Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.
-
A
\(1\)
-
B
\(0\)
-
C
\(2\)
-
D
\(3\)
Đáp án của giáo viên lời giải hay : A
Phân số \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\) là một số nguyên nếu \(b\) là ước của $a$
Vì \(n\) nguyên dương nên để \(\dfrac{9}{{4n + 1}}\) nguyên thì \(4n + 1 \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)
Ta có bảng:
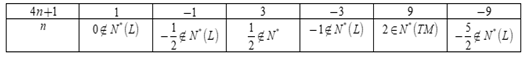
Vậy có duy nhất một giá trị của \(n\) thỏa mãn là \(n = 2\)
Tổng các số \(a;b;c\) thỏa mãn \(\dfrac{6}{9} = \dfrac{{12}}{a} = \dfrac{b}{{ - 54}} = \dfrac{{ - 738}}{c}\) là:
-
A
\(1161\)
-
B
\( - 1125\)
-
C
\( - 1053\)
-
D
\(1089\)
Đáp án của giáo viên lời giải hay : B
Sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Ta có: \(\dfrac{6}{9} = \dfrac{{12}}{a} \Rightarrow 6.a = 9.12\) \( \Rightarrow a = \dfrac{{9.12}}{6} = 18\)
\(\dfrac{6}{9} = \dfrac{b}{{ - 54}} \Rightarrow 6.\left( { - 54} \right) = 9.b\) \( \Rightarrow b = \dfrac{{6.\left( { - 54} \right)}}{9} = - 36\)
\(\dfrac{6}{9} = \dfrac{{ - 738}}{c} \Rightarrow 6.c = 9.\left( { - 738} \right)\) \( \Rightarrow c = \dfrac{{9.\left( { - 738} \right)}}{6} = - 1107\)
Vậy \(a + b + c\) \( = 18 + \left( { - 36} \right) + \left( { - 1107} \right) = - 1125\)
Cho các phân số: \(\dfrac{{15}}{{60}};\dfrac{{ - 7}}{5};\dfrac{6}{{15}};\dfrac{{28}}{{ - 20}};\dfrac{3}{{12}}\)
Số cặp phân số bằng nhau trong những phân số trên là:
-
A
\(4\)
-
B
\(1\)
-
C
\(3\)
-
D
\(2\)
Đáp án của giáo viên lời giải hay : D
- Ta sẽ chia các phân số thành \(2\) loại: phân số dương, phân số âm (chú ý phân số dương và phân số âm không thể bằng nhau)
- Tìm các cặp phân số bằng nhau trong những phân số dương và các cặp phân số bằng nhau trong những phân số âm rồi kết luận.
Sử dụng kiến thức:
- Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
- Định nghĩa các phân số dương, phân số âm:
+ Phân số âm: là phân số có tử và mẫu là các số nguyên trái dấu.
+ Phân số dương: là phân số có tử và mẫu là các số nguyên cùng dấu.
- Các phân số dương: \(\dfrac{{15}}{{60}};\dfrac{6}{{15}};\dfrac{3}{{12}}\)
+ Vì \(15.15 \ne 60.6\) nên \(\dfrac{{15}}{{60}} \ne \dfrac{6}{{15}}\)
+ Vì \(6.12 \ne 15.3\) nên \(\dfrac{6}{{15}} \ne \dfrac{3}{{12}}\)
+ Vì \(15.12 = 60.3\) nên \(\dfrac{{15}}{{60}} = \dfrac{3}{{12}}\)
- Các phân số âm: \(\dfrac{{ - 7}}{5};\dfrac{{28}}{{ - 20}}\)
Vì \(\left( { - 7} \right).\left( { - 20} \right) = 5.28\) nên \(\dfrac{{ - 7}}{5} = \dfrac{{28}}{{ - 20}}\)
Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.
Tính tổng các giá trị \(x \in Z\) biết rằng \( - \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}.\)
-
A
\(22\)
-
B
\(20\)
-
C
\(18\)
-
D
\(15\)
Đáp án của giáo viên lời giải hay : C
Tính giá trị các phân số rồi tìm các số nguyên \(x\) thỏa mãn.
Ta có:
\(\begin{array}{l} - \dfrac{{111}}{{37}} < x < \dfrac{{91}}{{13}}\\ \Rightarrow - 3 < x < 7\\ \Rightarrow x \in \left\{ { - 2; - 1;0;1;2;3;4;5;6} \right\}\end{array}\)
Vậy tổng các giá trị của \(x\) thỏa mãn là: \(\left( { - 2} \right) + \left( { - 1} \right) + ... + 5 + 6 = 18\)
Tìm tập hợp các số nguyên \(n\) để \(A = \dfrac{{3n - 5}}{{n + 4}}\) có giá trị là số nguyên.
-
A
\(n \in \left\{ {13} \right\}\)
-
B
\(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
-
C
\(n \in \left\{ { - 17; - 1;1;17} \right\}\)
-
D
\(n \in \left\{ { - 13; - 3;3;13} \right\}\)
Đáp án của giáo viên lời giải hay : B
- Biến đổi \(A\) về dạng \(A = a + \dfrac{b}{{n + 4}}\) với \(a,b \in Z\)
- Để \(A\) nguyên thì \(n + 4 \in U\left( b \right)\)
Ta có:
\(A = \dfrac{{3n - 5}}{{n + 4}} = \dfrac{{3n + 12 - 12 - 5}}{{n + 4}}\)\( = \dfrac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\) \( = \dfrac{{3\left( {n + 4} \right)}}{{n + 4}} + \dfrac{{ - 17}}{{n + 4}} = 3 + \dfrac{{ - 17}}{{n + 4}}\)
Vì \(n \in Z\) nên để \(A \in Z\) thì \(n + 4 \in U\left( { - 17} \right) = \left\{ { \pm 1; \pm 17} \right\}\)
Ta có bảng:
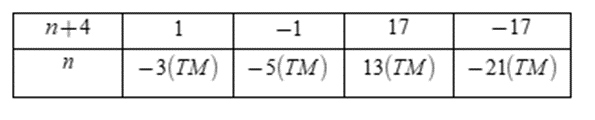
Vậy \(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\dfrac{x}{5} = \dfrac{3}{y}\) và \(x > y?\)
-
A
\(4\)
-
B
\(3\)
-
C
\(2\)
-
D
\(1\)
Đáp án của giáo viên lời giải hay : A
Sử dụng kiến thức:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Ta có: \(\dfrac{x}{5} = \dfrac{3}{y}\)\( \Rightarrow x.y = 5.3 = 15\)
Mà \(15 = 5.3 = 15.1 = \left( { - 3} \right).\left( { - 5} \right) = \left( { - 1} \right).\left( { - 15} \right)\) và \(x,y \in Z,x > y\) nên \(\left( {x;y} \right) \in \left\{ {\left( {5;3} \right),\left( {15;1} \right),\left( { - 3; - 5} \right),\left( { - 1; - 15} \right)} \right\}\)
Tìm \(x;y\) biết \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) và \(x - y = 5.\)
-
A
\(x = 15;y = 5\)
-
B
\(x = 5;y = 15\)
-
C
\(x = 20;y = 15\)
-
D
\(x = 25;y = 10\)
Đáp án của giáo viên lời giải hay : C
- Rút \(x\) theo \(y\) từ điều kiện đơn giản rồi thay vào đẳng thức hai phân số bằng nhau.
- Sử dụng kiến thức hai phân số bằng nhau để tìm \(y,\) từ đó suy ra \(x\)
- Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau)
Ta có: \(x - y = 5 \Rightarrow x = y + 5\) thay vào \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) ta được:
\(\begin{array}{l}\dfrac{{y + 5 - 4}}{{y - 3}} = \dfrac{4}{3}\\\dfrac{{y + 1}}{{y - 3}} = \dfrac{4}{3}\\3\left( {y + 1} \right) = 4\left( {y - 3} \right)\\3y + 3 = 4y - 12\\3y - 4y = - 12 - 3\\ - y = - 15\\y = 15\\ \Rightarrow x = 15 + 5 = 20\end{array}\)
Vậy \(x = 20;y = 15\)
Viết số nguyên \( - 16\) dưới dạng phân số ta được:
-
A
\(\dfrac{{ - 16}}{0}\)
-
B
\(\dfrac{{16}}{1}\)
-
C
\(\dfrac{{ - 16}}{1}\)
-
D
\(\dfrac{{16}}{0}\)
Đáp án của giáo viên lời giải hay : C
Viết số nguyên \( - 16\) dưới dạng phân số ta được: \(\dfrac{{ - 16}}{1}\)
Cách viết nào sau đây cho ta một phân số:
-
A
\(\dfrac{4}{0}\)
-
B
\(\dfrac{{1,5}}{3}\)
-
C
\(\dfrac{0}{7}\)
-
D
\(\dfrac{{ - 5}}{{3,5}}\)
Đáp án của giáo viên lời giải hay : C
+ \(\dfrac{4}{0}\) có mẫu bằng \(0\) nên không là phân số
+ \(\dfrac{{1,5}}{3}\) có \(1,5 \notin \mathbb{Z}\) nên không là phân số
+ \(\dfrac{0}{7}\) là phân số
+ \(\dfrac{{ - 5}}{{3,5}}\) có \(3,5 \notin \mathbb{Z}\) nên không là phân số
