
Điền số thích hợp vào ô trống:
\(65\) phút \(:\,\,5\,\, = \,\)
phút.
\(65\) phút \(:\,\,5\,\, = \,\)
phút.
Thực hiện phép chia các số tự nhiên, sau đó ghi thêm đơn vị đo vào kết quả.
Ta có: \(65\) phút \(:\,\,5\,\, = \,\,13\) phút
Vậy đáp án đúng điền vào ô trống là \(13\)

Điền số thích hợp vào ô trống:
\(10\) phút \(8\) giây \(:\,2\, = \,\)
phút
giây.
\(10\) phút \(8\) giây \(:\,2\, = \,\)
phút
giây.
- Ta đặt tính như đối với phép chia các số tự nhiên.
- Chia từng số đo ở số bị chia cho số chia (theo thứ tự từ trái sang phải).
- Cách chia:
+ Lấy \(10\) phút $:{\rm{ 2 }} = {\rm{ 5}}$ phút và không dư;
+ Lấy \(8\) giây $:{\rm{ 2 }} = {\rm{ 4}}$ giây và không dư.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
Ta đặt tính và thực hiện tính như sau:

Vậy: \(10\) phút \(8\) giây \(:\,\,2\,\, = \,\,5\) phút \(4\) giây.
Đáp án đúng điền vào ô trồng lần lượt từ trái sang phải là \(5\,;\,\,4\).

Điền số thích hợp vào ô trống:
\(21\) giờ \(12\) phút $:\,\,\,4\,\, = \;$
giờ
phút
\(21\) giờ \(12\) phút $:\,\,\,4\,\, = \;$
giờ
phút
- Ta đặt tính như đối với phép chia các số tự nhiên.
- Chia từng số đo ở số bị chia cho số chia (theo thứ tự từ trái sang phải).
- Cách chia:
+ Lấy \(21\) giờ $:{\rm{ }}4{\rm{ }} = {\rm{ 5}}$ giờ và còn dư \(1\) giờ;
+ Đổi \(1\) giờ $ = {\rm{ 60}}$ phút rồi cộng thêm \(12\) phút ở số bị chia ta được \(72\) phút và chia tiếp cho \(4\).
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
Ta đặt tính và thực hiện tính như sau:

Vậy \(21\) giờ \(12\) phút $:\,4\, = \,$ \(5\) giờ \(18\) phút.
Đáp án đúng điền vào ô trồng lần lượt từ trái sang phải là \(5\,;\,\,18\).

Tính: \(14\) ngày \(6\) giờ $:{\rm{ }}9$.
A. \(1\) ngày \(14\) giờ
B. \(1\) ngày \(12\) giờ
C. \(1\) ngày \(8\) giờ
D. \(1\) ngày \(16\) giờ
A. \(1\) ngày \(14\) giờ
- Ta đặt tính như đối với phép chia các số tự nhiên.
- Chia từng số đo của số bị chia cho số chia (theo thứ tự từ trái sang phải).
- Cách chia:
+ Lấy \(14\) ngày $:{\rm{ }}9{\rm{ }} = {\rm{ }}1$ ngày và còn dư \(5\) ngày;
+ Đổi \(5\) ngày $ = {\rm{ 120}}$ giờ và cộng thêm \(6\) giờ ở số bị chia ta được \(126\) giờ rồi chia tiếp cho \(9\).
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
Ta đặt tính và thực hiện tính như sau:

Vậy: \(14\) ngày \(6\) giờ $:{\rm{ }}9$ \( = \,1\) ngày \(14\) giờ.

Tính : \(19,2\) giờ \(:\,3\).
A. \(5,4\) giờ
B. \(6,4\) giờ
C. \(54\) giờ
D. \(54\) giờ
B. \(6,4\) giờ
- Đặt tính và thực hiện tính như đối với phép chia một số thập phân cho một số tự nhiên.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
Đặt tính và thực hiện tính ta có:
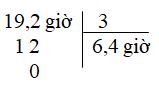
Vậy \(19,2\) giờ \(:\,3\,= \,6,4\) giờ.

Điền số thích hợp vào ô trống:
\(32\) phút \(16\) giây \( \times \,\,3\,\,:\,\,4\,\, = \,\,\,\)
phút
giây
\(32\) phút \(16\) giây \( \times \,\,3\,\,:\,\,4\,\, = \,\,\,\)
phút
giây
- Thực hiện tính giá trị biểu thức như đối với các số tự nhiên. Trong biểu thức chỉ có phép nhân và phép chia nên ta tính lần lượt từ trái sang phải.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
Ta có:
\(32\) phút \(16\) giây \( \times \,\,3\,\,:\,\,4\,\)
\( = 96\) phút \(48\) giây \(\,:\,\,4\,\)
\( = 24\) phút \(12\) giây
Vây \(32\) phút \(16\) giây \( \times \,\,3\,\,:\,\,4\,\, = \,\,\,24\) phút \(12\) giây
Đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(24\,;\,\,12\).

Tính: \((4\) giờ \(36\) phút \( + \,\,18\) phút\()\,:\,3\).
A. \(1\) giờ \(36\) phút
B. \(1\) giờ \(38\) phút
C. \(4\) giờ \(54\) phút
D. \(4\) giờ \(42\) phút
B. \(1\) giờ \(38\) phút
- Ta thực hiện tính giá trị biểu thức như đối với các số tự nhiên, tính lần lượt trong ngoặc trước ngoài ngoặc sau.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
- Trong khi tính, nếu số phút lớn hơn hoặc bằng \(60\) thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của phút là giờ.
Ta có:
\((4\) giờ \(36\) phút \( + \,18\) phút \()\,:\,3\)
\( = \,\,4\) giờ \(54\) phút \(\,:\,3\)
\( = \,\,3\) giờ \(114\) phút \(\,:\,3\)
\( = \,\,1\) giờ \(38\) phút

Điền số thích hợp vào ô trống:
Một đu quay quay \(5\) vòng hết \(6\) phút \(20\) giây. Vậy đu quay đó quay \(1\) vòng hết
phút
giây.
Một đu quay quay \(5\) vòng hết \(6\) phút \(20\) giây. Vậy đu quay đó quay \(1\) vòng hết
phút
giây.
Tính thời gian đu quay quay \(1\) vòng ta lấy thời gian đu quay quay \(5\) vòng chia cho \(5\).
Đu quay đó quay \(1\) vòng hết số thời gian là:
\(6\) phút \(20\) giây \(:\,\,5\,\, = \,\,1\) phút \(16\) giây
Đáp số: \(1\) phút \(16\) giây
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(1;\,\,16\).

Lan gấp hoa từ \(8\) giờ \(12\) phút đến \(8\) giờ \(40\) phút được \(8\) bông hoa. Hỏi trung bình Lan gấp \(1\) bông hoa trong thời gian bao lâu?
A. \(3,5\) phút
B. \(4,5\) phút
C. \(28\) phút
D. \(40\) phút
A. \(3,5\) phút
- Tính thời gian Lan gấp được \(8\) bông hoa, tức là tính \(8\) giờ \(40\) phút \( - \,8\) giờ \(12\) phút.
- Tính thời gian Lan gấp được \(1\) bông hoa ta lấy thời gian Lan gấp được \(8\) bông hoa chia cho \(8\).
Lan gấp được \(8\) bông hoa trong số thời gian là:
\(8\) giờ \(40\) phút \( - \,8\) giờ \(12\) phút \( = \,28\) phút
Lan gấp được \(1\) bông hoa trong số thời gian là:
\(28:8 = 3,5\) (phút)
Đáp số: \(3,5\) phút.

Một người thợ làm xong \(5\) sản phẩm trong $18$ giờ $35$ phút. Hỏi người đó làm xong 8 sản phẩm như thế trong bao lâu?
A. \(21\) giờ \(43\) phút
B. \(24\) giờ \(44\) phút
C. \(28\) giờ \(23\) phút
D. \(29\) giờ \(44\) phút
D. \(29\) giờ \(44\) phút
- Tìm thời gian người đó làm xong $1$ sản phẩm (Đây là bước rút về đơn vị) ta lấy thời gian làm xong \(5\) sản phẩm chia cho \(5\).
- Tìm thời gian người đó làm xong $8$ sản phẩm ta lấy thời gian làm xong $1$ sản phẩm nhân với \(8\).
- Nếu số phút lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của phút là giờ.
Thời gian người đó làm xong \(1\) sản phẩm là:
$18$ giờ $35$ phút$\;:\,\,5\,\, = \,\,3$ giờ $43$ phút
Thời gian người đó làm xong \(8\) sản phẩm là:
$\,3$ giờ $43$ phút \( \times \,\,8\,\, = \,24\) giờ \(344\) phút \( = \,\,29\) giờ \(44\) phút (vì $344$ phút \( = \,\,5\) giờ \(44\) phút)
Đáp số: \(29\) giờ \(44\) phút.

Điền dấu (\(>;\,<;\, =\)) thích hợp vào ô trống:
\(21\) giờ $24$ phút $:\,\,6$
$15$ giờ $:\,\,4$
\(21\) giờ $24$ phút $:\,\,6$
$15$ giờ $:\,\,4$
- Tính kết quả \(2\) vế và đưa về cùng đơn vị.
- So sánh kết quả của \(2\) vế để chọn dấu phù hợp.
Ta có: \(21\) giờ $24$ phút $:\,\,6\,\, = \,\,3$ giờ \(34\) phút
$15$ giờ $:\,\,4\,\, = \,\,3,75$ giờ $ = \,3$ giờ \(45\) phút
Mà $3$ giờ \(34\) phút $ < \,3$ giờ \(45\) phút
Nên: \(21\) giờ $24$ phút $:\,\,6$ $ < \,\,15$ giờ $:\,\,4$.

Máy thứ nhất sản xuất ra \(10\) dụng cụ trong \(1\) giờ \(20\) phút. Máy thứ hai sản xuất ra \(12\) dụng cụ như thế trong \(1,5\) giờ. Hỏi máy nào sản xuất \(1\) dụng cụ nhanh hơn và nhanh hơn bao nhiêu thời gian?
A. Máy thứ nhất; \(5\) phút
B. Máy thứ nhất; \(0,5\) phút
C. Máy thứ hai; \(5\) phút
D. Máy thứ hai; \(0,5\) phút
D. Máy thứ hai; \(0,5\) phút
- Đổi \(1\) giờ \(20\) phút và \(1,5\) giờ sang đơn vị đo là phút.
- Tìm thời gian máy thứ nhất sản xuất \(1\) dụng cụ = thời gian sản xuất ra \(10\) dụng cụ \(:\,10\).
- Tìm thời gian máy thứ hai sản xuất \(1\) dụng cụ = thời gian sản xuất ra \(12\) dụng cụ \(:\,12\).
- So sánh thời gian sản xuất \(1\) dụng cụ của máy nào nhỏ hơn thì máy đó sản xuất \(1\) dụng cụ nhanh hơn.
- Tính thời gian nhanh hơn ta lấy thời gian lớn hơn trừ đi thời gian nhỏ hơn.
Đổi: \(1\) giờ \(20\) phút $ = 80$ phút; \(1,5\) giờ \( = 90\) phút.
Máy thứ nhất sản xuất \(1\) dụng cụ trong số phút là:
$80:10 = 8$ (phút)
Máy thứ hai sản xuất \(1\) dụng cụ trong số phút là
$90:12 = 7,5$ (phút)
Ta có: \(8\) phút \( > 7,5\) phút nên máy thứ hai sản xuất \(1\) dụng cụ nhanh hơn và nhanh hơn số thời gian là:
\(8\) phút \( - \,7,5\,\) phút \(= \,0,5\) (phút)
Đáp số: Máy thứ hai; \(0,5\) phút.

Điền số thích hợp vào ô trống:
Một đội công nhân chuyển gạo vào \(2\) kho với thời gian chuyển vào kho thứ nhất là \(5\) giờ \(15\) phút.
Thời gian chuyển gạo vào kho thứ hai nhanh gấp \(3\) lần so với kho thứ nhất.
Vậy tổng thời gian chuyển gạo vào cả hai kho là
giờ.
Một đội công nhân chuyển gạo vào \(2\) kho với thời gian chuyển vào kho thứ nhất là \(5\) giờ \(15\) phút.
Thời gian chuyển gạo vào kho thứ hai nhanh gấp \(3\) lần so với kho thứ nhất.
Vậy tổng thời gian chuyển gạo vào cả hai kho là
giờ.
Thời gian chuyển gạo vào kho thứ hai nhanh gấp \(3\) lần thời gian chuyển vào kho thứ nhất nghĩa là để chuyển vào kho thứ hai đội công nhân cần số thời gian ít hơn \(3\) lần thời gian chuyển vào kho thứ nhất.
Để giải bài này ta có thể làm như sau:
- Tìm thời gian chuyển gạo vào kho thứ hai ta lấy thời gian chuyển vào kho thứ nhất chia cho \(3\).
- Tìm thời gian chuyển gạo vào 2 kho ta tìm tổng thời gian chuyển vào kho thứ nhất và thời gian chuyển vào kho thứ hai.
Thời gian chuyển gạo vào kho thứ hai là:
\(5\) giờ \(15\) phút \(:\,3\, = \,1\) giờ $45$ phút
Thời gian chuyển gạo vào cả hai kho là:
\(5\) giờ \(15\) phút \( + \,1\) giờ \(45\) phút \(\, = \,6\) giờ \(60\) phút \(\, = \,7\) giờ
Đáp số: \(\,7\) giờ.
Vậy đáp án đúng điền vào ô trống là \(7\).

Thời gian từ bắt đầu ngày đến bây giờ bằng \(\dfrac{2}{3}\) thời gian từ bây giờ cho đến bắt đầu ngày tiếp theo. Hỏi bây giờ là mấy giờ?
A. \(8\) giờ \(30\) phút
B. \(9\) giờ \(15\) phút
C. \(9\) giờ \(36\) phút
D. \(10\) giờ \(10\) phút
C. \(9\) giờ \(36\) phút
Ta có \(1\) ngày \( = \,24\) giờ.
Thời gian từ bắt đầu ngày đến bây giờ và thời gian từ bây giờ cho đến bắt đầu ngày tiếp theo chính là \(1\) ngày và bằng \(24\) giờ.
Khi đó ta có bài toán tìm hai số khi biết tổng và tỉ số của hai số đó, ta vẽ sơ đồ và tìm được thời gian từ bắt đầu ngày đến bây giờ.
Ta có \(1\) ngày \( = \,\,24\) giờ
Thời gian từ bắt đầu ngày đến bây giờ và thời gian từ bây giờ cho đến bắt đầu ngày tiếp theo chính là \(1\) ngày và bằng \(24\) giờ.
Ta có sơ đồ:
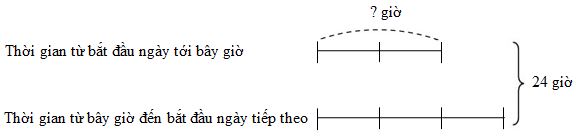
Theo sơ đồ, tổng số phần bằng nhau là:
\(2 + 3 = 5\) (phần)
Giá trị một phần là:
\(24:5 = 4,8\) (giờ)
Thời gian từ bắt đầu ngày tới bây giờ là:
\(4,8 \times 2 = 9,6\) (giờ)
\(9,6\) giờ \( = \,9\) giờ \(36\) phút
Vậy bây giờ là \(9\) giờ \(36\) phút.
