
Điền số thích hợp vào ô trống:
\(3\) năm =
tháng.
\(3\) năm =
tháng.
Ta có: \(1\) năm \( = \,\,12\) tháng . Để đổi số đo thời gian từ năm sang tháng ta chỉ cần lấy \(12\) tháng nhân với số đó.
Ta có: \(1\) năm \( = \,\,12\) tháng.
Do đó: \(3\) năm \( = \,\,12\) tháng \( \times \,\,3\,\, = \,\,36\) tháng.
Vậy đáp án đúng điền vào ô trống là \(36\).

Tháng hai (không phải năm nhuận) có bao nhiêu ngày?
A. \(28\) ngày
B. \(29\) ngày
C. \(30\) ngày
D. \(31\) ngày
A. \(28\) ngày
Xem lại lí thuyết về bảng đơn vị đo thời gian.
Tháng hai có \(28\) ngày, vào năm nhuận có \(29\) ngày.

Điền số thích hợp vào ô trống:
\(2,4\) giờ =
phút
\(2,4\) giờ =
phút
\(1\) giờ $ = \,\,60$ phút. Muốn đổi một số từ đơn vị giờ sang phút ta lấy \(60\) phút nhân với số đó.
Ta có \(1\) giờ $= \,60$ phút.
Do đó: \(2,4\) giờ $ = 60$ phút $ \times \,\,2,4\,\, = \,\,144$ phút.
Vậy đáp án đúng điền vào ô trống là \(144\).

Trong một năm có bao nhiêu tháng có \(31\) ngày?
A. \(4\) tháng
B. \(5\) tháng
C. \(6\) tháng
D. \(7\) tháng
D. \(7\) tháng
Dựa vào bảng đơn vị đo thời gian.
Ta có: tháng một, tháng ba, tháng năm, tháng bảy, tháng tám, tháng mười, tháng mười hai có \(31\) ngày.
Vậy trong một năm có \(7\) tháng có \(31\) ngày.

Điền số thích hợp vào ô trống:
\(6\) năm \(9\) tháng \( + \,\,2\) năm \(2\) tháng =
năm
tháng.
\(6\) năm \(9\) tháng \( + \,\,2\) năm \(2\) tháng =
năm
tháng.
- Đặt tính thẳng hàng và thực hiện tính như đối với phép cộng các số tự nhiên.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
- Nếu số tháng ở kết quả lớn hơn hoặc bằng $12$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn tháng là năm.
Ta đặt tính và thực hiện tính như sau:

Do đó: \(6\) năm \(9\) tháng \( + \,2\) năm \(2\) tháng = \(8\) năm \(11\) tháng.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(8\,;\,\,11\).

Bác Hồ ra đi tìm đường cứu nước ngày \(5\) tháng \(6\) năm \(1911\). Hỏi Bác ra đi tìm đường cứu nước vào thế kỉ nào?
A. Thế kỉ \(XVIII\)
B. Thế kỉ \(XIX\)
C. Thế kỉ \(XX\)
D. Thế kỉ \(XXI\)
C. Thế kỉ \(XX\)
Từ năm \(1\) đến năm $100$ là thế kỉ một ( thế kỉ $I$)
Từ năm $101$ đến năm 200 là thế kỉ hai ( thế kỉ $II$)
...
Từ năm $1801$ đến năm $1900$ là thế kỉ mười chín ( thế kỉ $XIX$)
Từ năm $1901$ đến năm $2000$ là thế kỉ hai mươi ( thế kỉ $XX$)
Từ năm $2001$ đến năm $2100$ là thế kỉ hai mươi mốt ( thế kỉ $XXI$)
Ta có: từ năm $1901$ đến năm $2000$ là thế kỉ hai mươi ( thế kỉ $XX$).
Do đó, Bác Hồ ra đi tìm đường cứu nước năm \(1911\), thuộc thế kỉ $XX$.

Một ca nô đi từ bến sông A lúc \(7\) giờ \(15\) phút và đến bến sông B lúc \(9\) giờ \(10\) phút. Hỏi ca nô đi từ A đến B hết bao nhiêu thời gian? Biết rằng dọc đường ca nô dừng lại nghỉ \(10\) phút.
A. \(1\) giờ \(15\) phút
B. \(1\) giờ \(45\) phút
C. \(1\) giờ \(55\) phút
D. \(2\) giờ \(5\) phút
B. \(1\) giờ \(45\) phút
- Thời gian ca nô đi từ A đến B tính cả thời gian nghỉ = thời gian lúc ca nô đi đến bến B – thời gian lúc ca nô đi từ bến sông A.
- Thời gian ca nô đi từ A đến B không tính thời gian nghỉ = Thời gian ca nô đi từ A đến B tính cả thời gian nghỉ – thời gian nghỉ.
Tính cả thời gian nghỉ ca nô đi từ A đến B hết số thời gian là:
\(9\) giờ \(10\) phút \( - \,7\) giờ \(15\) phút \( = \,1\) giờ \(55\) phút
Nếu không tính thời gian nghỉ ca nô đi từ A đến B hết số thời gian là:
\(1\) giờ \(55\) phút \( - \,10\) phút \( = \,1\) giờ \(45\) phút
Đáp số: \(1\) giờ \(45\) phút.

Trung bình một người thợ làm xong một sản phẩm hết \(1\) giờ \(12\) phút. Lần thứ nhất người đó làm được \(6\) sản phẩm. Lần thứ hai người đó làm được \(8\) sản phẩm. Hỏi cả hai lần người đó phải làm trong bao nhiêu thời gian?
A. \(16\) giờ \(48\) phút
B. \(16\) giờ \(36\) phút
C. \(15\) giờ \(12\) phút
D. \(9\) giờ \(36\) phút
A. \(16\) giờ \(48\) phút
Cách 1:
- Tính thời gian làm \(6\) sản phẩm = thời gian làm \(1\) sản phẩm \( \times \,6\).
- Tính thời gian làm \(8\) sản phẩm = thời gian làm \(1\) sản phẩm \( \times \,8\).
- Tính thời gian làm cả hai lần = thời gian làm \(6\) sản phẩm + thời gian làm \(8\) sản phẩm.
Cách 2:
- Tìm tổng số sản phẩm làm trong hai lần \(= 6\, + 8 = 14\) sản phẩm.
- Tính thời gian làm cả hai lần = thời gian làm \(1\) sản phẩm \( \times \,14\).
Lưu ý: Nếu số phút ở kết quả lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn phút là giờ.
Cách 1:
Người đó làm \(6\) sản phẩm trong số thời gian là:
\(1\) giờ \(12\) phút \( \times \,6\, = \,6\) giờ \(72\) phút
Đổi \(\,\,6\) giờ \(72\) phút \( = \,7\) giờ \(12\) phút
Người đó làm \(8\) sản phẩm trong số thời gian là:
\(1\) giờ \(12\) phút \( \times \,8\, = \,8\) giờ \(96\) phút
Đổi \(8\) giờ \(96\) phút \( = \,9\) giờ \(36\) phút
Cả hai lần người đó phải làm trong số thời gian là:
\(\,7\) giờ \(12\) phút\( + \,9\) giờ \(36\) phút \( = \,16\) giờ \(48\) phút
Cách 2
Cả hai lần người đó làm được số sản phẩm là
\(6 + 8 = 14\) (sản phẩm)
Cả hai lần người đó phải làm trong số thời gian là:
\(1\) giờ \(12\) phút \( \times \,14\, = \,14\) giờ \(168\) phút
Đổi \(\,14\) giờ \(168\) phút \( = \,16\) giờ \(48\) phút
Đáp số: \(16\) giờ \(48\) phút.

Tính: \(12\) phút \(25\) giây \( \times \,3\, + \,\)\(27\) phút \(32\) giây \( \times \,4\)
A. \(4\) giờ \(19\) phút \(8\) giây
B.\(3\) giờ \(54\) phút \(15\) giây
C. \(2\) giờ \(18\) phút \(32\) giây
D. \(2\) giờ \(27\) phút \(23\) giây
D. \(2\) giờ \(27\) phút \(23\) giây
- Ta thực hiện tính giá trị biểu thức như đối với các số tự nhiên, tính lần lượt phép nhân trước, phép cộng sau.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
- Nếu số phút lớn hơn hoặc bằng \(60\) thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của phút là giờ; số giây lớn hơn hoặc bằng \(60\) thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của giây là phút.
Ta có:
\(12\) phút \(25\) giây \( \times \,\,\,3\,\,\, + \,\,27\) phút \(32\) giây \( \times \,\,4\)
\( = \,\,36\) phút \(75\) giây \( + \,\,108\) phút \(128\) giây
\( = \,\,37\) phút \(15\) giây \( + \,\,110\) phút \(8\) giây
\( = \,\,147\) phút \(23\) giây
\( = \,\,2\) giờ \(27\) phút \(23\) giây

Điền dấu (\(>;\,<;\,=\)) thích hợp vào ô trống:
\(2\) ngày \(9\) giờ \( \times \,3\)
\((18\) ngày \(3\) giờ \( - \,3\) ngày \(21\) giờ\() \,:\,2\)
\(2\) ngày \(9\) giờ \( \times \,3\)
\((18\) ngày \(3\) giờ \( - \,3\) ngày \(21\) giờ\() \,:\,2\)
- Tính giá trị từng vế như đối với các số tự nhiên, tính trong ngoặc trước, ngoài ngoặc sau.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng. Nếu số giây lớn hơn hoặc bằng \(60\) thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của giây là phút.
- So sánh kết quả với nhau.
Ta có:
+) \(2\) ngày \(9\) giờ \( \times \,3\, = \,6\) ngày \(27\) giờ \( = \,7\) ngày \(3\) giờ;
+) \((18\) ngày \(3\) giờ \( - \,3\) ngày \(21\) giờ \()\,\,:\,\,2\)
\( = \,\,(17\) ngày \(27\) giờ \( - \,\,3\) ngày \(21\) giờ \()\,\,:\,\,2\)
\( = \,\,14\) ngày \(6\) giờ \(\,:\,\,2\)
\( = \,\,7\) ngày \(3\) giờ
Mà \(7\) ngày \(3\) giờ \( = \,\,7\) ngày \(3\) giờ.
Do đó: \(2\) ngày \(9\) giờ \( \times \,3\, = \,(18\) ngày \(3\) giờ \( - \,3\) ngày \(21\) giờ\()\,\,:\,\,2\).

Điền số thích hợp vào ô trống:
Một ô tô đi lên dốc quãng đường AB hết \(1\) giờ \(35\) phút và đi tiếp xuống dốc trên quãng đường BC hết thời gian ít hơn thời gian lên dốc là \(0,4\) giờ.
Vậy ô tô đi cả hai quãng đường AB và BC hết
giờ
phút.
Một ô tô đi lên dốc quãng đường AB hết \(1\) giờ \(35\) phút và đi tiếp xuống dốc trên quãng đường BC hết thời gian ít hơn thời gian lên dốc là \(0,4\) giờ.
Vậy ô tô đi cả hai quãng đường AB và BC hết
giờ
phút.
- Đổi \(0,4\) giờ ra đơn vị phút ta lấy \(60\) phút nhân với \(0,4\) được \(24\) phút.
- Tính thời gian ô tô xuống dốc ta lấy thời gian ô tô đi lên dốc trừ đi \(24\) phút.
- Tính thời gian ô tô đi cả hai quãng đường ta tính tổng thời gian ô tô lên dốc và thời gian ô tô xuống dốc.
Đổi \(0,4\) giờ \( = \,24\) phút.
Ô tô đi xuống dốc trên quãng đường BC hết số thời gian là:
\(1\) giờ \(35\) phút \( - \,24\) phút \( = \,1\) giờ \(11\) phút
Ô tô đi cả hai quãng đường AB và BC hết số thời gian là:
\(1\) giờ \(35\) phút \( + \,1\) giờ \(11\) phút \( = \,2\) giờ \(46\) phút
Đáp số: \(\,2\) giờ \(46\) phút.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(2\,;\,\,46\).
.jpg)
Mai đi từ nhà lúc \(7\) giờ \(15\) phút và đến trường sớm \(8\) phút so với giờ vào học. Lan đi từ nhà lúc \(7\) giờ \(20\) phút và đến trường đúng giờ vào học. Biết giờ vào học là \(8\) giờ. Hỏi Mai và Lan, ai đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn bao nhiêu phút?
A. Mai ; \(3\) phút
B. Mai ; \(5\) phút
C. Lan ; \(3\) phút
D. Lan ; \(5\) phút
C. Lan ; \(3\) phút
- Tìm thời gian lúc Mai đi tới trường: Mai đến trường sớm \(8\) phút tức là đến trường lúc \(8\) giờ kém \(8\) phút hay \(7\) giờ \(52\) phút.
- Tính thời gian Mai đi từ nhà đến trường ta lấy thời gian lúc Mai đi tới trường trừ đi thời gian lúc Mai đi từ nhà.
- Tính thời gian Lan đi từ nhà đến trường ta lấy thời gian lúc Lan đi tới trường trừ đi thời gian lúc Lan đi từ nhà.
- So sánh hai kết quả để tìm ai đi mất nhiều thời gian hơn.
- Tìm thời gian đi nhiều hơn ta lấy số đo thời gian lớn hơn trừ đi số đo thời gian bé hơn.
Mai đến trường sớm \(8\) phút tức là đến trường lúc \(8\) giờ kém \(8\) phút hay \(7\) giờ \(52\) phút.
Thời gian Mai đi từ nhà đến trường là:
\(7\) giờ \(52\) phút \( - \,7\) giờ \(15\) phút \( = \,37\) phút
Thời gian Lan đi từ nhà đến trường là:
\(8\) giờ \( - \,7\) giờ \(20\) phút \( = \,40\) phút
Ta có: \(40\) phút \( > \,37\) phút.
Vây Lan đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn số thời gian là:
\(\,\,40\) phút \( - \,37\) phút \( = \,3\) phút
Đáp số: Lan ; \(3\) phút.

Điền số thích hợp vào ô trống:
Bác thợ mộc làm một bộ bàn ghế gồm \(1\) cái bàn và \(4\) cái ghế hết \(22\) giờ \(30\) phút.
Biết rằng thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế.
Vậy trung bình làm một cái ghế mất
giờ
phút.
Bác thợ mộc làm một bộ bàn ghế gồm \(1\) cái bàn và \(4\) cái ghế hết \(22\) giờ \(30\) phút.
Biết rằng thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế.
Vậy trung bình làm một cái ghế mất
giờ
phút.
Theo đề bài thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế nên thời gian làm \(4\) cái ghế gấp \(2\) lần thời gian làm \(1\) cái bàn.
Lại có thời gian làm \(1\) cái bàn và \(4\) cái ghế hết \(22\) giờ \(30\) phút.
Từ đó ta có bài toán dạng tìm hai số khi biết tổng và tỉ số. Ta vẽ sơ đồ biểu thị thời gian làm \(1\) cái bàn gồm \(1\) phần và thời gian làm \(4\) cái ghế gồm \(2\) phần như thế. Coi thời gian làm \(1\) cái bàn là số bé, thời gian làm \(4\) cái ghế là số lớn, ta tìm hai số theo công thức:
Số bé = Giá trị một phần × số phần của số bé
hoặc
Số lớn = Giá trị một phần × số phần của số lớn.
Theo đề bài thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế nên thời gian làm \(4\) cái ghế gấp \(2\) lần thời gian làm \(1\) cái bàn.
Ta có sơ đồ:
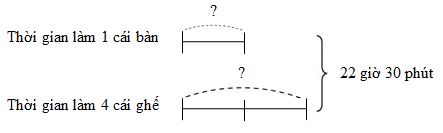
Theo sơ đồ, tổng số phần bằng nhau là:
\(1 + 2 = 3\) (phần)
Giá trị một phần hay thời gian làm \(1\) cái bàn là:
\(22\) giờ \(30\) phút \(:\,3\, = \,7\) giờ \(30\) phút
Thời gian trung bình để làm \(1\) cái ghế là:
\(\,7\) giờ \(30\) phút \(:\,2\, = \,3\) giờ \(45\) phút
Đáp số: \(3\) giờ \(45\) phút.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(3\,;\,\,45\).
