.png)
A. Khi nhân một số thập phân với \(10,{\rm{ }}100,{\rm{ }}1000,{\rm{ }}...\) ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số.
B. Khi nhân một số thập phân với \(0,1;\,\,0,01;\,\,0,001;\,\,...\) ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
C. Cả A và B đều sai
D. Cả A và B đều đúng.
D. Cả A và B đều đúng.
Dựa vào quy tắc nhân một số thập phân với \(10,{\rm{ }}100,{\rm{ }}1000,{\rm{ }}...\); với \(0,1;\,\,0,01;\,\,0,001;\,\,...\)
- Khi nhân một số thập phân với \(10,{\rm{ }}100,{\rm{ }}1000,{\rm{ }}...\) ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số.
- Khi nhân một số thập phân với \(0,1;\,\,0,01;\,\,0,001;\,\,...\) ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Vậy cả A và B đều đúng.
.jpg)
Điền số thích hợp vào ô trống:
Tính nhẩm :
\(38,04 \times 10 = \)
\(38,04 \times 10 = \)
Khi nhân một số thập phân với \(10\) ta chỉ việc chuyển dấu phẩy của số đó sang bên phải một chữ số.
Khi nhân một số thập phân với \(10\) ta chỉ việc chuyển dấu phẩy của số đó sang bên phải một chữ số.
Do đó ta có: \(38,04 \times 10 = 380,4\).
Vậy số thích hợp điền vào ô trống là \(380,4\).
.png)
Điền số thích hợp vào ô trống:
\(9,8 \times 34 = \)
\(9,8 \times 34 = \)
Đặt tính rồi tính :
- Nhân như nhân các số tự nhiên.
- Phần thập phân của số \(9,8\) có một chữ số, ta dùng dấu phẩy tách ở tích ra một chữ số kể từ phải sang trái.
Ta đặt tính và thực hiện tính như sau:
\(\begin{array}{*{20}{c}}{ \times \begin{array}{*{20}{c}}{9,\,8}\\{3\,\,4}\end{array}}\\\hline{3\,9\,2}\\{\,2\,9\,4\,\,\,\,\,\,\,\,}\\\hline{3\,33,2\,\,\,}\end{array}\,\)
Vậy đáp án đúng điền vào ô trống là \(333,2\).
.jpg)
Tính: \(31,6 \times 7,2\)
A. \(222,42\)
B. \(224,72\)
C. \(225,72\)
D. \(227,52\)
D. \(227,52\)
Đặt tính rồi tính:
- Nhân như nhân các số tự nhiên.
- Đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Ta đặt tính và thực hiện tính như sau:
\(\begin{array}{*{20}{c}}{ \times \begin{array}{*{20}{c}}{31,6}\\{\,\,7,2}\end{array}}\\\hline{\,\,\,6\,3\,2}\\{\,\,2\,2\,12\,\,\,\,\,\,\,\,\,\;}\\\hline{227,52\,\,\,\,}\end{array}\,\)
Vậy: \(31,6 \times 7,2 = 227,52\).
.png)
Điền số thích hợp vào ô trống:
Tính nhẩm: \(6798,4 \times 0,001 = \)
Tính nhẩm: \(6798,4 \times 0,001 = \)
Khi nhân một số thập phân với \(0,001\) ta chỉ việc chuyển dấu phẩy của số đó sang bên trái ba chữ số.
Khi nhân một số thập phân với \(0,001\) ta chỉ việc chuyển dấu phẩy của số đó sang bên trái ba chữ số.
Do đó ta có: \(6798,4 \times 0,001 = 6,7984\)
Vậy đáp án đúng điền vào ô trống là \(6,7984\).
.jpg)
Điền số thích hợp vào ô trống:
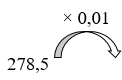
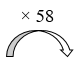


- Tính lần lượt từ trái sang phải.
- Áp dụng quy tắc nhân một số tự nhiên với một số thập phân, nhân nhẩm một số thập phân với \(0,01\).
Tính lần lượt từ trái sang phải ta có:
\(\begin{array}{l}278,5 \times 0,01 = 2,785;\\2,785 \times 58 = 161,53\end{array}\)
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(2,785\,;\,\,161,53\).
.jpg)
Tìm \(x\), biết \(x:6,2 = 52,2 + 12,4 \times 0,1\)
A. \(x = 40,052\)
B. \(x = 42,042\)
C. \(x = 331,328\)
D. \(x = 333,318\)
C. \(x = 331,328\)
- Tính giá trị vế phải: biểu thức có chứa phép nhân và phép cộng nên ta tính phép nhân trước, tính phép cộng sau.
- \(x\) ở vị trí số bị chia nên để tìm \(x\) ta lấy thương nhân với số chia.
Ta có:
\(\begin{array}{l}x:6,2 = 52,2 + 12,4 \times 0,1\\x:6,2 = 52,2 + 1,24\\x:6,2 = 53,44\\x = 53,44 \times 6,2\\x = 331,328\end{array}\)
Vậy \(x = 331,328\).
.jpg)
Điền số thích hợp vào ô trống:
\(15,756km = \)
\(m\).
\(15,756km = \)
\(m\).
Theo bảng đơn vị đo độ dài ta có \(1km = 1000m\), vậy muốn đổi từ đơn vị là ki-lô-mét sang đơn vị mét ta chỉ việc nhân với \(1000\).
Ta có \(1km=1000m\) và \(15,756 \times 1000 = 15756\).
Do đó: \(15,756km = 15756m\).
Vậy đáp án đúng điền vào ô trống là \(15756\).
.jpg)
Điền dấu (\(>;<;=\)) thích hợp vào ô trống:
\(654 - 4,85 \times 68 + 506,1\)
\(38,3 \times 24 - 254 \times 0,35\)
\(654 - 4,85 \times 68 + 506,1\)
\(38,3 \times 24 - 254 \times 0,35\)
- Tính giá trị hai vế: biểu thức có chứa phép nhân, phép cộng, phép trừ nên ta tính phép nhân trước, phép cộng, phép trừ sau. Khi biểu thức chỉ chứa phép cộng và phép trừ, ta tính lần lượt từ trái sang phải.
- So sánh hai kết quả vừa tìm được.
Ta có:
\(\begin{array}{l}654 - 4,85 \times 68 + 506,1 & & & 38,3 \times 24 - 254 \times 0,35\\ = 654 - 329,8 + 506,1 & & & = 919,2 - 88,9\\ = 324,2 + 506,1 & & & = 830,3\\ = 830,3\end{array}\)
Mà \(830,3 = 830,3\)
Do đó: \(654 - 4,85 \times 68 + 506,1 = 38,3 \times 24 - 254 \times 0,35 \)
Vậy dấu thích hợp điền vào ô trống là \( = \).

Điền số thích hợp vào ô trống để tính bằng cách thuận tiện :
\(45,54 \times 26 + 45,54 + 45,54 \times 73\)
\( = 45,54 \times 26 + 45,54 \times \)
\( + \,45,54 \times 73\)
\( = \)
\( \times \,\,\,(\,26\) +
\(+ 73 ) \)
\( = \)
\(\times (\)
\(+ 73 )\)
\(=\)
\(\times\)
\(=\)
\(45,54 \times 26 + 45,54 + 45,54 \times 73\)
\( = 45,54 \times 26 + 45,54 \times \)
\( + \,45,54 \times 73\)
\( = \)
\( \times \,\,\,(\,26\) +
\(+ 73 ) \)
\( = \)
\(\times (\)
\(+ 73 )\)
\(=\)
\(\times\)
\(=\)
Áp dụng công thức \(a \times b + a + a \times c = a \times b + a \times 1 + a \times c = a \times (b + 1 + c)\)
\(\begin{array}{l}45,54 \times 26 + 45,54 + 45,54 \times 73\\ = 45,54 \times 26 + 45,54 \times 1 + 45,54 \times 73\\ = 45,54 \times (26 + 1 + 73)\\ = 45,54 \times 100\\ = 4554\end{array}\)
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là \(1\,;\,\,45,54\,;\,\,1\,;\,\,45,54\,;\,\,27\,;\,\,45,54\,;\,\,100\,;\,\,4554\).
.jpg)
Điền số thích hợp vào ô trống:
Một túi kẹo nặng \(0,35kg\) và một túi bánh nặng \(0,75kg\).
Vậy \(12\) túi kẹo và \(25\) túi bánh như thế nặng tất cả
\(kg\).
Một túi kẹo nặng \(0,35kg\) và một túi bánh nặng \(0,75kg\).
Vậy \(12\) túi kẹo và \(25\) túi bánh như thế nặng tất cả
\(kg\).
- Tính cân nặng của \(12\) túi kẹo ta lấy cân nặng của một túi nhân với \(12\).
- Tính cân nặng của \(25\) túi bánh ta lấy cân nặng của một túi nhân với \(25\).
- Tính cân nặng \(12\) túi kẹo và \(25\) túi bánh ta lấy cân nặng của \(12\) túi kẹo cộng với cân nặng của \(25\) túi bánh.
\(12\) túi kẹo nặng số ki-lô-gam là:
\(0,35 \times 12 = 4,2\;(kg)\)
\(25\) túi bánh nặng số ki-lô-gam là:
\(0,75 \times 25 = 18,75\;(kg)\)
\(12\) túi kẹo và \(25\) túi bánh nặng tất cả số ki-lô-gam là:
\(4,2 + 18,75 = 22,95\;(kg)\)
Đáp số: \(22,95kg\).
Vậy đáp án đúng điền vào ô trống là \(22,95\).

Một can nhựa chứa \(100\) lít dầu hỏa. Biết một lít dầu hỏa cân nặng \(0,8kg\), can rỗng cân nặng \(12,5kg\). Hỏi can dầu hỏa đó cân nặng bao nhiêu ki-lô-gam?
A. \(67,5kg\)
B. \(80kg\)
C. \(92,5kg\)
D. \(133kg\)
C. \(92,5kg\)
- Tính cân nặng của \(100\) lít dầu hỏa ta lấy cân nặng của một lít dầu hỏa nhân với \(100\).
- Tính cân nặng của can dầu hỏa ta lấy cân nặng của \(100\) lít dầu hỏa cộng với cân nặng can rỗng.
\(100\) lít dầu hỏa nặng số ki-lô-gam là:
\(0,8 \times 100 = 80 \;(kg)\)
Can dầu hỏa đó nặng số ki-lô-gam là:
\(80 + 12,5 = 92,5\;(kg)\)
Đáp số: \(92,5kg\).
.jpg)
Tìm một số thập phân biết rằng khi chia số đó cho \(3,25\) rồi cộng với \(24,56\) thì được kết quả là một số tự nhiên lớn nhất có hai chữ số.
A. \(401,57\)
B. \(238,68\)
C. \(2747,25\)
D. \(241,93\)
D. \(241,93\)
Số tự nhiên lớn nhất có hai chữ số là \(99\).
Giả xử \(x\) là số thập phân cần tìm. Theo đề bài ta có \(x:3,25 + 24,56 = 99\). Từ đó ta tìm được \(x\).
Số tự nhiên lớn nhất có hai chữ số là \(99\).
Giả xử \(x\) là số thập phân cần tìm. Theo đề bài ta có \(x:3,25 + 24,56 = 99\).
\(\begin{array}{l}x:3,25 + 24,56 = 99\\x:3,25 = 99 - 24,56\\x:3,25 = 74,44\\x = 74,44 \times 3,25\\x = 241,93\end{array}\)
Vậy số thập phân cần tìm là \(241,93\).

Điền số thích hợp vào ô trống:
Cho hình H có số đo như hình vẽ. Biết hình H bao gồm hình chữ nhật ABCD và hình vuông MNPC.
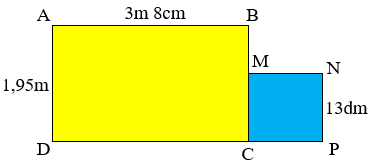
Vậy diện tích của hình H là
\(m^2\).
Cho hình H có số đo như hình vẽ. Biết hình H bao gồm hình chữ nhật ABCD và hình vuông MNPC.

Vậy diện tích của hình H là
\(m^2\).
- Đưa độ dài các cạnh về cùng đơn vị đo là mét.
- Tính diện tích hình chữ nhật ABCD theo công thức: Diện tích = chiều dài × chiều rộng.
- Tính diện tích hình vuông MNPC theo công thức: Diện tích = độ dài cạnh × độ dài cạnh .
- Tính diện tích hình H = Diện tích hình chữ nhật ABCD + Diện tích hình vuông MNPC.
Đổi \(13dm = 1,3m;\,\,\,\,\,\,3m\,8cm = 3,08m\)
Diện tích hình chữ nhật ABCD là:
\(3,08 \times 1,95 = 6,006({m^2})\)
Diện tích hình vuông MNPC là:
\(1,3 \times 1,3 = 1,69({m^2})\)
Diện tích hình H là:
\(6,006 + 1,69 = 7,696({m^2})\)
Đáp số: \(7,696{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(7,696\).

Điểm kiểm tra trung bình của lớp 5A là \(8,02\) điểm và điểm trung bình của học sinh nữ là \(8,07\) điểm. Biết lớp 5A có 28 học sinh, số học sinh nam nhiều hơn số học sinh nữ là \(4\) học sinh. Tính tổng số điểm của học sinh nam đạt được.
A. \(224,56\) điểm
B. \(127,72\) điểm
C. \(128,32\) điểm
D. \(96,84\) điểm
B. \(127,72\) điểm
- Tìm số học sinh nam và học sinh nữ của lớp dựa vào bài toán tổng – hiệu: lớp 5A có 28 học sinh, số học sinh nam nhiều hơn số học sinh nữ là \(4\) học sinh:
Số lớn = (tổng + hiệu) \(:{\rm{ }}2\) ; số bé = (tổng – hiệu) \(:{\rm{ }}2\)
- Tìm tổng số điểm cả lớp đạt được và tổng số điểm học sinh nữ đạt được theo công thức: Tổng = trung bình cộng × số số hạng.
- Tìm tổng số điểm của học sinh nam đạt được ta lấy tổng số điểm cả lớp đạt được trừ đi tổng số điểm của học sinh nữ đạt được.
Lớp 5A có số học sinh nam là:
\((28 + 4):2 = 16\) (học sinh)
Lớp 5A có số học sinh nữ là:
\(28 - 16 = 12\) (học sinh)
Tổng số điểm của cả lớp đạt được là:
\(8,02 \times 28 = 224,56\) (điểm)
Tổng số điểm của học sinh nữ đạt được là:
\(8,07 \times 12 = 96,84\) (điểm)
Tổng số điểm của học sinh nam đạt được là:
\(224,56 - 96,84 = 127,72\) (điểm)
Đáp số: \(127,72\) điểm.
