
Phép cộng số thập phân có những tính chất nào dưới đây?
A. Tính chất giao hoán
B. Tính chất kết hợp
C. Tính chất cộng với \(0\)
D. Cả A, B, C đều đúng
D. Cả A, B, C đều đúng
Phép cộng số thập phân có đầy đủ các tính chất như phép cộng số tự nhiên.
Phép cộng số thập phân có các tính chất:
+) Tính chất giao hoán: Khi đổi chỗ hai số hạng trongg một tổng thì tổng không thay đổi.
+) Tính chất kết hợp: Khi cộng một tổng hai số với số thứ ba thì ta có thể cộng số thứ nhất với tổng của hai số còn lại.
+) Cộng với số \(0\): Số thập phân nào cộng với \(0\) cũng bằng chính số thập phân đó.
Vậy cả A, B, C đều đúng.
.png)
Cho phép tính : \(18,253 + 7,7\). Cách đặt tính nào sau đây là đúng?
A. $\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{1\,8\,,\,2\,5\,3}\\{\,\,\,\,\,\,\,\,\,\,\,\,\,7,7}\end{array}}\\\hline{}\end{array}$
B. $\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{\,\,\, 1\,\,8\,,\,2\,5\,3}\\{7,7\,\,\,\,\,\,\,\,\,}\end{array}}\\\hline{}\end{array}$
C. $\begin{array}{*{20}{c}}{ + \,\,\begin{array}{*{20}{c}}{1\,\,8\,,\,2\,5\,3}\\{\,\,\,7,7\,\,\,\,\,\,\,}\end{array}}\\\hline{}\end{array}$
D. $\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{1\,8\,,\,2\,5\,3}\\{\,\,\,\,\,\,\, 7,7}\end{array}}\\\hline{}\end{array}$
C. $\begin{array}{*{20}{c}}{ + \,\,\begin{array}{*{20}{c}}{1\,\,8\,,\,2\,5\,3}\\{\,\,\,7,7\,\,\,\,\,\,\,}\end{array}}\\\hline{}\end{array}$
Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau, các dấu phẩy của các số hạng thẳng cột với nhau.
Khi đặt tính, ta viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau, các dấu phẩy của các số hạng thẳng cột với nhau.
Vậy trong các cách đặt tính chỉ có cách đặt C là đúng.
.png) Thực hiện tính: \( 17,36+42,52 = ?\)
Thực hiện tính: \( 17,36+42,52 = ?\)
A. \( 58,98\)
B. \(59,88\)
C. \( 4269,36\)
D. \(5988 \)
B. \(59,88\)
Muốn cộng hai số thập phân ta làm như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Cộng như cộng các số tự nhiên.
- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.
Ta đặt tính và thực hiện tính như sau:
$\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{\,17,36}\\{\,42,52}\end{array}}\\\hline{\,\,\,\,\,\,59,88}\end{array}$
Vậy \(17,36 + 42,52 = 59,88 \).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
\(83,7+9,68 =\)
\(83,7+9,68 =\)
Muốn cộng hai số thập phân ta làm như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Cộng như cộng các số tự nhiên.
- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.
Ta đặt tính và đặt tính như sau:
$\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{83,7\,\,}\\{\,\,\,9,68}\end{array}}\\\hline{\,\,\,\,93,38}\end{array}$
Vậy \(83,7 + 9,68 = 93,38\).

Tính: \(5,3 + 38,93 + 16\)
A. \(44,39\)
B. \(55,46\)
C. \(60,23\)
D. \(107,93\)
C. \(60,23\)
Để tính tổng nhiều số thập phân ta làm tương tự như tính tổng hai số thập phân.
Ta đặt tính và thực hiện tính như sau:
$\begin{array}{*{20}{c}}{ + \,\,\begin{array}{*{20}{c}}{5,3}\\\begin{array}{l}38,93\\16\end{array}\end{array}}\\\hline{\,\,\,\,\,\,60,23}\end{array}$
Vậy \(5,3+38,93+16=60,23\).

Tìm \(x\) biết: \(x - 4,5 = 7,98\)
A. \(x = 52,98\)
B. \(x = 84,3\)
C. \(x = 8,43\)
D. \(x = 12,48\)
D. \(x = 12,48\)
\(x\) ở vị trí là số bị trừ, muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
Ta có:
\(\begin{array}{l}x - 4,5 = 7,98\\x = 7,98 + 4,5\\x = 12,48\end{array}\)
Vậy \(x = 12,48\).
 Điền dấu \((>,\, <, \, =)\) thích hợp vào ô trống:
Điền dấu \((>,\, <, \, =)\) thích hợp vào ô trống:
\(4,8 + 9,5\)
\(13,4\)
\(4,8 + 9,5\)
\(13,4\)
Tính giá trị ở vế trái rồi so sánh hai số thập phân.
Ta có : \(4,8 + 9,5\,= \,14,3\,\).
Mà \(14,3 \, > \,13,4\).
Vậy \(4,8 + 9,5\,\, > \,\,13,4\).
 Kéo thả dấu thích hợp vào ô trống:
Kéo thả dấu thích hợp vào ô trống:
Sử dụng tính chất giao hoán của phép cộng số thập phân.
Vì phép cộng các số thập phân có tính chất giao hoán nên khi đổi chỗ hai số hạng trong một tổng thì tổng không thay đổi.
Do đó: \(27,3 + 15,6\, = \,15,6 + 27,3\).
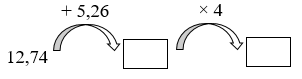
Số thích hợp điền vào ô trổng lần lượt từ trái sang phải là:
A. \(17\) và \(68\)
B. \(18\) và \(72\)
C. \(19\) và \(76\)
B. \(18\) và \(72\)
Ta tính lần lượt tự trái sang phải.
Tính theo thứ tự từ trái sang phải ta được:
\(\begin{array}{l}12,74 + 5,26 = 18\\18 \times 4 = 72\end{array}\).
Vậy các số cần điền vào ô trống lần lượt từ trái sang phải là \(18\,;\,\,72\).

Điền số thích hợp vào ô trống:
Tính bằng cách thuận tiện nhất:
\(38,64 + 123,52 + 61,36 + 231,48\)
\( = (38,64 +\)
\( ) \,+ \,(123,52 + \)
\( )\)
\( = \)
\( + \)
\( = \)
Tính bằng cách thuận tiện nhất:
\(38,64 + 123,52 + 61,36 + 231,48\)
\( = (38,64 +\)
\( ) \,+ \,(123,52 + \)
\( )\)
\( = \)
\( + \)
\( = \)
Nhóm các số thập phân có phần thập phân cộng với nhau thành các số tròn chục, tròn trăm, tròn nghìn, ...
Áp dụng tính chất giao hoán và kết hợp của phép cộng các số thập phân ta có:
\(\begin{array}{l}38,64 + 123,52 + 61,36 + 231,48\\ = (38,64 + 61,36) + (123,52 + 231,48)\\ = 100 + 355\\ = 455\end{array}\)
Vậy số thích hợp điền vào ô trống từ trái sang phải, từ trên xuống dưới lần lượt là \(61,36\,;\,\, 231,48\,;\,\, 100\,;\,\,355\,; \,\, 455\).

Điền số thích hợp vào ô trống:
Lan cao \(1,48m\). Minh cao hơn Lan \(0,25m\). Vậy Minh cao
\(m\).
Lan cao \(1,48m\). Minh cao hơn Lan \(0,25m\). Vậy Minh cao
\(m\).
Minh cao hơn Lan \(0,25m\) nên để tính chiều cao của Minh ta lấy chiều cao của Lan cộng với \(0,25m\).
Minh cao số mét là:
\(1,48 + 0,25 = 1,73(m)\)
Đáp số: \(1,73m\).
Vậy số thích hợp điền vào ô trống là \(1,73\).
Kéo thả số thích hợp điền vào ô trống:
- Mảnh vải xanh dài hơn mảnh vải đỏ \(12,8m\) nên để tính độ dài mảnh vải xanh ta lấy độ dài mảnh vải đỏ cộng với \(12,8m\).
- Tính độ dài cả hai mảnh ta lấy độ dài mảnh vải đỏ cộng độ dài mảnh vải xanh.
Mảnh vải xanh dài số mét là:
\(57,45 + 12,8 = 70,25(m)\)
Cả hai mảnh vải dài số mét là:
\(57,45 + 70,25 = 127,7(m)\)
Đáp số: \(127,7m\).
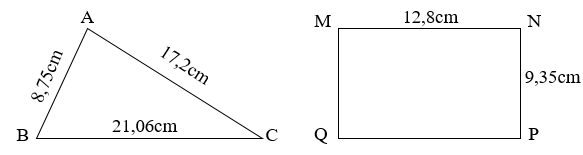
Cho tam giác ABC và hình chữ nhật MNPQ có kích thước như hình vẽ. Hỏi hình nào có chu vi lớn hơn?
A. Hình tam giác ABC
B. Hình chữ nhật MNPQ
C. Hai hình có chu vi bằng nhau
A. Hình tam giác ABC
- MNPQ là hình chữ nhật nên MN = PQ = \(12,8cm\); NP = MQ = \(9,35cm\).
- Tính chu vi của hai hình rồi so sánh:
+) Chu vi hình tam giác bằng tổng độ dài ba cạnh AB, BC, AC.
+) Chu vi hình chữ nhật MNPQ bằng tổng độ dài bốn cạnh MN, NP, PQ, MQ.
Vì MNPQ là hình chữ nhật nên MN = PQ = \(12,8cm\); NP = MQ = \(9,35cm\).
Chu vi hình chữ nhật MNPQ là:
\(12,8 + 9,35 + 12,8 + 9,35 = 44,3\;(cm)\)
Chu vi tam giác ABC là:
\(8,75 + 21,06 + 17,2 = 47,01\;(cm)\)
Ta có \(47,01 > 44,3\) nên \(47,01cm > 44,3cm\).
Vậy tam giác ABC có chu vi lớn hơn.

Điền số thích hợp vào ô trống:
Có ba thùng đựng dầu, thùng thứ nhất có \(36,5\,\) lít dầu, thùng thứ hai có nhiều hơn thùng thứ nhất \(8,2\) lít dầu nhưng ít hơn thùng thứ ba \(3,57\,\) lít dầu.
Vậy ba thùng có tất cả
lít dầu.
Có ba thùng đựng dầu, thùng thứ nhất có \(36,5\,\) lít dầu, thùng thứ hai có nhiều hơn thùng thứ nhất \(8,2\) lít dầu nhưng ít hơn thùng thứ ba \(3,57\,\) lít dầu.
Vậy ba thùng có tất cả
lít dầu.
- Thùng thứ hai có nhiều hơn thùng thứ nhất \(8,2\) lít dầu nên để tính số dầu thùng thứ hai ta lấy số dầu thùng thứ nhất cộng với \(8,2\) lít.
- Thùng thứ hai có ít hơn thùng thứ ba \(3,57\,\) lít dầu tức là thùng thứ ba có nhiều hơn thùng thứ hai \(3,57\,\) lít dầu. Để tính số dầu thùng thứ ba ta lấy số dầu thùng thứ hai cộng với \(3,57\) lít.
- Để tìm số dầu của cả ba thùng ta lấy số dầu của mỗi thùng cộng lại với nhau.
Thùng thứ hai có số lít dầu là
\(36,5\, + 8,2 = 44,7\) (lít)
Thùng thứ ba có số lít dầu là
\(44,7 + 3,57 = 48,27\) (lít)
Cả ba thùng có số lít dầu là
\(36,5\, + 44,7 + 48,27 = 129,47\) (lít)
Đáp số: \(129,47\) lít.
