Đề bài
Bài 1. Đúng ghi Đ, sai ghi S vào ô trống :
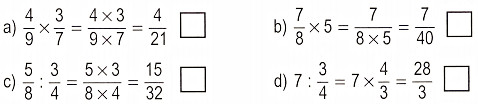
Bài 2. Tính:
a) \(\dfrac{3}{5} \times \dfrac{1}{2}\) b) \(\dfrac{3}{8} \times \dfrac{4}{7}\)
c) \(\dfrac{7}{{12}}:\dfrac{1}{4}\) d) \(15:\dfrac{5}{7}\)
Bài 3. Tìm \(x\) , biết:
\(a)\,\,x \times \dfrac{3}{8} = \dfrac{5}{6}\) \(b)\,\,x:\dfrac{4}{5} = \dfrac{{15}}{{16}}\)
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 4. Tính bằng hai cách
\(a)\,\,\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right) \times \dfrac{3}{4}\) \(b)\,\,\left( {\dfrac{7}{9} + \dfrac{2}{3}} \right):\dfrac{5}{6}\)
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 5. Một hình chữ nhật có chiều rộng là \(\dfrac{4}{5}m\), chiều dài hơn chiều rộng \(\dfrac{1}{2}m\). Tính chu vi và diện tích của hình chữ nhật đó.
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Lời giải chi tiết
Bài 1.
Phương pháp:
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Cách giải:
Ta có:
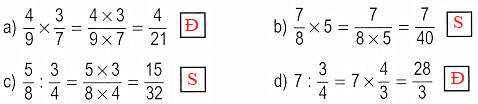
a) \(\dfrac{4}{9} \times \dfrac{3}{7} = \dfrac{{4 \times 3}}{{9 \times 7}} = \dfrac{{12}}{{63}} = \dfrac{4}{{21}};\)
b) \(\dfrac{7}{8} \times 5 = \dfrac{{7 \times 5}}{8} = \dfrac{{35}}{8};\)
c) \(\dfrac{5}{8}:\dfrac{3}{4} = \dfrac{5}{8} \times \dfrac{4}{3} = \dfrac{{5 \times 4}}{{8 \times 3}}\)\( = \dfrac{{20}}{{24}} = \dfrac{5}{6};\)
d) \(7:\dfrac{3}{4} = 7 \times \dfrac{4}{3} = \dfrac{{7 \times 4}}{3} = \dfrac{{28}}{3}.\)
Vậy ta có kết quả như sau:
Bài 2.
Phương pháp:
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Cách giải:
a) \(\dfrac{3}{5} \times \dfrac{1}{2} = \dfrac{{3 \times 1}}{{5 \times 2}} = \dfrac{3}{{10}};\)
b) \(\dfrac{3}{8} \times \dfrac{4}{7} = \dfrac{{12}}{{56}} = \dfrac{3}{{14}};\)
c) \(\dfrac{7}{{12}}:\dfrac{1}{4} = \dfrac{7}{{12}} \times \dfrac{4}{1} = \dfrac{{28}}{{12}} = \dfrac{7}{3};\)
d) \(15:\dfrac{5}{7} = 15 \times \dfrac{7}{5} = \dfrac{{15 \times 7}}{5}\)\( = \dfrac{{105}}{5} = 21.\)
Bài 3.
Phương pháp:
Áp dụng các quy tắc:
- Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
- Muốn tìm số bị chia ta lấy thương nhân với số chia.
Cách giải:
\(\begin{array}{l}a)\,\,x \times \dfrac{3}{8} = \dfrac{5}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{5}{6}:\dfrac{3}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{20}}{9}\end{array}\) \(\begin{array}{l}b)\,\,x:\dfrac{4}{5} = \dfrac{{15}}{{16}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{15}}{{16}} \times \dfrac{4}{5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{3}{4}\end{array}\)
Bài 4.
Phương pháp:
Cách 1: Áp dụng tính giá trị biểu thức có dấu ngoặc: Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
Cách 2: Khi nhân một tổng với một số ta có thể lấy từng số hạng của tổng nhân với số đó, rồi cộng các kết quả lại với nhau.
\((a + b) \times c = a \times c + b \times c\)
Cách giải:
\(a)\,\,\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right) \times \dfrac{3}{4}\)
Cách 1:
\(\begin{array}{l}\,\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right) \times \dfrac{3}{4}\\ = \dfrac{{11}}{{15}} \times \dfrac{3}{4}\\ = \dfrac{{11}}{{20}}\end{array}\)
Cách 2:
\(\begin{array}{l}\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right) \times \dfrac{3}{4}\\ = \dfrac{1}{3} \times \dfrac{3}{4} + \dfrac{2}{5} \times \dfrac{3}{4}\\ = \dfrac{1}{4} + \dfrac{3}{{10}}\\ = \dfrac{{11}}{{20}}\end{array}\)
\(b)\,\,\left( {\dfrac{7}{9} + \dfrac{2}{3}} \right):\dfrac{5}{6}\)
Cách 1:
\(\begin{array}{l}\left( {\dfrac{7}{9} + \dfrac{2}{3}} \right):\dfrac{5}{6}\\ = \dfrac{{13}}{9}:\dfrac{5}{6}\\ = \dfrac{{13}}{9} \times \dfrac{6}{5}\\ = \dfrac{{26}}{{15}}\end{array}\)
Cách 2:
\(\begin{array}{l}\left( {\dfrac{7}{9} + \dfrac{2}{3}} \right):\dfrac{5}{6}\\ = \dfrac{7}{9}:\dfrac{5}{6} + \dfrac{2}{3}:\dfrac{5}{6}\\ = \dfrac{7}{9} \times \dfrac{6}{5} + \dfrac{2}{3} \times \dfrac{6}{5}\\ = \dfrac{{14}}{{15}} + \dfrac{4}{5}\\ = \dfrac{{26}}{{15}}\end{array}\)
Bài 5.
Phương pháp:
- Tính chiều dài ta lấy chiều rộng cộng với \(\dfrac{1}{2}m\).
- Tính chu vi hình chữ nhật ta lấy chiều dài cộng với chiều rộng (cùng một đơn vị đo) rồi nhân với 2.
- Tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng (cùng một đơn vị đo).
Cách giải:
Chiều dài hình chữ nhật đó là:
\(\dfrac{4}{5} + \dfrac{1}{2} = \dfrac{{13}}{{10}}\,\,\left( m \right)\)
Chu vi hình chữ nhật đó là:
\(\left( {\dfrac{4}{5} + \dfrac{{13}}{{10}}} \right) = \dfrac{{21}}{5}\,\,\left( m \right)\)
Diện tích hình chữ nhật đó là:
\(\dfrac{{13}}{{10}} \times \dfrac{4}{5} = \dfrac{{26}}{{25}}\,\,\left( {{m^2}} \right)\)
Đáp số: Chu vi: \(\dfrac{{21}}{5}m\,\,;\)
Diện tích: \(\dfrac{{26}}{{25}}{m^2}.\)
soanvan.me
