Đề bài
Cho tam giác \(ABC\) và đường trung tuyến \(AM\). Chứng minh rằng:
\({S_{AMB}} = {S_{AMC}}\)
Phương pháp giải - Xem chi tiết
- Dựng \(AH\) là đường cao của \(\Delta ABC\).
- Áp dụng công thức tính diện tích tam giác.
Diện tích tam giác bằng nửa tích cạnh đáy và chiều cao tương ứng.
Lời giải chi tiết
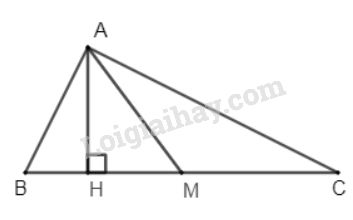
Kẻ \(AH\bot BC\). Theo công thức tính diện tích tam giác, ta có
\({S_{AMB}} = \dfrac{1}{2}BM.AH\) (1)
\({S_{AMC}} = \dfrac{1}{2}CM.AH\) (2)
Theo giả thiết \(BM = CM\) (3)
Từ (1), (2), (3) suy ra \({S_{AMB}} = {S_{AMC}}.\)
Lưu ý. Ta có nhận xét: Nếu hai tam giác có một cạnh bằng nhau và chiều cao tương ứng bằng nhau thì có diện tích bằng nhau.
soanvan.me
