Đề bài
Tính diện tích tam giác cân có cạnh đáy bằng \(a\) và cạnh bên bằng \(b.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Tam giác cân là tam giác có hai cạnh bằng nhau.
- Định lí Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng cách bình phương của hai cạnh góc vuông.
- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
Lời giải chi tiết
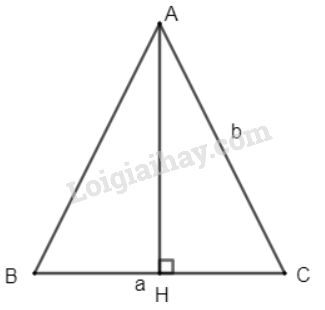
Xét \(\Delta ABC\) cân tại \(A\) có \(BC=a, AC=b\).
Kẻ \(AH\bot BC\), ta có \(BH=HC=\dfrac{a}{2}\)
Áp dụng định lý Pytago vào tam giác vuông \(ABH\), ta có
\(A{H^2} ={b^2} - {\left( {\dfrac{a}{2}} \right)^2}\), suy ra \(AH = \dfrac{{\sqrt {4{b^2} - {a^2}} }}{2}\)
Vậy \(S_{ABC} = \dfrac{1}{2}BC.AH = \dfrac{1}{2}a.\dfrac{{\sqrt {4{b^2} - {a^2}} }}{2} \)\(\,= \dfrac{1}{4}a\sqrt {4{b^2} - {a^2}} .\)
soanvan.me
