Câu 7.
Một tam giác có độ dài một cạnh tăng gấp đôi, chiều cao tương ứng không đổi. Diện tích tam giác đó tăng gấp
(A) \(8\) lần (B) \(4\) lần
(C) \(2\) lần (D) \(1,5\) lần
Phương pháp giải:
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$$S = {1 \over 2}ah$$
(\(S\) là diện tích, \(a\) là cạnh tam giác, \(h\) là chiều cao tương ứng với cạnh \(a\))
Giải chi tiết:
Gọi độ dài cạnh và chiều cao tương ứng của tam giác ban đầu là \(a;h\)
Diện tích tam giác lúc đầu là: \(S = \dfrac{1}{2}ah\)
Độ dài cạnh tăng lên gấp đôi là \(2a\)
Diện tích tam giác sau khi thay đổi là \(S' = \dfrac{1}{2}(2a).h = ah = 2S\)
Chọn C.
Câu 8.
Một tam giác cân có cạnh đáy bằng \(30\,cm\), chiều cao tương ứng bằng \(20\,cm\). Chiều cao ứng với cạnh bên bằng
(A) \(12\,cm\) (B) \(24\,cm\)
(C) \(48\,cm\) (D) Một đáp số khác.
Phương pháp giải:
- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$$S = {1 \over 2}ah$$
(\(S\) là diện tích, \(a\) là cạnh tam giác, \(h\) là chiều cao tương ứng với cạnh \(a\))
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Giải chi tiết:
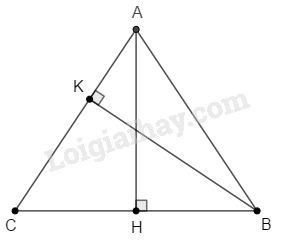
Xét tam giác \(ABC\) cân tại \(A\); \(CB=30cm;AH=20cm\)
Ta có: \(HB=CB:2=30:2=15cm\)
Áp dụng định lí Pytago vào \(\Delta AHB\) vuông tại \(H\) ta có:
\(\eqalign{
& A{B^2} = A{H^2} + H{B^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {20^2} + {15^2} = 625 = {25^2} \cr
& \Rightarrow AB = 25 ;\; AC= 25\cr} \)
\(\eqalign{
& {S_{ABC}} = {1 \over 2}AH.BC = {1 \over 2}BK.AC \cr
& \Rightarrow AH.BC = BK.AC \cr
& \Rightarrow BK = {{AH.BC} \over {AC}} = {{20.30} \over {25}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;= 24\,\left( {cm} \right) \cr} \)
Chọn B.
Câu 9.
Một tam giác đều có chiều cao bằng \(\sqrt 3 dm\). Diện tích tam giác đều đó bằng:
(A) \(3\,dm^2\)
(B) \(2\sqrt 3 \,\,d{m^2}\)
(C) \(\dfrac{{3\sqrt 3 }}{4}\,d{m^2}\)
(D) \(\sqrt 3 \,d{m^2}\)
Phương pháp giải:
- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$$S = {1 \over 2}ah$$
(\(S\) là diện tích, \(a\) là cạnh tam giác, \(h\) là chiều cao tương ứng với cạnh \(a\))
- Định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.
Giải chi tiết:
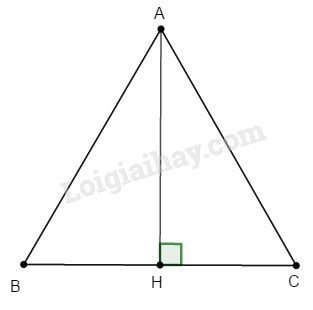
Xét tam giác \(ABC\) đều cạnh \(a\;(a>0)\), chiều cao \(AH=\sqrt 3 dm\).
Áp dụng định lí Pytago vào tam giác \(AHC\) vuông tại \(H\) ta có:
\(\eqalign{
& A{C^2} = A{H^2} + H{C^2} \cr
& {a^2} = {\left( {\sqrt 3 } \right)^2} + {\left( {{a \over 2}} \right)^2} \cr
& {a^2} = 3 + {{{a^2}} \over 4} \cr
& {a^2} - {{{a^2}} \over 4} = 3 \cr
& {{3{a^2}} \over 4} = 3 \cr
& \Rightarrow {a^2} = 3.4:3 = 4 \cr
& \Rightarrow a = 2 \cr} \)
\({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.\sqrt 3 .2 \)\(\,= \sqrt 3 \,\left( {d{m^2}} \right)\)
Chọn D.
soanvan.me
