Đề bài
Vẽ hình chữ nhật có một cạnh bằng một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.
Phương pháp giải - Xem chi tiết
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
Lời giải chi tiết
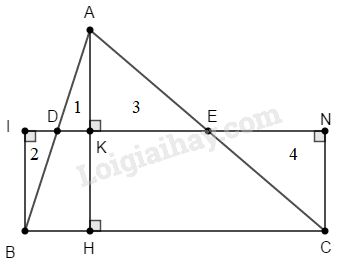
Xét \(∆ABC\) có \(BC\) là cạnh lớn nhất. Ta dựng hình chữ nhật có một cạnh bằng \(BC\) và có diện tích bằng diện tích của tam giác \(ABC\) như sau:
- Gọi \(D\) là trung điểm của \(AB\), gọi \(E\) là trung điểm của \(AC.\)
- Qua \(B\) dựng \(BI\bot DE\)
- Qua \(C\) dựng \(CN\bot DE\)
Tứ giác \(BICN\) là hình chữ nhật phải dựng.
Chứng minh: Kẻ \(AH\bot BC\) cắt \(DE\) ở \(K\).
Tứ giác \(BINC\) là hình chữ nhật vì \(\widehat B = \widehat I = \widehat N = \widehat C = {90^o}\)
\(\Delta AKD = \Delta BID\) (cạnh huyền - góc nhọn) nên \(S_1=S_2\)
\(\Delta AKE = \Delta CNE\) (cạnh huyền - góc nhọn) nên \(S_3=S_4\)
Do đó \({S_{ABC}} = {S_{BDEC}} + {S_1} + {S_3} \)\(\,= {S_{BDEC}} + {S_2} + {S_4} = {S_{BINC}}\), tức là diện tích tam giác \(ABC\) bằng diện tích hình chữ nhật.
Ta có \({S_{BINC}} = BC.BI = BC.AK \)\(\,= BC.\dfrac{1}{2}AH = \dfrac{1}{2}BC.AH\)
Kết quả trên cho ta một cách khác để chứng minh công thức diện tích tam giác.
soanvan.me
