Đề bài
Cho tam giác \(ABC\). Hãy chỉ ra một số vị trí của điểm \(M\) nằm trong tam giác đó sao cho:
\({S_{AMB}} + {S_{BMC}} = {S_{MAC}}\)
Phương pháp giải - Xem chi tiết
- Kẻ đường cao \(BH, MK.\)
- Áp dụng công thức tính diện tích tam giác: Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
Lời giải chi tiết
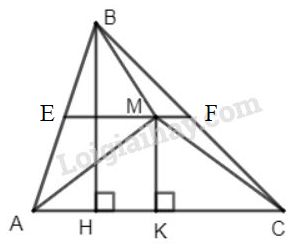
Giả sử \(M\) là điểm nằm trong tam giác \(ABC\) sao cho \({S_{AMB}} + {\rm{ }}{S_{BMC}} = {\rm{ }}{S_{MAC}}\).
Tổng diện tích của ba tam giác trên bằng \(S_{ABC}\) nên \({S_{MAC}} = \dfrac{1}{2}{S_{ABC}}\)
Hai tam giác \(MAC\) và \(ABC\) có chung đáy \(AC\).
Kẻ \(MK\bot AC, BH\bot AC.\)
Do \({S_{MAC}} = \dfrac{1}{2}{S_{ABC}}\) nên \(MK = \dfrac{1}{2}BH\)
Do đó điểm \(M\) nằm trên đường thẳng song song với \(AC\) và cách \(AC\) một khoảng bằng \(\dfrac{1}{2}BH\). Vì \(M\) nằm trong \(\Delta ABC\) nên \(M\) nằm giữa \(E\) và \(F\) (\(E\) là trung điểm \(AB\), \(F\) là trung điểm \(BC\)).
soanvan.me
