Đề bài
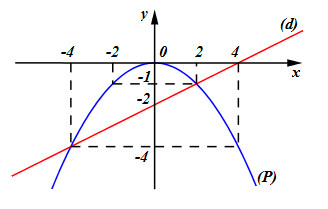
a) Vẽ parabol (P): \(y = - \dfrac{1}{4}{x^2}\) và đường thẳng (d) \(y = \dfrac{1}{2}x - 2\) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm giữa (P) và (d).
Phương pháp giải - Xem chi tiết
a) Lập bảng giá trị và vẽ đồ thị hàm số \(y = - \dfrac{1}{4}{x^2}\) và vẽ đường thẳng (d).
b) Giải phương trình hoành độ giao điểm.
Lời giải chi tiết
a) Vẽ đồ thị hàm số \(y = - \dfrac{1}{4}{x^2}\).
Bảng giá trị
|
\(x\) |
-4 |
-2 |
0 |
2 |
4 |
|
\(y = - \dfrac{1}{4}{x^2}\) |
-4 |
-1 |
0 |
1 |
4 |
Vẽ đồ thị hàm số \(y = \dfrac{1}{2}x - 2\)
+) Cho \(x = 0 \Rightarrow y = - 2\).
+) Cho \(x = 2 \Rightarrow y = - 1\).
b) Xét phương trình hoành độ giao điểm giữa (P) và (d) ta có:
\( - \dfrac{1}{4}{x^2} = \dfrac{1}{2}x - 2 \)
\(\Leftrightarrow {x^2} + 2x - 8 = 0\,\,\left( * \right)\)
Ta có \(\Delta ' = {1^2} - 1.\left( { - 8} \right) = 9 > 0 \Rightarrow \) Phương trình (*) có 2 nghiệm phân biệt
\(\left\{ \begin{array}{l}{x_1} = \dfrac{{ - 1 + 3}}{1} = 2 \Rightarrow {y_1} = - 1 \Rightarrow A\left( {2; - 1} \right)\\{x_2} = \dfrac{{ - 1 - 3}}{1} = - 4 \Rightarrow {y_2} = - 4 \Rightarrow B\left( { - 4; - 4} \right)\end{array} \right.\)
Vậy (d) cắt (P) tại 2 điểm phân biệt \(A\left( {2; - 1} \right)\) và \(B\left( { - 4; - 4} \right)\).
soanvan.me
