Đề bài
Cho tam giác \(ABC\) có \(BC = 7,\) \(\widehat {ABC} = 42^\circ ,\widehat {ACB} = 35^\circ .\) Gọi \(H\) là chân đường cao của tam giác \(ABC\) kẻ từ \(A.\) Hãy tính \(AH\) ( làm tròn kết quả đến chữ số thập phân thứ ba).
Phương pháp giải - Xem chi tiết
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết
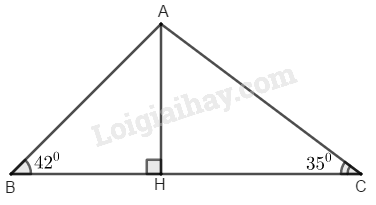
Đặt \(AH = h\).
Xét tam giác vuông ABH, ta có:
\( BH = AH.\cot \widehat {ABH} = h\cot 42^\circ \)
Xét tam giác vuông ACH, ta có:
\( CH = AH.\cot \widehat {ACH} = h\cot 35^\circ \)
\(H\) thuộc đoạn \(BC\) (vì \(35^0,\, 42^0\) đều là góc nhọn), do đó:
\(7 = BC = BH + CH \)
\(= h (\cot\,42^0 + \cot\,35^0),\) suy ra
\(\eqalign{
& h = {7 \over {\cot 42^o + \cot 35^o}} \cr
& = {7 \over {\tan 48^o + \tan 55^o}} \approx 2,757. \cr} \)
soanvan.me
