Đề bài
Tam giác \(ABC\) vuông tại \(A\) có \(AB = 21cm\), \(\widehat C = 40^\circ \). Hãy tính các độ dài:
a) \(AC\) ; b) \(BC\) ;
c) Phân giác \(BD.\)
Phương pháp giải - Xem chi tiết
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Suy ra cạnh huyền bằng cạnh góc vuông chia sin góc đồi hoặc chia cos góc kề.
Lời giải chi tiết
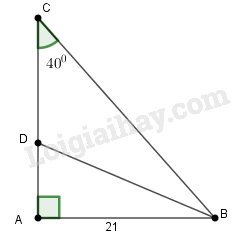
a) Trong tam giác vuông ABC ta có: \(AC = AB.\cot g\widehat C\)\( = 21.\cot g40^\circ \approx 25,0268\left( {cm} \right)\)
b) Trong tam giác vuông ABC ta có: \(BC = \dfrac{{AB}}{{\sin \widehat C}} = \dfrac{{21}}{{\sin 40^\circ }}\)\( \approx 32,6702\left( {cm} \right)\)
c) Vì \(\Delta ABC\) vuông tại \(A\) nên \(\widehat B + \widehat C = 90^\circ \)
Suy ra: \(\widehat B = 90^\circ - \widehat C = 90^\circ - 40^\circ = 50^\circ \)
Vì \(BD\) là phân giác của góc \(B\) nên:
\(\widehat {ABD} = \dfrac{1}{ 2}\widehat B = \dfrac{1 }{2}.50^\circ = 25^\circ \)
Trong tam giác vuông \(ABD\), ta có:
\(BD = \dfrac{{AB}}{{{\rm{cos}}\widehat {ABD}}} = \dfrac{{21}}{{\cos 25^\circ }}\)\( \approx 23,1709\left( {cm} \right)\)
soanvan.me
