Đề bài
Cho hình:
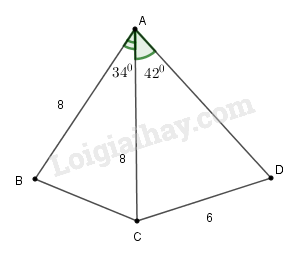
Biết:
\(AB = AC = 8cm, CD = 6cm,\) \(\widehat {BAC} = 34^\circ \) và \(\widehat {CAD} = 42^\circ .\) Tính
a) Độ dài cạnh \(BC;\)
b) \(\widehat {ADC}\);
c) Khoảng cách từ điểm \(B\) đến cạnh \(AD.\)
Phương pháp giải - Xem chi tiết
Cho hình vẽ:

Ta có: \(AB=BC. \sin \alpha \)
Lời giải chi tiết
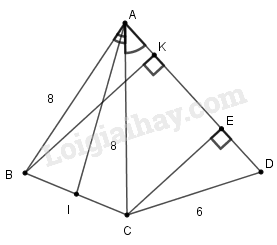
a) Kẻ \(AI \bot BC\)
Vì \(\Delta ABC\) cân tại A nên AI vừa là đường cao, vừa là đường trung tuyến, đường phân giác nên:
\(BI = CI = \dfrac{1}{ 2}BC\)
và \(\widehat {BAI} = \dfrac{1}{ 2}\widehat {BAC} = \dfrac{1}{2}.34^\circ = 17^\circ \)
Trong tam giác vuông \(AIB\), ta có:
\(BI = AB.\sin \widehat {BAI}\)\( = 8.\sin 17^\circ \approx 2,339\left( {cm} \right)\)
\(BC = 2.BI = 2.2,339 = 4,678\left( {cm} \right)\)
b) Kẻ \(CE \bot AD\) \(\left( {E \in AD} \right)\)
Trong tam giác vuông \(CEA\), ta có:
\(CE = AC.\sin \widehat {CAE}\)\( = 8.\sin 42^\circ \approx 5,353\left( {cm} \right)\)
Trong tam giác vuông \(CED\), ta có:
\(\sin \widehat {ACD} = \dfrac{{CE}}{{CD}} = \dfrac{{5,353}}{6}\)\( \approx 0,8922 \Rightarrow \widehat {ADC} \approx 63^\circ 9'\)
c) Kẻ \(BK \bot AD\) \(\left( {K \in AD} \right)\)
\(\widehat {BAK} = \widehat {BAC} + \widehat {CAK} \)\(= {34^0} + {42^0} = {76^0}\)
Trong tam giác vuông \(ABK\), ta có:
\(BK = AB.\sin \widehat {BAK}\)\( = 8.\sin 76^\circ \approx 7,762\left( {cm} \right)\)
soanvan.me
