Đề bài
a) Vẽ hình vuông cạnh \(4 cm\)
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính \(R\) của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính \(r\) của đường tròn này.
Phương pháp giải - Xem chi tiết
+ Giao hai đường chéo hình vuông vừa là tâm đường tròn ngoại tiếp, vừa là tâm đường tròn nội tiếp hình vuông đó.
+ Từ đó tính bán kính theo định lý Pytago
Lời giải chi tiết
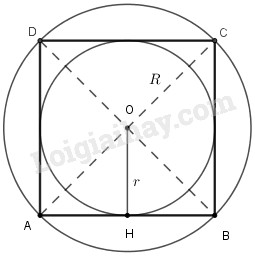
Ta gọi \(a = 4cm\) là cạnh hình vuông.
a) Vẽ hình vuông \(ABCD\) cạnh \(4cm\) bằng thước kẻ.
b) Gọi \(O\) là giao của hai đường chéo \(AC\) và \(BD\) của hình vuông.
Lấy \(O\) là tâm, vẽ đường tròn bán kính \(R = OA,R = OA = 2cm.\)
Vì hình vuông cạnh là \(a\) nên ta có đường chéo \(AC = 4\sqrt 2 cm.\)
Vậy \(R = 2\sqrt 2 cm.\)
c) Kẻ \(OH \bot CD.\)
Lấy \(O\)làm tâm, vẽ đường tròn bán kính \(OH.\)
Vì \(O\) là tâm đường tròn ngoại tiếp hình vuông \(ABCD\) và là tâm của đường tròn nội tiếp hình vuông \(ABCD.\)
Ta có \(r = OH,\) xét \(\Delta COD\) vuông cân tại \(O.\) Do đó, \(OH\) vừa là đường cao, vừa là đường trung trực nên ta có \(OH = HC = HD,\) mà \(CD = 4cm.\)
\( \Rightarrow r = OH = 2cm.\)
soanvan.me
