Đề bài
Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\) và tia phân giác của góc \(A\) cắt đường tròn tại \(M\). Vẽ đường cao \(AH\). Chứng minh rằng:
a) \(OM\) đi qua trung điểm của dây \(BC\)
b) \(AM\) là tia phân giác của góc \(OAH\)
Phương pháp giải - Xem chi tiết
+ Sử dụng : “ Đường kính đi qua điểm chính giữa một cung thì vuông góc và đi qua trung điểm của dây căng cung đó”
+ Sử dụng tính chất hai đường thẳng song song và tính chất tam giác cân.
Lời giải chi tiết
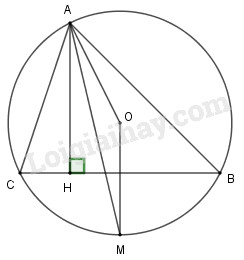

a) \(AM\) là tia phân giác góc \(A\) \(\Rightarrow \widehat {BAM} = \widehat {CAM}\)
Vì \(\widehat {BAM}\) và \(\widehat {MAC}\) là hai góc nội tiếp \( \Rightarrow \overparen{BM}=\overparen{MC}\) hay \(M\) là điểm chính giữa của cung \(BC.\)
Theo định lý về đường kính đi qua điểm chính giữa của một cung ta có \(OM \bot BC\) và \(OM\) đi qua trung điểm dây \(BC\).
b) Theo câu a) ta có \(OM \bot BC\)
Theo giả thiết \(AH \bot BC\)
Vậy \(AH//OM\)
Do đó, \(\widehat {OMA} = \widehat {MAH}\) (so le trong) .
Mặt khác, \(\Delta AOM\) cân vì \(OM = OA\).
Do đó, ta có \(\widehat {MAO} = \widehat {AMO}\)
hay \(AM\) là tia phân giác của góc \(OAH.\)
soanvan.me
