Đề bài
I-Phần trắc nghiệm khách quan
Hãy chọn đáp án đúng:
Câu 1 (0,5 điểm) : Một phương trình bậc nhất hai ẩn:
(A) Luôn có một nghiệm duy nhất
(B) Luôn có vô số nghiệm
(C) Có thể có nghiệm duy nhất
(D) Không thể có vô số nghiệm
Câu 2 (0,5 điểm) : Phương trình bậc nhất hai ẩn 0x + 3y = 12 có tập nghiệm là:
(A) \(S = \left\{ 4 \right\}\) (B) \(S = \left\{ {\left( {0\,\,;\,\,4} \right)} \right\}\)
(C) \(S = \left\{ {\left( {0\,\,;\,\,4} \right)\left| {x \in R} \right.} \right\}\) (D) \(S = \left\{ {\left( {0\,\,;\,\,4} \right)\left| {y \in R} \right.} \right\}\)
Câu 3 (0,5 điểm): Hai cặp số (0 ; 2) và (1 ; -2) là hai nghệm của một phương trình bậc nhất hai ẩn. Tập nghiệm của phương trình đó là:
(A) \(S = \left\{ {\left( {x\,\,;\,\, - 2} \right)\left| {x \in R} \right.} \right\}\)
(B) \(S = \left\{ {\left( {0\,\,;\,\,y} \right)\left| {y \in R} \right.} \right\}\)
(C) \(S = \left\{ {\left( {1\,\,;\,\,y} \right)\left| {y \in R} \right.} \right\}\)
(D) \(S = \left\{ {\left( {0\,\,;\,\, - 2} \right);\left( {1\,\,;\,\, - 2} \right)} \right\}\)
Câu 4 (0,5 điểm): Một nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 2\\\left( {2 - \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y = 2\end{array} \right.\) là:
(A) (4 ; 5) (B) (-2 ; -4)
(C) (0 ; -1) (D) (2 ; 2)
Câu 5 (0,5 điểm): Cho hai hệ phương trình \((I)\,\,\left\{ \begin{array}{l}x - y = 3\\y = x - 3\end{array} \right.\) và \((II)\,\,\left\{ \begin{array}{l}x = 2y + 1\\y = 2x + 1\end{array} \right.\)
Khi đó:
(A) Hệ (I) có một nghiệm duy nhất và hệ (II) có một nghiệm duy nhất.
(B) Hệ (I) có vô số nghiệm và hệ (II) có một nghiệm duy nhất.
(C) Hệ (I) có một nghiệm duy nhất và hệ (II) có vô số nghiệm.
(D) Hệ (I) có vô số nghiệm và hệ (II) có vô số nghiệm.
Câu 6 (0,5 điểm): Đường thẳng (d) trong hình 10 biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn sau:
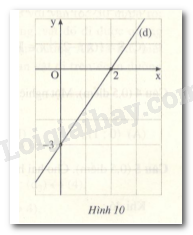
(A) 2x – 3y – 6 = 0
(B) -2y – 3x – 6 = 0
(C) 2y – 3x + 6 = 0
(D) -2y + 3x + 6 = 0
(II) Phần tự luận
Câu 7 (4 điểm): Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2x - 3y = 1\\ - x + 4y = 7\end{array} \right.\)
b) \(\left\{ \begin{array}{l}\sqrt 2 x + y = 1 + \sqrt 2 \\x + \sqrt 2 y = - 1\end{array} \right.\)
Câu 8 (3 điểm): Tìm số tự nhiên có hai chữ số, biết rằng chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 nếu viết thêm chữ số 0 vào giữa chữ số hàng chục và chữ số hàng đơn vị thì ta thu được một số mới lớn hơn số ban đầu là 630.
Lời giải chi tiết
I-Phần trắc nghiệm khách quan
Câu 1: B Câu 2: C Câu 3: A
Câu 4: D Câu 5: B Câu 6: C
Câu 1: Chọn B
Phương pháp
Sử dụng kiến thức về phương trình bậc nhất hai ẩn tại đây.
Lời giải
Phương trình bậc nhất hai ẩn \({\rm{ax}} + by = c\left( {a.b \ne 0} \right)\) luôn có vô số nghiệm.
Câu 2: Chọn C
Phương pháp
Xét phương trình bậc nhất hai ẩn \({\rm{ax}} + by = c\)
Nếu a=0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.\)
Hay tập nghiệm của phương trình là \(S = \left\{ {\left( {x;\dfrac{c}{b}} \right)|x \in \mathbb{R}} \right\}\)
Lời giải
Ta có \(0x + 3y = 12 \Leftrightarrow y = 4\)
Phương trình có tập nghiệm \(S = \left\{ {\left( {x;4} \right)|x \in \mathbb{R}} \right\}\).
Câu 3: Chọn A
Phương pháp
Dựa vào nhận xét: Phương trình bậc nhất hai ẩn luôn có vô số nghiệm
Và phương trình bậc nhất hai ẩn \({\rm{ax}} + by = c\) có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.\) với a=0 và b≠0.
Khi đó tập nghiệm của phương trình là \(S = \left\{ {\left( {x;\dfrac{c}{b}} \right)|x \in \mathbb{R}} \right\}\)
Lời giải
Vì hai cặp số \(\left( {0; - 2} \right)\) và \(\left( {1; - 2} \right)\) là hai nghiệm của một phương trình bậc nhất hai ẩn nên các cặp số \(\left\{ \begin{array}{l}x \in R\\y = - 2\end{array} \right.\) đều là nghiệm của phương trình đó. Suy ra, tập nghiệm của phương trình này là \(S = \left\{ {\left( {x; - 2} \right)|x \in \mathbb{R}} \right\}\)
Câu 4: Chọn D
Phương pháp
Giải hệ phương trình bằng phương pháp thế
Lời giải
Ta có \(\left\{ \begin{array}{l}3x - 2y = 2\\\left( {2 - \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{3x - 2}}{2}\\\left( {2 - \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right).\dfrac{{3x - 2}}{2} = 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{3x - 2}}{2}\\\left( {4 - 2\sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)\left( {3x - 2} \right) = 4\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{3x - 2}}{2}\\\left( {4 - 2\sqrt 3 } \right)x - \left( {3 - 3\sqrt 3 } \right)x + 2 - 2\sqrt 3 = 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{3x - 2}}{2}\\\left( {1 + \sqrt 3 } \right)x = 2 + 2\sqrt 3 \end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;2} \right)\).
Chú ý:
Các em có thể thay từng cặp số ở đáp án vào để kiểm tra xem nó có là nghiệm của hệ hay không.
Cặp số \(\left( {{x_0};{y_0}} \right)\) là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) khi \(\left\{ \begin{array}{l}a{x_0} + b{y_0} = c\\a'{x_0} + b'{y_0} = c'\end{array} \right.\)
Câu 5: Chọn B
Phương pháp
Sử dụng phương pháp thế hoặc cộng đại số giải từng hệ phương trình rồi kết luận
Lời giải
Ta xét hệ (I) \(\left\{ \begin{array}{l}x - y = 3\\y = x - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = x - 3\\y = x - 3\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}0 = 0\,\left( {ld} \right)\\y = x - 3\end{array} \right.\)
Suy ra hệ (I) có vô số nghiệm \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = x - 3\end{array} \right.\)
Ta xét hệ (II) \(\left\{ \begin{array}{l}x = 2y + 1\\y = 2x + 1\end{array} \right.\)\(\Leftrightarrow \left\{ \begin{array}{l}x = 2y + 1\\y = 2\left( {2y + 1} \right) + 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x = 2y + 1\\y = 4y + 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = - 1\\x = - 1\end{array} \right.\)
Vậy hệ phương trình (II) có nghiệm duy nhất \(\left( {x;y} \right) = \left( { - 1; - 1} \right)\)
Chú ý:
Các em cũng có thể dự đoán số nghiệm của hệ phương trình mà không cần giải hệ.
Tập nghiệm của hệ phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,\,\\a'x + b'y = c'\,\,\,\end{array} \right.\) được biểu diễn bởi tập hợp các điểm chung của hai đường thẳng \(d:ax + by = c\) và \(d':a'x + b'y = c'.\)
Trường hợp 1. \(d \cap d' = A\left( {{x_0};{y_0}} \right) \Leftrightarrow \) Hệ phương trình có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\);
Trường hợp 2. \(d//d' \Leftrightarrow \) Hệ phương trình vô nghiệm;
Trường hợp 3. \(d \equiv d' \Leftrightarrow \) Hệ phương trình có vô số nghiệm.
Câu 6: Chọn C
Phương pháp
Xác định hai điểm thuộc đồ thị hàm số.
Ta xác định phương trình đường thẳng \(\left( d \right)\,\)
Từ đó sử dụng tập nghiệm của phương trình \({\rm{ax}} + by = c\) được biểu diễn bởi đường thẳng \(d:{\rm{ }}ax + by = c.\)
Lời giải
Từ đồ thị hàm số ta thấy hai điểm có tọa độ \(\left( {0; - 3} \right);\left( {2;0} \right)\) thuộc đường thẳng \(\left( d \right).\)
Gọi phương trình đường thẳng \(\left( d \right):y = ax + b\left( {a \ne 0} \right)\)
Thay \(x = 0;y = - 3\) vào phương trình \(y = ax + b\) ta được \( - 3 = a.0 + b \Rightarrow b = - 3\)
Thay \(x = 2;y = 0\) vào phương trình \(y = ax + b\) ta được \(0 = 2a + b\) mà \(b = - 3 \Rightarrow 2a - 3 = 0 \)\(\Leftrightarrow a = \dfrac{3}{2}\)(TM )
Vậy phương trình đường thẳng \(\left( d \right):y = \dfrac{3}{2}x - 3\)
Hay đường thẳng \(\left( d \right)\) biểu diễn tập nghiệm của phương trình \(y = \dfrac{3}{2}x - 3 \)\(\Leftrightarrow 2y = 3x - 6\)\( \Leftrightarrow 2y - 3x + 6 = 0\)
Chú ý:
Các em có thể làm theo cách sau:
Xác định hai điểm thuộc đồ thị hàm số.
Thay tọa độ hai điểm đó vào mỗi phương trình ở đáp án để xác định xem cặp số đó có là nghiệm hay không.
Cặp số \(\left( {{x_0};{y_0}} \right)\) là một nghiệm của phương trình \(ax + by + c = 0 \Leftrightarrow a{x_0} + b{y_0} + c = 0\)
(II) Phần tự luận
Câu 7
Phương pháp
Sử dụng phương pháp thế hoặc cộng đại số để giải hệ phương trình
Lời giải
a) \(\left\{ \begin{array}{l}2x - 3y = 1\\ - x + 4y = 7\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}2x - 3y = 1\\ - 2x + 8y = 14\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}2x - 3y + \left( { - 2x + 8y} \right) = 1 + 14\\2x - 3y = 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}5y = 15\\2x - 3y = 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = 3\\2x - 3.3 = 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = 3\\x = 5\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {5;3} \right)\)
b) \(\left\{ \begin{array}{l}\sqrt 2 x + y = 1 + \sqrt 2 \\x + \sqrt 2 y = - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\sqrt 2 x + y = 1 + \sqrt 2 \\\sqrt 2 x + 2y = - \sqrt 2 \end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l} - y = 1 + 2\sqrt 2 \\x + \sqrt 2 y = - 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = - 2\sqrt 2 - 1\\x + \sqrt 2 \left( { - 2\sqrt 2 - 1} \right) = - 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = - 2\sqrt 2 - 1\\x - 4 - \sqrt 2 = - 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = - 2\sqrt 2 - 1\\x = 3 + \sqrt 2 \end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {3 + \sqrt 2 ; - 2\sqrt 2 - 1} \right)\)
Câu 8
Phương pháp
Giải bài toán bằng cách lập hệ phương trình
Ta sử dụng các kiến thức liên quan đến cấu tạo số để lập hệ phương trình
Biểu diễn số có hai chữ số : \(\overline {ab} = 10a + b\) trong đó \(a\) là chữ số hàng chục và \(0 < a \le 9\), \(a \in \mathbb{N}\), \(b\) là chữ số hàng đơn vị và \(0 \le b \le 9,b \in \mathbb{N}\).
Lời giải
Gọi số cần tìm là \(\overline {ab} \,\left( {0 < a \le 9;\,0 \le b \le 9;\,a,b \in \mathbb{N}} \right)\)
Vì chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 nên ta có phương trình \(a - b = 2\) (1)
Viết thêm chữ số \(0\) vào giữa chữ số hàng chục và hàng đơn vị ta được số mới là \(\overline {a0b} \) lớn hơn số ban đầu là \(630\) nên ta có phương trình \(\overline {a0b} - \overline {ab} = 630 \)\(\Leftrightarrow 100a + b - \left( {10a + b} \right) = 630 \)\(\Leftrightarrow 90a = 630\) (2)
Từ (1) và (2) ta có hệ \(\left\{ \begin{array}{l}a - b = 2\\90a = 630\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}a = 7\\b = a - 2\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}a = 7\\b = 5\end{array} \right.\,\left( {TM} \right)\)
Vậy số cần tìm là \(75.\)
soanvan.me
