Đề bài
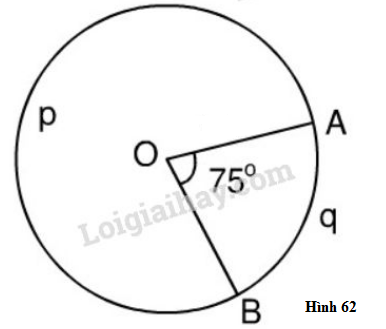
Trong hình 62, đường tròn tâm \(O\) có bán kính \(R = 2m,\,\,\widehat {AOB} = {75^o}\)
a) Tính sđ \(\overparen{ApB}\)
b) Tính độ dài các cung \(AqB\) và \(ApB\)
c) Tính diện tích hình quạt tròn \(OAqB\)
Phương pháp giải - Xem chi tiết
a) + Số đo góc ở tâm bằng số đo cung bị chắn
+ Số đo cung lớn bằng \(360^\circ \)\( - \) số đo cung nhỏ.
b) Cho hình tròn bán kính \(R\), độ dài cung tròn \(n^\circ \) là \(l = \dfrac{{\pi Rn}}{{180}}\)
Chu vi hình tròn đó là \(C = 2\pi R\)
c) Cho hình tròn bán kính \(R\), diện tích quạt tròn số đo \(n^\circ \) là \(S = \dfrac{{\pi {R^2}n}}{{360}}\)
Lời giải chi tiết
a) Từ giả thiết \(\widehat {AOB} = 75^\circ \) \( \Rightarrow \) sđ\(\overparen{AqB}\)\( = 360^\circ - \) sđ\(\overparen{AB}\)
Vậy sđ\(\overparen{ApB}\)\( = 360^\circ - 75^\circ = 285^\circ \)
b) Gọi \({l_{\overparen{AqB}}},{l_{\overparen{ApB}}}\) lần lượt là độ dài của các cung \(AqB,ApB;C = 2\pi R\) là độ dài đường tròn tâm \(O.\)
Theo công thức tính độ dài cung ta có :
\(\displaystyle {l_{\overparen{AqB}}}\) \(=\displaystyle {{\pi Rn} \over {180}} = {{\pi .2.75} \over {180}} = {5 \over 6}\pi (cm)\)
Vậy \({l_{\overparen{ApB}}} = C - {l_{\overparen{AqB}}} = 4\pi - \dfrac{{5\pi }}{6} \)\(= \dfrac{{19\pi }}{6}\left( {cm} \right).\)
c) Ta có \(\widehat{AOB}\) \( = 75^\circ ;R = 2cm\)
Vậy \({S_{OAqB}} = \dfrac{{\pi {{.2}^2}.75}}{{360}} = \dfrac{{5\pi }}{6}\left( {c{m^2}} \right).\)
soanvan.me
