Đề bài
Các đường cao hạ từ \(A\) và \(B\) của tam giác \(ABC\) cắt nhau tại \(H\) (góc \(C\) khác \(90\)o) và cắt đường tròn ngoại tiếp tam giác \(ABC\) lần lượt tại \(D\) và \(E\). Chứng minh rắng:
a) \(CD = CE\)
b) Tam giác \(BHD\) cân
c) \(CD = CH\)
Phương pháp giải - Xem chi tiết
a) Sử dụng: “Số đo góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn” từ đó suy ra hai cung bằng nhau và hai dây bằng nhau.
b) Chứng minh tam giác \(HBD\) có \(BM\) vừa là đường cao vừa là đường phân giác nên nó là tam giác cân
c) Sử dụng tính chất đường trung trực của đoạn thẳng \(HD.\)
Lời giải chi tiết
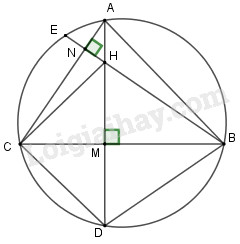
a) Gọi \(M,N\) lần lượt là giao điểm của \(AD\) với \(BC\) và \(BE\) với \(AC.\)
Các góc \(ANB\) và \(AMB\) là hai góc có đỉnh nằm bên trong đường tròn nên ta có :
\(\widehat {ANB} = \dfrac{1}{2}\)(sđ \(\overparen{EC}+\) sđ \(\overparen{AB}\)) \( = 90^\circ \) (vì \(BE \bot AC\))
\(\widehat {AMB} = \dfrac{1}{2}\) (sđ\(\overparen{DC}+\) sđ \(\overparen{AB}\)) \( = 90^\circ \) (vì \(AD \bot BC\))
Vậy ta có sđ\(\overparen{CE}=\) sđ\(\overparen{CD}\)\( \Leftrightarrow CD = CE\)
b) Các góc \(EBC\) và \(CBD\) là hai góc nội tiếp nên ta có :
\(\widehat {EBC} = \dfrac{1}{2}\) sđ\(\overparen{EC}\) và \(\widehat {CBD} = \dfrac{1}{2}\) sđ\(\overparen{DC}\)
Theo câu a) ta có \(\overparen{CD}=\overparen{CE}\), suy ra \(\widehat {EBC} = \widehat {CBD}.\)
Do đó, \(BM\) vừa là đường cao vừa là đường phân giác của \(\Delta BHD\).
Vậy \(\Delta BHD\) cân .
c) Vì \(\Delta BHD\) cân nên \(BM\) là đường trung trực của đoạn \(HD \Rightarrow MH = MD.\)
Xét \(\Delta HMC\) và \(\Delta DMC\) vuông tại \(M\) và \(CM\) là cạnh chung; \(MH = MD.\)
Vậy \(\Delta HMC = \Delta DMC \) \( \Rightarrow CD = CH.\)
soanvan.me
