Đề bài
Cho đường tròn \((O)\) và một điểm \(A\) cố định trên đường tròn. Tìm quỹ tích các trung điểm \(M\) của dây \(AB\) khi điểm \(B\) di động trên đường tròn đó.
Phương pháp giải - Xem chi tiết
+ Phần thuận: Lập luận để có \(\widehat {AMO} = 90^\circ \) suy ra quỹ tích điểm \(M\) là đường tròn đường kính \(AO.\)
+ Chứng minh phần đảo và kết luận.
Lời giải chi tiết

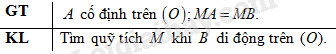
Phần thuận:
Kẻ đường kính \(AC;\) kẻ dây \(AB\); nối \(MO.\) Các điểm \(A\) và \(O\) cố định. Khi đó, ta có : \(MA = MB\) và \(MO \bot AB\) vì đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc dây đó.
\( \Rightarrow \widehat {AMO} = 90^\circ .\)
Khi \(B\) thay đổi trên cung \(AC\) thì \(M\) luôn nhìn cạnh \(AO\) cố định dưới một góc bằng \(90^\circ \) nên điểm \(M\) thuộc đường tròn đường kính \(AO.\)
Phần đảo:
Lấy điểm \(M'\) bất kì khác \(O\) và \(A\) thuộc đường tròn đường kính \(AO\). Tia \(AM'\) cắt đường tròn đường kính \(AC\) tại \(B'\). Kẻ \(OM'\). Ta phải chứng minh \(M'A = M'B'\).
Thật vậy \(\widehat {AM'O} = 90^\circ \) (vì góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow OM' \bot AB'\) nên \(M'\) là trung điểm đoạn \(AB'\) ( vì đường kính vuông góc với dây thì đi qua trung điểm dây đó)
Suy ra \(AM' = M'B'\).
Kết luận:
Quỹ tích các điểm \(M\) khi \(B\) di động trên đường tròn \(\left( O \right)\) là đường tròn đường kính \(AO.\)
soanvan.me
