Đề bài
Cho hình bình hành \(ABCD ,\) các đường chéo cắt nhau tại \(O.\) Gọi \(E, F\) theo thứ tự là trung điểm của \(OD, OB.\) Gọi \(K\) là giao điểm của \(AE\) và \(CD.\) Chứng minh rằng:
\(a)\) \(AE\) song song \(CF\)
\(b)\) \(DK =\displaystyle {1 \over 2}KC\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
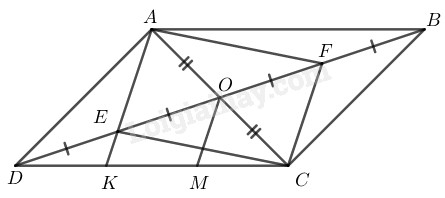
\(a)\) Vì ABCD là hình bình hành nên \(OB = OD\) (tính chất hình bình hành)
\(OE = \displaystyle {1 \over 2}OD\;\; \) (vì E là trung điểm của OD)
\(OF =\displaystyle {1 \over 2}OB\;\;\) (vì F là trung điểm của OB)
Suy ra: \(OE = OF\)
Xét tứ giác \(AECF,\) ta có:
\(OE = OF\) (chứng minh trên)
\(OA = OC\) (vì \(ABCD\) là hình bình hành)
Suy ra: Tứ giác \(AECF\) là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường )
\(⇒ AE // CF\)
\(b)\) Kẻ \(OM // AK\)
Trong \(∆ CAK\) ta có:
\(OA = OC\) ( chứng minh trên)
\(OM // AK\) ( theo cách vẽ)
\(⇒ CM = MK\) (tính chất đường trung bình của tam giác) \((1)\)
Trong \(∆ DMO\) ta có:
\(DE = EO \;\;\) (vì E là trung điểm của OD)
\(EK // OM\) (do \(OM // AK\))
\(⇒ DK = KM\) (tính chất đường trung bình của tam giác) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(DK = KM = MC\)
\(⇒ DK = \displaystyle {1 \over 2}KC\)
soanvan.me
