Đề bài
Cho hình bình hành \(ABCD.\) Gọi \(E\) là trung điểm của \(AB,\) \(F\) là trung điểm của \(CD.\) Chứng minh rằng \(DE = BF.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Trong hình bình hành, các cạnh đối bằng nhau.
Dấu hiệu nhận biết:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
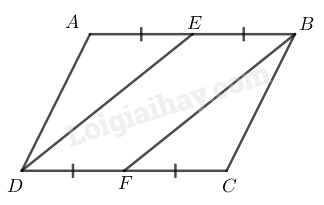
Vì ABCD là hình bình hành nên \(AB = CD\) ( tính chất hình bình hành)
Lại có E là trung điểm cạnh AB và F là trung điểm cạnh CD nên:
\(\eqalign{ & EB = {1 \over 2}AB\;\;(gt) \cr & FD = {1 \over 2}CD\;\;(gt) \cr} \)
Suy ra: \(EB = FD \;\;(1)\) (vì \(AB = CD)\)
Mà \(AB // CD\;\;\; (gt)\)
\(⇒ BE // FD \;\;\; (2)\)
Từ \((1)\) và \((2)\) suy ra tứ giác \(BEDF\) là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
\(⇒ DE = BF\) (tính chất hình bình hành)
soanvan.me
