Đề bài
Cho tam giác \(ABC.\) Dựng đường thẳng song song với \(BC,\) cắt cạnh \(AB\) ở \(E,\) cắt cạnh \(AC\) ở \(F\) sao cho \(BE = AF.\)
Phương pháp giải - Xem chi tiết
+) Cách dựng: Nêu thứ tự từng bước dựng hình, đòng thời thể diện các nét dựng trên hình vẽ.
+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.
Lời giải chi tiết
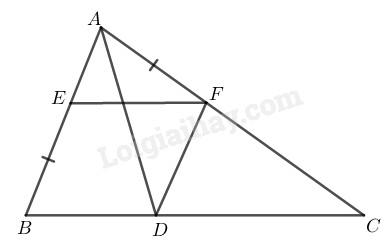
Cách dựng:
- Dựng đường phân giác \(AD\) của góc BAC.
- Qua \(D\) dựng đường thẳng song song \(AB\) cắt \(AC\) tại \(F.\)
- Qua \(F\) dựng đường thẳng song song với \(BC\) cắt \(AB\) tại \(E.\)
Ta có điểm \(E, F\) cần dựng.
Chứng minh:
Vì \(DF // AB\)
\( \Rightarrow {\widehat {EAD}} = {\widehat {ADF}}\) (so le trong)
\({\widehat {EAD}} = {\widehat {FAD}}\) (vì AD là tia phân giác của góc BAC)
Suy ra: \({\widehat {ADF}} = {\widehat {FAD}}\)
\(⇒ ∆ AFD\) cân tại \(F\)
\(⇒ AF = DF \;\;(1)\)
Ta có: \(DF // AB\) hay \(DF // BE\)
\(EF // BC\) hay \(EF // BD\)
Suy ra tứ giác \(BDFE\) là hình bình hành (định nghĩa)
\(⇒ BE = DF\;\; (2)\)
Từ \((1)\) và \((2)\) suy ra: \(AF = BE\)
soanvan.me
