Dựng hình bình hành \(ABCD,\) biết:
LG a
\(\) \(AB = 2cm,\) \(AD = 3cm,\) \(\widehat A = {110^0}\)
Phương pháp giải:
+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.
+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.
+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài
Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.
Lời giải chi tiết:
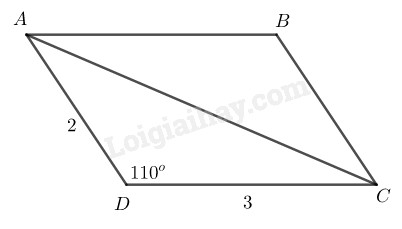
\(\) Cách dựng:
- Dựng \(∆ ABD\) có \(AB = 2cm,\) \(\widehat A = {110^0},\) \(AD = 3cm\)
- Dựng tia đi qua B và \(// AD\), dựng tia đi qua D và \(// AB\). Hai tia này cắt nhau tại \(C\)
Ta có hình bình hành \(ABCD\) cần dựng
Chứng minh: \(AB // CD,\) \(AD // BC\) nên tứ giác \(ABCD\) là hình bình hành.
Ta lại có \(AB = 2cm,\) \(\widehat A = {110^0},\) \(AD = 3cm.\) Bài toán có một nghiệm hình.
LG b
\(\) \(AC = 4cm,\) \(BD = 5cm,\) \(\widehat {BOC} = {50^0}\) (\(O\) là giao điểm của hai đường chéo).
Phương pháp giải:
+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.
+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.
+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài
Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.
Lời giải chi tiết:
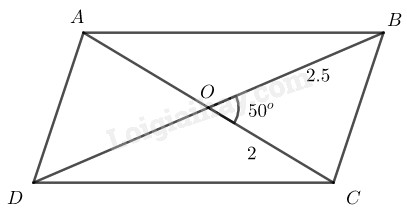
Cách dựng:
- Dựng \(∆ OBC\) có \(OC = 2cm,\) \(OB = 2,5cm ,\) \(\widehat {BOC} = {50^0}\)
- Trên tia đối tia \(OC\) lấy điểm \(A\) sao cho \(OA = OC = 2cm\)
- Trên tia đối tia \(OB\) lấy điểm \(D\) sao cho \(OD = OB = 2,5cm\)
Nối \(AB, BC, CD, AD\) ta có hình bình hành \(ABCD\) cần dựng
Chứng minh: Tứ giác \(ABCD\) có \(OA = OC,\) \(OB = OD\) nên nó là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Có \(AC =OA+OC= 4cm,\) \(BD =OB+OD= 5cm,\) \(\widehat {BOC} = {50^0}\)
Bài toán có một nghiệm hình.
soanvan.me
