Đề bài
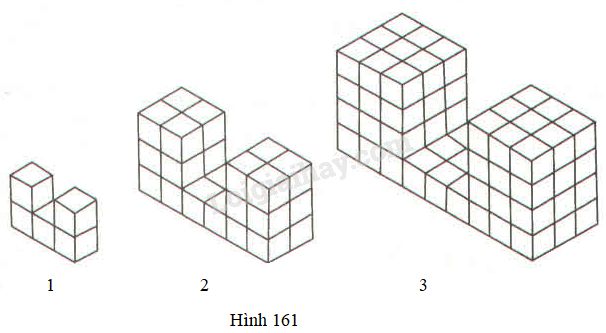
Hãy quan sát ba hình dưới đây (h.161), trong đó có các hình lập phương đơn vị được xếp theo dạng chữ U.
Số các hình lập phương đã xếp tăng lên theo quy luật \(5\) hình → \(28\) hình → \(81\) hình.
Nếu theo quy luật này thì có bao nhiêu hình lập phương đơn vị ở hình thứ \(10\)?
Phương pháp giải - Xem chi tiết
Ta tìm quy luật tính số hình lập phương đơn vị của các hình như sau:
Số hình lập phương đơn vị ở hình \(1\) là:
\(1^2.3+1^2.1.2=5\) (khối)
Số hình lập phương đơn vị ở hình \(2\) là:
\({2^2}.3 + {2^2}.2.2 = 28\) (khối)
Số hình lập phương đơn vị ở hình \(3\) là:
\({3^2}.3 + {3^2}.3.2 = 81\) (khối)
\( \Rightarrow \) Công thức tính số hình lập phương ở hình \(x\) là: \({x^2}.3 + {x^2}.x.2\).
Từ đó ta tính được số hình lập phương đơn vị ở hình \(10\).
Lời giải chi tiết
Số hình lập phương đơn vị ở hình \(1\) là:
\(1^2.3+1^2.1.2=5\) (khối)
Số hình lập phương đơn vị ở hình \(2\) là:
\({2^2}.3 + {2^2}.2.2 = 28\) (khối)
Số hình lập phương đơn vị ở hình \(3\) là:
\({3^2}.3 + {3^2}.3.2 = 81\) (khối)
\( \Rightarrow \) Công thức tính số hình lập phương ở hình \(x\) là: \({x^2}.3 + {x^2}.x.2\).
Số hình lập phương đơn vị ở hình \(10\) là:
\({10^2}.3 + {10^2}.10.2 = 2300\) (khối)
Cách khác:
Ở hình thứ 3, ta có:
Số hình lập phương đơn vị bên trái là \(3.4.3=36\)
Số hình lập phương đơn vị bên phải là \(3.4.3 =36\)
Số hình lập phương đơn vị ở giữa là \(3.3=9\)
Vậy có tổng số : \(36+36+9=81\) hình lập phương đơn vị
Với quy luật đó thì hình thứ 10:
Số hình lập phương đơn vị bên trái là \(10.11.10=1100\)
Số hình lập phương đơn vị bên phải là \(10.11.10=1100\)
Số hình lập phương đơn vị ở giữa là \(10.10 =100\)
Vậy tổng số hình lập phương đơn vị của hình thứ 10 là:
\(1100 + 1100 +100=2300\) (hình)
soanvan.me
