Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu ta tăng
LG a
Gấp đôi chiều cao của hình chóp;
Phương pháp giải:
Sử dụng:
- Diện tích tam giác đều cạnh \(a\) là \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).
- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.
\(V = \dfrac{1}{3} .S.h\)
Trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.
Lời giải chi tiết:
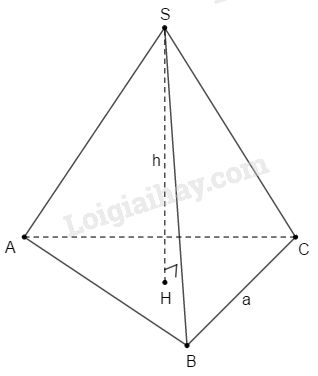
Tam giác đều cạnh a có diện tích bằng \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).
Do đó, hình chóp tam giác đều với cạnh đáy \(a\), chiều cao \(h\) có thể tích là:
\(\displaystyle V = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}h\sqrt 3 } \over {12}}\)
Nếu tăng gấp đôi chiều cao thì thể tích hình chóp là:
\(\displaystyle V' = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.2h = 2.{{{a^2}h\sqrt 3 } \over {12}} = 2V\)
LG b
Gấp đôi cạnh đáy của hình chóp;
Phương pháp giải:
Sử dụng:
- Diện tích tam giác đều cạnh \(a\) là \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).
- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.
\(V = \dfrac{1}{3} .S.h\)
Trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.
Lời giải chi tiết:
Tam giác đều cạnh a có diện tích bằng \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).
Do đó, hình chóp tam giác đều với cạnh đáy \(a\), chiều cao \(h\) có thể tích là:
\(\displaystyle V = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}h\sqrt 3 } \over {12}}\)
Nếu tăng gấp đôi cạnh đáy thì thể tích hình chóp là:
\(\displaystyle V' = {1 \over 3}.{{{{\left( {2a} \right)}^2}\sqrt 3 } \over 4}.h = 4.{{{a^2}h\sqrt 3 } \over {12}} \)\(\,= 4V\)
LG c
Gấp đôi cả chiều cao và cạnh đáy của hình chóp.
Phương pháp giải:
Sử dụng:
- Diện tích tam giác đều cạnh \(a\) là \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).
- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.
\(V = \dfrac{1}{3} .S.h\)
Trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.
Lời giải chi tiết:
Tam giác đều cạnh a có diện tích bằng \(\displaystyle{{{a^2}\sqrt 3 } \over 4}\).
Do đó, hình chóp tam giác đều với cạnh đáy \(a\), chiều cao \(h\) có thể tích là:
\(\displaystyle V = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}h\sqrt 3 } \over {12}}\)
Nếu gấp đôi cả chiều cao và cạnh đáy thì thể tích hình chóp là:
\(\displaystyle V' = {1 \over 3}.{{{{\left( {2a} \right)}^2}\sqrt 3 } \over 4}.2h = 8.{{{a^2}h\sqrt 3 } \over {12}} \)\(\,= 8V\)
soanvan.me
