Đề bài
Một hình chóp tứ giác đều \(S.ABCD\) có độ dài cạnh đáy là \(10cm\), chiều cao hình chóp là \(12cm.\)
Tính:
a) Diện tích toàn phần của hình chóp.
b) Thể tích hình chóp.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao.
\({S_{xq}} = 2p.h\)
Trong đó: \(p\) là nửa chu vi đáy, \(h\) là chiều cao.
- Diện tích toàn phần của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy.
- Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao
\(V = S. h\)
Trong đó: \(S\) là diện tích đáy; \(h\) là chiều cao lăng trụ.
Lời giải chi tiết
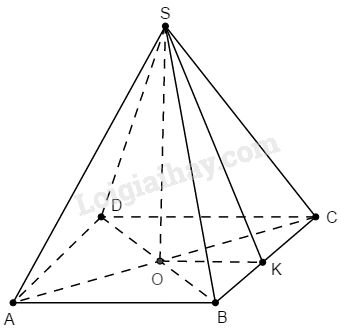
a) Gọi \(O\) là tâm của hình vuông đáy.
Kẻ \(SK ⊥ BC\)
Vì tam giác SBC cân tại S nên SK vừa là đường cao vừa là đường trung tuyến, hay K là trung điểm của BC
Do đó: \(KB = KC =BC:2= 5 \;cm\)
Vì \(SO ⊥ (ABCD)\) nên \(SO ⊥ OK\)
Trong tam giác \(SOK\) có \(\widehat {SOK} = 90^\circ \); \(OK = \displaystyle{1 \over 2}AB = 5\;(cm)\) (vì OK là đường trung bình của tam giác ABC)
Áp dụng định lí Py-ta-go vào tam giác vuông \(SOK,\) ta có:
\(S{K^2} = S{O^2} + O{K^2} = {12^2} + {5^2} = 169\)
\( \Rightarrow SK = 13\; (cm)\).
Diện tích xung quanh hình chóp đều là:
\(S_{xq} = \left( {2.10} \right).13 = 260\;(c{m^2})\)
Diện tích mặt đáy là: \(S = 10.10 = 100\;(c{m^2})\)
Diện tích toàn phần hình chóp đều là:
\({S_{TP}} = 260 + 100 = 360\;(c{m^2})\)
b) Thể tích hình chóp đều là:
\(V = \displaystyle {1 \over 3}S.h = \displaystyle {1 \over 3}.100.12 = 400\;(c{m^3})\).
soanvan.me
