Đề bài
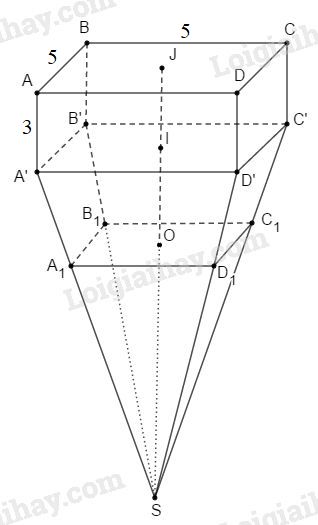
Tính thể tích của một trụ bê tông cho theo các kích thước ở hình \(166,\) \(SJ = 9, OI = IJ.\)
Phần trên là một hình hộp chữ nhật, phần dưới là một hình chóp cụt tứ giác đều.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.
\(V = \dfrac{1}{3} .S.h\)
Trong đó: \(S\) là diện tích đáy, \(h\) là chiều cao.
- Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao
\(V = S. h\)
Trong đó: \(S\) là diện tích đáy; \(h\) là chiều cao lăng trụ.
Lời giải chi tiết
Thể tích phần hình hộp chữ nhật \(ABCD.A'B'C'D'\) là:
\( 5.5.3 = 75\) (đvtt)
Ta có \(IJ = AA’ ⇒ IJ = 3\)
\(\eqalign{ & OI = IJ = 3 \cr & SJ = 9 \Rightarrow SO = 3 \cr} \)
Vì \(SO=OI=3\) \(\Rightarrow S{A_1} = {A_1}A';S{B_1} = {B_1}B'\)
Nên \(A_1B_1\) là đường trung bình của tam giác \(SA'B'\)
Khi đó hình vuông \({A_1}{B_1}{C_1}{D_1}\) có cạnh \(A_1B_1 =\displaystyle {1 \over 2}A'B'\)\(=\displaystyle {1 \over 2}AB = 2,5\)
Thể tích hình chóp đều \(S.A’B’C’D’\) là:
\(\displaystyle {1 \over 3}\left( {5.5} \right).6 = 50\) (đvtt)
Thể tích hình chóp đều \(S.{A_1}{B_1}{C_1}{D_1}\) là:
\(\displaystyle {1 \over 3}\left( {2,5.2,5} \right).3 = 6,25\) (đvtt)
Thể tích hình chóp cụt \(A'B'C'D'.{A_1}{B_1}{C_1}{D_1}\) là:
\( 50 - 6,25 = 43,75\) (đvtt)
Thể tích của trụ bê tông là:
\(V = 43,75 + 75 = 118,75\) (đvtt).
soanvan.me
