Đề bài
Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD, E và F là giao điểm của AK và CI với BD.
a) Chứng minh tứ giác AKCI là hình bình hành.
b) Chứng minh rằng DE = EF = FB.
c) Chứng minh ba đường AC, IK, EF đồng quy.
Lời giải chi tiết
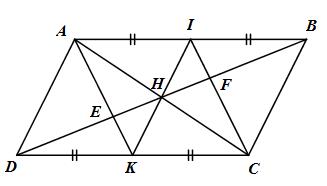
a) Ta có:
\(AI = {1 \over 2}AB\) (I là trung điểm của AB),
\(CK = {1 \over 2}CD\) (K là trung điểm của CD)
Và \(AB = CD\) (ABCD là hình bình hành)
\( \Rightarrow AI = CK\)
Mà AI // CK \((AB // CD, I \in AB,\,\,K \in CD)\)
Do đó tứ giác AICK là hình bình hành.
b) \(\Delta ABE\) có I là trung điểm của AB và \(IF // AE\)
Nên F là trung điểm của EB \( \Rightarrow BF = EF\,\,\left( 1 \right)\)
\(\Delta DCF\) có EK // FC và K là trung điểm của CD
Nên E là trung điểm của DF \( \Rightarrow DE = EF\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(DE = EF = BF\).
c) Gọi H là giao điểm của AC và BD (3)
\( \Rightarrow H\) là trung điểm của AC (ABCD là hình bình hành)
Hình bình hành AICK có H là trung điểm của AC nên H là trung điểm của IK.
\( \Rightarrow IK\) đi qua H (4)
Từ (3) và (4) \( \Rightarrow AC,IK,EF\) đồng quy tại H.
soanvan.me
