Đề bài
Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABCD là hình thoi.
b) Gọi E, F lần lượt là trung điểm của AB và AC. Chứng minh tứ giác AEMF là hình thoi.
Lời giải chi tiết
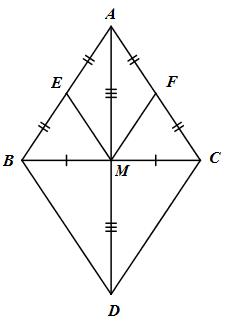
a) Tứ giác ABCD có:
AD và BC cắt nhau tại M (gt);
M là trung điểm của BC (gt)
M là trung điểm của AD (D đối xứng với A qua BC)
Do đó tứ giác ABDC là hình bình hành
Mà \(AD \bot BC\) (vì D đối xứng với A qua BC)
Nên hình bình hành ABDC là hình thoi.
b) Ta có \(AM = {1 \over 2}AB\) (đường trung tuyến ứng với cạnh huyền)
Và \(AE = {1 \over 2}AB\) (E là trung điểm của AB)
\( \Rightarrow EM = EA = {1 \over 2}AB\,\,\left( 1 \right)\)
Ta có \(MF = {1 \over 2}AC\) (đường trung tuyến ứng với cạnh huyền)
Và \(AF = {1 \over 2}AC\) (F là trung điểm của AC)
\( \Rightarrow MF = AF = {1 \over 2}AC\,\,\left( 2 \right)\)
\(AB = AC\) (\(\Delta ABC\) cân tại A) (3)
Từ (1), (2) và (3) suy ra \(EM = EA = MF = AF\).
Do đó tứ giác AEMF là hình thoi.
soanvan.me
