Đề bài
Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC \((E \in AC,F \in AB)\)
a) Chứng minh rằng tứ giác AEDF là hình chữ nhât.
b) Chứng minh rằng tứ giác BFED là hình bình hành.
Lời giải chi tiết
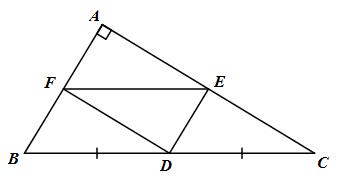
a) Tứ giác AEDF có:
AE // DF (AC // FD, \(E \in AC\))
AF // DE (AB // DE, \(F \in AB\))
\( \Rightarrow AEDF\) là hình bình hành.
Mà \(\widehat {FAE} = {90^0}\) (\(\Delta ABC\) vuông tại A)
Nên AEDF là hình chữ nhât.
b) \(\Delta ABC\) có D là trung điểm của BC và FD // AC \( \Rightarrow F\) là trung điểm của AB.
\(\Delta ABC\) có D là trung điểm của BC và DE // AB \( \Rightarrow E\) là trung điểm của AC
\( \Rightarrow EF\) là đường trung bình của tam giác ABC
\( \Rightarrow EF//BC\) và \(EF = {1 \over 2}BC\)
Lại có \(BD = {1 \over 2}BC\) (Vì D là trung điểm của BC)
\( \Rightarrow EF//BD\) và \(EF = BD\)
Vậy tứ giác BFED là hình bình hành (dấu hiệu nhận biết).
soanvan.me
