Đề bài
Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm cảu các cạnh AB, BC, CD, DA.
a) Chứng minh rằng tứ giác EFGH là hình bình hành.
b) Hai đường chéo AC, BD của tứ giác ABCD cần điều kiện gì để tứ giác EFGH lần lượt là:
- Hình chữ nhật
- Hình thoi
- Hình vuông.
Lời giải chi tiết
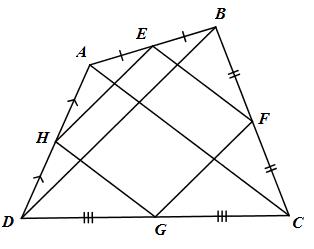
a) E, F lần lượt là trung điểm của AB và BC (gt)
\( \Rightarrow EF\) là đường trung bình của tam giác ABC
\( \Rightarrow EF//AC\) và \(EF = {1 \over 2}AC\,\,\left( 1 \right)\)
H, G lần lượt là trung điểm của AD và DC (gt)
\( \Rightarrow HG\) là đường trung bình của tam giác ACD
\( \Rightarrow HG//AC\) và \(HG = {1 \over 2}AC\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra EF // HG và \(EF = HG\)
Do đó tứ giác EFGH là hình bình hành.
b) Tứ giác EFGH là hình bình hành. EF // AC, \(EF = {1 \over 2}AC\)
Ta còn có EH là đường trung bình của tam giác ABD
\( \Rightarrow EH//BD\) và \(EH = {1 \over 2}BD\)
* Tứ giác EFGH là hình chữ nhật.
\( \Leftrightarrow \) Hình bình hành EFGH có \(\widehat {HEF} = {90^0} \Leftrightarrow HE \bot EF \Leftrightarrow EH \bot AC \Leftrightarrow AC \bot BD\)
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc với nhau thì tứ giác EFGH là hình chữ nhật.
* Tứ giác EFGH là hình thoi.
\( \Leftrightarrow \) Hình bình hành EFGH có \(EF = EH \Leftrightarrow AC = BD\)
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD bằng nhau thì tứ giác EFGH là hình thoi.
* Tứ giác EFGH là hình vuông.
\( \Leftrightarrow \) Hình chữ nhật EFGH có \(EF = EH \Leftrightarrow AC = BD\)
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc và bằng nhau thì tứ giác EFGH là hình vuông.
soanvan.me
