Đề bài
Cho hình thang cân ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD.
a) Chứng minh rằng tứ giác MNPQ là hình thoi.
b) Gọi I là giao điểm của AC và BD. Chứng minh rằng một trong hai đường chéo của hình thoi đi qua I.
Lời giải chi tiết
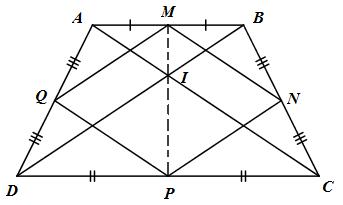
a) Ta có: M, N lần lượt là trung điểm của AB và BC (gt)
\( \Rightarrow MN\) là đường trung bình của tam giác ABC \( \Rightarrow MN//AC\) và \(MN = {1 \over 2}AC\,\,\,\left( 1 \right)\)
Q, P lần lượt là trung điểm của AD và DC (gt)
\( \Rightarrow QP\) là đường trung bình của tam giác ADC \( \Rightarrow QP//AC\) và \(QP = {1 \over 2}AC\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra MN // QP và \(MN = QP\).
Do đó tứ giác NMPQ là hình bình hành.
Mặt khác Q, M lần lượt là trung điểm của AD, AB (gt)
\( \Rightarrow QM\) là đường trung bình của tam giác ABD \( \Rightarrow QM = {{BD} \over 2}\)
Mà \(AC = BD\) (tứ giác ABCD là hình thang cân)
\( \Rightarrow MN = QM\)
Hình bình hành MNPQ có \(MN = QM\) nên là hình thoi.
b) Xét \(\Delta ACD\) và \(\Delta BCD\) có:
\(AD = BC\) (tứ giác ABCD là hình thang cân)
\(AC = BD\) (tứ giác ABCD là hình thang cân)
CD chung
\( \Rightarrow \Delta ACD = \Delta BDC\,\,\,\left( {c.c.c} \right)\)
\( \Rightarrow \widehat {ACD} = \widehat {BDC} \Rightarrow \Delta ICD\) cân tại \(I \Rightarrow IC = ID \Rightarrow I\) thuộc trung trực của CD.
Mặt khác: M, P lần lượt là trung điểm của các cạnh đáy AB, CD của hình thang cân ABCD (AB // CD) (gt)
\( \Rightarrow MP\) là trục đối xứng của hình thang cân ABCD.
\( \Rightarrow MP\) lad đường trung trực của CD,
Do đó \(I \in MP\).
Vậy đường chéo MO của hình thoi MNPQ đi qua I.
soanvan.me
