Kết quả của phép tính \(\left( { - 125} \right).8\) là:
-
A
$1000$
-
B
$ - 1000$
-
C
$ - 100$
-
D
$ - 10000$
Đáp án của giáo viên lời giải hay : B
Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu $\left( - \right)$ trước kết quả nhận được.
\(\left( { - 125} \right).8 = - \left( {125.8} \right) = - 1000\)
Khi \(x = - 12\) , giá trị của biểu thức \(\left( {x - 8} \right).\left( {x + 7} \right)\) là số nào trong bốn số sau:
-
A
\( - 100\)
-
B
\(100\)
-
C
\( - 96\)
-
D
\( - 196\)
Đáp án của giáo viên lời giải hay : B
Thay giá trị của $x$ vào biểu thức rồi áp dụng quy tắc nhân hai số nguyên ta tính được giá trị của biểu thức.
Thay \(x = - 12\) vào biểu thức \(\left( {x - 8} \right).\left( {x + 7} \right)\), ta được:
\(\begin{array}{l}\left( { - 12 - 8} \right).\left( { - 12 + 7} \right)\\ = \left( { - 20} \right).\left( { - 5} \right)\\ = 20.5\\ = 100\end{array}\)
Giá trị biểu thức \(M = \left( { - 192873} \right).\left( { - 2345} \right).{\left( { - 4} \right)^5}.0\) là
-
A
\( - 192873\)
-
B
\(1\)
-
C
\(0\)
-
D
\(\left( { - 192873} \right).\left( { - 2345} \right).{\left( { - 4} \right)^5}\)
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất nhân một số với \(0\): Số nào nhân với \(0\) cũng bằng \(0\)
Vì trong tích có một thừa số bằng \(0\) nên \(M = 0\)
Tính giá trị biểu thức \(P = {\left( { - 13} \right)^2}.\left( { - 9} \right)\) ta có
-
A
\(117\)
-
B
\( - 117\)
-
C
\(1521\)
-
D
\( - 1521\)
Đáp án của giáo viên lời giải hay : D
Thứ tự thực hiện phép tính: Bình phương trước rồi thực hiện phép nhân hai số nguyên.
\(P = {\left( { - 13} \right)^2}.\left( { - 9} \right) = 169.\left( { - 9} \right) = - 1521\)
Tính giá trị biểu thức \(P = \left( {x - 3} \right).3 - 20.x\) khi \(x = 5.\)
-
A
\( - 94\)
-
B
\(100\)
-
C
\( - 96\)
-
D
\( - 104\)
Đáp án của giáo viên lời giải hay : A
Bước 1: Thay giá trị của $x$ vào biểu thức
Bước 2: Tính giá trị của biểu thức
Thay \(x = 5\) vào \(P\) ta được:
\(\begin{array}{l}P = \left( {5 - 3} \right).3 - 20.5\\ = 2.3 - 100 = 6 - 100 = - 94\end{array}\)
Có bao nhiêu giá trị \(x\) nguyên dương thỏa mãn $\left( {x - 3} \right).\left( {x + 2} \right) = 0$ là:
-
A
\(3\)
-
B
\(2\)
-
C
\(0\)
-
D
\(1\)
Đáp án của giáo viên lời giải hay : D
Sử dụng kiến thức: $A.B = 0$ thì $A = 0$ hoặc $B = 0$
$\left( {x - 3} \right).\left( {x + 2} \right) = 0$
\(\begin{array}{l}TH1:x - 3 = 0\\x = 0 + 3\\x = 3\left( {TM} \right)\end{array}\)
\(\begin{array}{l}TH2:x + 2 = 0\\x = 0 - 2\\x = - 2\left( L \right)\end{array}\)
Vậy có duy nhất \(1\) giá trị nguyên dương của \(x\) thỏa mãn là \(x = 3\)
Cho \(B = \left( { - 8} \right).25.{\left( { - 3} \right)^2}\) và \(C = \left( { - 30} \right).{\left( { - 2} \right)^3}.\left( {{5^3}} \right)\) . Chọn câu đúng.
-
A
\(3.B = 50.C\)
-
B
\(B.50 = C.\left( { - 3} \right)\)
-
C
\(B.60 = - C\)
-
D
\(C = - B\)
Đáp án của giáo viên lời giải hay : B
Thực hiện lũy thừa trước rồi nhân các số nguyên với nhau.
+ Muốn nhân hai số nguyên âm, ta nhân hai giá trị tuyệt đối của chúng
+ Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu (-) trước kết quả nhận được
\(B = \left( { - 8} \right).25.{\left( { - 3} \right)^2} = - 200.9 = - 1800\)
\(\begin{array}{l}C = \left( { - 30} \right).{\left( { - 2} \right)^3}.\left( {{5^3}} \right)\\ = \left( { - 30} \right).\left( { - 8} \right).125\\ = \left( { - 30} \right).\left( { - 1000} \right)\\ = 30000\end{array}\)
Khi đó \(B.50 = - 1800.50 = - 90000;\) \(C.\left( { - 3} \right) = 30000.\left( { - 3} \right) = - 90000\)
Vậy \(B.50 = C.\left( { - 3} \right)\)
Tìm \(x\) biết $2\left( {x - 5} \right) - 3\left( {x - 7} \right) = - 2.$
-
A
\(x = 13\)
-
B
\(x = 5\)
-
C
\(x = 7\)
-
D
\(x = 6\)
Đáp án của giáo viên lời giải hay : A
Bước 1: Áp dụng tính chất của phép nhân để phá ngoặc
Bước 2: Thu gọn vế trái
Bước 3: Tìm $x$
$\begin{array}{l}2\left( {x - 5} \right) - 3\left( {x - 7} \right) = - 2\\2x - 10 - 3.x + 3.7 = - 2\\2x - 10 - 3x + 21 = - 2\\\left( {2x - 3x} \right) + \left( {21 - 10} \right) = - 2\\\left( {2 - 3} \right)x + 11 = - 2\\ - x + 11 = - 2\\ - x = - 2 - 11\\ - x = - 13\\x = 13\end{array}$
Có bao nhiêu giá trị \(x\) thỏa mãn $\left( {x - 6} \right)\left( {{x^2} + 2} \right) = 0?$
-
A
\(0\)
-
B
\(2\)
-
C
\(3\)
-
D
\(1\)
Đáp án của giáo viên lời giải hay : D
Sử dụng kiến thức: $A.B = 0,B \ne 0 \Rightarrow A = 0$
Lưu ý: ${a^2} \ge 0$ với mọi $a$
$\left( {x - 6} \right)\left( {{x^2} + 2} \right) = 0$
Vì \({x^2} \ge 0\) với mọi \(x\) nên \({x^2} + 2 \ge 0 + 2 = 2\) hay \({x^2} + 2 > 0\) với mọi \(x\)
Suy ra
\(\begin{array}{l}x - 6 = 0\\x = 0 + 6\\x = 6\end{array}\)
Vậy chỉ có \(1\) giá trị của \(x\) thỏa mãn là \(x = 6\)
Cho \(A = \left( {135 - 35} \right).\left( { - 47} \right) + 53.\left( { - 48 - 52} \right)\) và \(B = 25.\left( {75 - 49} \right) + 75.\left| {25 - 49} \right|.\)
Chọn câu đúng.
-
A
\(A\) và \(B\) đối nhau
-
B
\(A\) và \(B\) bằng nhau
-
C
\(A\) và \(B\) cùng dấu
-
D
\(A\) và \(B\) trái dấu
Đáp án của giáo viên lời giải hay : D
+) Thực hiện phép tính trong ngoặc trước, đổi dấu hai thừa số, đặt thừa số chung rồi áp dụng quy tắc nhân hai số nguyên khác dấu.
+) Lập luận để phá dấu giá trị tuyệt đối, áp dụng tính chất phân phối để nhân phá ngoặc, nhóm các tích và đặt thừa số chung, sử dụng quy tắc nhân hai số nguyên cùng dấu.
\(\begin{array}{l}A = \left( {135 - 35} \right).\left( { - 47} \right) + 53.\left( { - 48 - 52} \right)\\ = 100.\left( { - 47} \right) + 53.\left( { - 100} \right)\\ = \left( { - 100} \right).47 + 53.\left( { - 100} \right)\\ = \left( { - 100} \right).\left( {47 + 53} \right)\\ = \left( { - 100} \right).100\\ = - 10000\end{array}\)
Vì \(25 - 49 < 0\) nên \(\left| {25 - 49} \right| = - \left( {25 - 49} \right) = 49 - 25\)
\(\begin{array}{l}B = 25.\left( {75 - 49} \right) + 75.\left| {25 - 49} \right|\\ = 25.\left( {75 - 49} \right) + 75.\left( {49 - 25} \right)\\ = 25.75 - 25.49 + 75.49 - 75.25\\ = \left( {25.75 - 75.25} \right) + \left( { - 25.49 + 75.49} \right)\\ = 0 + 49.\left( { - 25 + 75} \right)\\ = 49.50\\ = 2450\end{array}\)
Do đó \(A\) và \(B\) là hai số nguyên trái dấu.
Số cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(x.y = - 28\) là:
-
A
\(3\)
-
B
\(6\)
-
C
\(8\)
-
D
\(12\)
Đáp án của giáo viên lời giải hay : D
- Tìm bộ các số nguyên có tích bằng \( - 28\)
- Tìm \(x,y\) và kết luận.
Vì \( - 28 = - 1.28 = 1.\left( { - 28} \right)\)\( = - 2.14 = 2.\left( { - 14} \right)\)\( = - 4.7 = 4.\left( { - 7} \right)\)
Nên ta có các bộ \(\left( {x;y} \right)\) thỏa mãn bài toán là:
\(\left( { - 1;28} \right),\left( {28; - 1} \right),\)\(\left( {1; - 28} \right),\left( { - 28;1} \right),\)\(\left( { - 2;14} \right),\left( {14; - 2} \right),\)\(\left( {2; - 14} \right),\left( { - 14;2} \right),\)\(\left( { - 4;7} \right),\left( {7; - 4} \right),\)\(\left( {4; - 7} \right),\left( { - 7;4} \right).\)
Có tất cả \(12\) bộ số \(\left( {x;y} \right)\) thỏa mãn bài toán.
Giá trị nhỏ nhất của biểu thức $3{(x + 1)^2} + 7$ là
-
A
\(0\)
-
B
\(7\)
-
C
\(10\)
-
D
\( - 7\)
Đáp án của giáo viên lời giải hay : B
Sử dụng đánh giá:
+ Nếu \(c > 0\) thì \(c.{a^2} + b \ge b\)
+ Nếu \(c < 0\) thì \(c.{a^2} + b \le b\)
Ta có:
\({\left( {x + 1} \right)^2} \ge 0\) với mọi \(x\)
\( \Rightarrow 3.{\left( {x + 1} \right)^2} \ge 0\) với mọi \(x\)
\( \Rightarrow 3{\left( {x + 1} \right)^2} + 7 \ge 0 + 7\)
\( \Rightarrow 3{\left( {x + 1} \right)^2} + 7 \ge 7\)
Vậy GTNN của biểu thức là \(7\) đạt được khi $x=-1.$
Tính giá trị của biểu thức: $A = ax - ay + bx - by$ biết $a + b = - 5;x - y = - 2$
-
A
\(7\)
-
B
\(10\)
-
C
\( - 7\)
-
D
\( - 3\)
Đáp án của giáo viên lời giải hay : B
Bước 1: Thu gọn biểu thức $A$ về dạng xuất hiện $a + b,x - y$
Bước 2: Thay $a + b,x - y$ vào biểu thức vừa thu gọn để tính.
$A = ax - ay + bx - by$ $ = (ax - ay) + (bx - by)$ $ = a.(x - y) + b.(x - y)$ $ = (a + b).(x - y)$
Thay $a + b = - 5;x - y = - 2$ ta được:
\(A = \left( { - 5} \right).\left( { - 2} \right) = 10\)
Tìm \(x \in Z\) biết \(\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\).
-
A
\(90,6\)
-
B
Không có $x$ thỏa mãn.
-
C
\(50,5\)
-
D
\( - 50,5\)
Đáp án của giáo viên lời giải hay : B
- Sử dụng quy tắc bỏ ngoặc.
- Nhóm \(x\) lại với nhau, nhóm số tự nhiên vào một nhóm.
- Áp dụng công thức tổng các số cách đều nhau:
Số số hạng = (Số cuối - số đầu):khoảng cách +1
Tổng = (Số cuối + số dầu).số số hạng :2
\(\begin{array}{l}\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\\(x + x + .... + x) + (1 + 2 + ... + 100) = 0\\100{\rm{x}} + (100 + 1).100:2 = 0\\100{\rm{x}} + 5050 = 0\\100{\rm{x}} = - 5050\\x = - 50,5\end{array}\)
Mà \(x\in Z\) nên không có $x$ thỏa mãn.
Có bao nhiêu cặp số \(x;y \in Z\) thỏa mãn \(xy + 3x - 7y = 23?\)
-
A
\(1\)
-
B
\(2\)
-
C
\(3\)
-
D
\(4\)
Đáp án của giáo viên lời giải hay : D
Chuyển vế, nhóm các hạng tử để đưa về dạng \(X.Y=a\); \(a \) là số nguyên.
\(\begin{array}{l}xy + 3{\rm{x}} - 7y - 23 = 0\\xy + 3x - 7y - 21 - 2 = 0\\x(y + 3) - 7(y + 3) = 2\\(x - 7)(y + 3) = 2\end{array}\)
Ta có các trường hợp:

Vậy các cặp số \((x,y)\) là \(\left\{ {\left( {8; - 1} \right);\left( {9; - 2} \right);\left( {6; - 5} \right);\left( { - 5; - 4} \right)} \right\}\)
Vậy có 4 cặp số thỏa mãn bài toán.
Giá trị biểu thức: \(15x - 23\) với \(x = - 1\) là:
-
A
\( - 8\)
-
B
\( 8\)
-
C
\( 38\)
-
D
\( -38\)
Đáp án của giáo viên lời giải hay : D
Bước 1: Thay \(x=-1\) vào biểu thức
Bước 2: Thực hiện phép nhân hai số nguyên trái dấu
Bước 3: Thực hiện phép trừ.
Thay \(x = - 1\) vào biểu thức ta được:
\(15.\left( { - 1} \right) - 23 = \left( { - 15} \right) - 23 = \left( { - 15} \right) + \left( { - 23} \right) = - 38\)
Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là?
-
A
\(120\) triệu
-
B
\( - 120\) triệu
-
C
\(300\) triệu
-
D
\(40\) triệu
Đáp án của giáo viên lời giải hay : A
Một quý gồm 3 tháng.
Tính lợi nhuận quý II: Lấy lợi nhuận mỗi tháng quý này nhân với 3.
Lợi nhuận 6 tháng đầu năm bằng lợi nhuận quý I cộng lợi nhuận quý II.
* Lợi nhuận Quý I là \((- 30) . 3 = - 90\) triệu đồng.
* Lợi nhuận Quý II là \(70 . 3 = 210\) triệu đồng.
Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là: \((- 90) + 210 = 120\) triệu đồng.
Giá trị nào dưới đây của \(x\) thỏa mãn \( - 6\left( {x + 7} \right) = 96?\)
-
A
\(x = 95\)
-
B
\(x = - 16\)
-
C
\(x = - 23\)
-
D
\(x = 96\)
Đáp án của giáo viên lời giải hay : C
\(\begin{array}{l} - 6\left( {x + 7} \right) = 96\\x + 7 = 96:\left( { - 6} \right)\\x + 7 = - 16\\x = - 16 - 7\\x = - 23\end{array}\)
Có bao nhiêu cặp số \(\left( {x;y} \right)\) nguyên biết: \(\left( {x - 1} \right)\left( {y + 1} \right) = 3?\)
-
A
\(1\)
-
B
\(3\)
-
C
\(2\)
-
D
\(4\)
Đáp án của giáo viên lời giải hay : D
- Tìm các cặp số có tích bằng \(3\)
- Lập bảng tìm các giá trị của \(x,y\) và kết luận.
Ta có: \(3 = 1.3 = 3.1 = \left( { - 1} \right).\left( { - 3} \right) = \left( { - 3} \right).\left( { - 1} \right)\)
Ta có bảng:
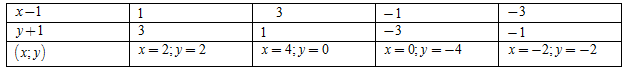
Vậy có \(4\) cặp số \(\left( {x;y} \right)\) thỏa mãn là: \(\left( {2;2} \right),\left( {4;0} \right),\left( {0; - 4} \right),\left( { - 2; - 2} \right)\)
Bạn Hồng đang ngồi trên máy bay, bạn ấy thấy màn hình thông báo nhiệt độ bên ngoài máy bay là \( - 28^\circ C\). Máy bay đang hạ cánh, nhiệt độ bên ngoài trung bình mỗi phút tăng lên \(4^\circ C\). Hỏi sau 10 phút nữa nhiệt độ bên ngoài máy bay là bao nhiêu độ C?
-
A
\({24^o}C\)
-
B
\( - {12^o}C\)
-
C
\( - {24^o}C\)
-
D
\({12^o}C\)
Đáp án của giáo viên lời giải hay : D
Nhiệt độ bên ngoài máy bay sau 10 phút bằng nhiệt độ ban đầu cộng với nhiệt độ tăng lên trong 10 phút đó.
Nhiệt độ bên ngoài sau 10 phút là \( - 28 + 10.4 = - 28 + 40 = 12^\circ C\)
