.jpg)
\(\dfrac{3}{5}\) là phân số. Đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác \(0\) viết dưới gạch ngang.
Do đó \(\dfrac{3}{5}\) là phân số.
.gif)
Trong các cách viết phân số sau, cách viết nào sai?
A. \(\dfrac{3}{8}\)
B. \(\dfrac{{12}}{1}\)
C. \(\dfrac{0}{{100}}\)
D. \(\dfrac{{35}}{0}\)
D. \(\dfrac{{35}}{0}\)
\(\dfrac{3}{8};\,\,\dfrac{{12}}{1};\,\,\dfrac{0}{{100}}\) là các phân số vì có mẫu số khác \(0\).
\(\dfrac{{35}}{0}\) không là phân số vì có mẫu số bằng \(0\).

Điền số thích hợp vào ô trống:
Tử số của phân số \(\dfrac{{17}}{{35}}\) là
Tử số của phân số \(\dfrac{{17}}{{35}}\) là
Trong một phân số, tử số là số tự nhiên viết trên dấu gạch ngang.
Trong một phân số, tử số là số tự nhiên viết trên dấu gạch ngang.
Tử số của phân số \(\dfrac{{17}}{{35}}\)là \(17\).
Vậy đáp án đúng điền vào ô trống là \(17\).

Điền số thích hợp vào ô trống:
Mẫu số của phân số \(\dfrac{{23}}{{50}}\) là
Mẫu số của phân số \(\dfrac{{23}}{{50}}\) là
Trong một phân số, mẫu số là số tự nhiên viết dưới dấu gạch ngang.
Trong một phân số, mẫu số là số tự nhiên viết dưới dấu gạch ngang.
Mẫu số của phân số \(\dfrac{{23}}{{50}}\) là \(50\).
Vậy đáp án đúng điền vào ô trống là \(50\).

Điền số thích hợp vào ô trống:
Phân số "Chín phần chín mươi mốt" được viết là:
Trong một phân số, tử số là số tự nhiên viết trên dấu gạch ngang, mẫu số viết dưới dấu gạch ngang.
Phân số: "Chín phần chín mươi mốt" được viết là \(\dfrac{9}{{91}}\).
Cho hình vẽ như sau:
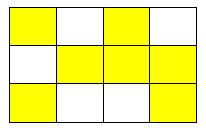
Phân số chỉ số ô vuông đã tô màu trong hình đã cho là:
A. \(\dfrac{5}{{12}}\)
B. \(\dfrac{7}{{12}}\)
C. \(\dfrac{5}{7}\)
D. \(\dfrac{7}{5}\)
B. \(\dfrac{7}{{12}}\)
Quan sát hình vẽ, tìm ô vuông được tô màu và tổng số ô vuông. Phân số chỉ số ô vuông đã tô màu có tử số là số ô vuông được tô màu và mẫu số là tổng số ô vuông.
Quan sát hình vẽ ta thấy có tất cả \(12\) ô vuông, trong đó có \(7\) ô vuông được tô màu. Vậy phân số chỉ số ô vuông đã tô màu trong hình là \(\dfrac{7}{{12}}\).

Người ta đã tô màu \(\dfrac{5}{9}\) số ngôi sao của hình nào dưới đây?



Quan sát hình vẽ và tìm phân số chỉ số ngôi sao được tô màu của mỗi hình.
Nhìn vào \(2\) hình trên ta thấy:
+ Hình \(1\) có tất cả \(8\) ngôi sao như nhau, trong đó có \(5\) ngôi sao được tô màu.
Vậy phân số chỉ số ngôi sao được tô màu của hình \(1\) là \(\dfrac{5}{8}\).
+ Hình \(2\) có tất cả \(9\) ngôi sao như nhau, trong đó có \(5\) ngôi sao được tô màu.
Vậy phân số chỉ số ngôi sao được tô màu của hình \(2\) là \(\dfrac{5}{9}\).
Như vậy, người ta đã tô màu \(\dfrac{5}{9}\) số ngôi sao của hình \(2\).
Cho hình vẽ như sau:
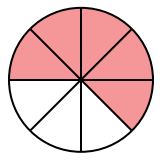
Quan sát hình vẽ, tìm số phần được tô màu và tổng số phần. Phân số chỉ phần tô màu trong hình có tử số là số phần được tô màu và mẫu số là tổng số phần.
Quan sát hình vẽ ta thấy hình tròn được chia thành \(8\) phần bằng nhau, trong đó có \(5\) phần được tô màu.
Vậy phân số chỉ số phần được tô màu là \(\dfrac{5}{8}\).
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(5\,;\,\,8\).

Phân số \(\dfrac{{18}}{{45}}\) được đọc là:
A. Mười tám phần bốn lăm
B. Mười tám phần bốn mươi năm
C. Một tám phần bốn năm
D. Mười tám phần bốn mươi lăm
D. Mười tám phần bốn mươi lăm
Đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.
Phân số \(\dfrac{{18}}{{45}}\) được đọc là mười tám phần bốn mươi lăm.

Điền số thích hợp vào ô trống:
Phân số có tử số là $63$, mẫu số là $197$ được viết là
Viết tử số trên gạch ngang rồi viết mẫu số dưới gạch ngang.
Phân số có tử số là $63$, mẫu số là $197$ được viết là \(\dfrac{{63}}{{197}}\).

Phân số nào dưới đây có tử số là \(24\) và mẫu số là \(55\)?
A. \(\dfrac{{24}}{{55}}\)
B. \(\dfrac{{55}}{{24}}\)
C. \(\dfrac{{55}}{{42}}\)
D. \(\dfrac{{42}}{{55}}\)
A. \(\dfrac{{24}}{{55}}\)
Trong một phân số, tử số là số tự nhiên viết trên dấu gạch ngang, mẫu số viết dưới dấu gạch ngang.
Phân số có tử số là \(24\) và mẫu số là \(55\) được viết là \(\dfrac{{24}}{{55}}\).

Phân số có tử số là số nhỏ nhất có hai chữ số giống nhau, mẫu số là số chẵn lớn nhất có hai chữ số được đọc là
A. Mười một phần chín mươi chín
B. Hai mươi hai phần chín mươi tám
C. Mười một phần chín mươi tám
D. Hai mươi hai phần chín mươi chín.
C. Mười một phần chín mươi tám
- Tìm số nhỏ nhất có hai chữ số giống nhau và số chẵn lớn nhất có hai chữ số rồi viết phân số đó. Viết tử số trên gạch ngang rồi viết mẫu số dưới gạch ngang.
- Đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.
Số nhỏ nhất có hai chữ số giống nhau là \(11\).
Số chẵn lớn nhất có hai chữ số là \(98\).
Phân số có tử số là số nhỏ nhất có hai chữ số giống nhau, mẫu số là số chẵn lớn nhất có hai chữ số được viết là \(\dfrac{{11}}{{98}}\).
Phân số \(\dfrac{{11}}{{98}}\) được đọc là mười một phần chín mươi tám.

Có thể viết được bao nhiêu phân số từ ba chữ số \(2\,;\,\,4\,;\,\,7\), trong đó tử số và mẫu số là các số có một chữ số và tử số khác mẫu số?
A. \(6\) số
B. \(7\) số
C. \(8\) số
D. \(9\) số
A. \(6\) số
Từ các số đã cho ta có thể viết được các phân số mà tử số khác mẫu số đó là:
\(\dfrac{2}{4}\,;\,\,\dfrac{4}{2}\,;\,\,\dfrac{2}{7}\,;\,\,\dfrac{7}{2}\,;\,\,\dfrac{4}{7}\,;\,\,\dfrac{7}{4}\)
Vậy có \(6\) phân số thoả mãn yêu cầu đề bài.

Mẹ mua về \(3\) chục quả trứng. Buổi sáng mẹ dùng \(\dfrac{1}{6}\) số trứng đó. Buổi trưa mẹ đã dùng \(8\) quả trứng . Vậy phân số chỉ số quả trứng còn lại là:
A. \(\dfrac{8}{{30}}\)
B. \(\dfrac{{13}}{{17}}\)
C. \(\dfrac{{17}}{{30}}\)
D. \(\dfrac{{13}}{{30}}\)
C. \(\dfrac{{17}}{{30}}\)
- Đổi \(3\) chục quả trứng $ = {\rm{ 3}}0$ quả trứng.
- Tìm số quả trứng mẹ dùng buổi sáng tức là ta tìm \(\dfrac{1}{6}\) của \(30\), hay ta lấy \(30\) chia cho \(6\).
- Tìm số trứng mẹ đã dùng trong cả hai buổi.
- Tìm số trứng còn lại ta lấy tổng số quả trứng trừ đi số trứng đã dùng.
- Viết phân số chỉ số quả trứng còn lại, tử số là số quả trứng còn lại, mẫu số là tổng số quả trứng ban đầu mẹ mua về.
Đổi : \(3\) chục quả trứng $ = {\rm{ 3}}0$ quả trứng.
Buổi sáng mẹ đã dùng số quả trứng là:
$30:6 = 5$ (quả trứng)
Số quả trứng mẹ đã dùng trong cả hai buổi là
$5 + 8 = 13$ (quả trứng)
Số quả trứng chưa dùng là:
$30 - 13 = 17$ (quả trứng)
Vậy phân số chỉ số quả trứng còn lại là: \(\dfrac{{17}}{{30}}\).
