Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
LG a
\(2x - 3 > 0\);
Phương pháp giải:
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
Lời giải chi tiết:
Ta có
\(\eqalign{& \,\,2x - 3 > 0 \cr & \Leftrightarrow 2x > 3 \cr & \Leftrightarrow x > 3:2\cr & \Leftrightarrow x > {3 \over 2} \cr} \)
Vậy nghiệm của bất phương trình là \(x > \dfrac{3}{2} \) và được biểu diễn trên trục số như sau:
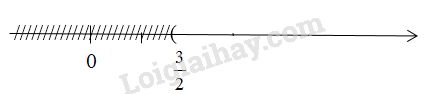
LG b
\(3x + 4 < 0\);
Phương pháp giải:
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
Lời giải chi tiết:
Ta có
\(\eqalign{
&\,\,3x + 4 < 0 \cr
& \Leftrightarrow 3x < - 4 \cr
& \Leftrightarrow x < {{ - 4} \over 3} \cr} \)
Vậy nghiệm của bất phương trình là \( x < \dfrac{{ - 4}}{3} \) và được biểu diễn trên trục số như sau:

LG c
\(4 - 3x ≤ 0\);
Phương pháp giải:
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
Lời giải chi tiết:
Ta có
\(\begin{array}{l}
4 - 3x \le 0\\
\Leftrightarrow 4 \le 3x\\
\Leftrightarrow \dfrac{4}{3} \le x
\end{array}\)
Vậy nghiệm của bất phương trình là \(x \geqslant \dfrac{4}{3}\) và được biểu diễn trên trục số như sau:
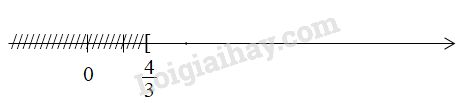
LG d
\(5 - 2x ≥ 0\).
Phương pháp giải:
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
Lời giải chi tiết:
Ta có
\(\begin{array}{l}
5 - 2x \ge 0\\
\Leftrightarrow 5 \ge 2x\\
\Leftrightarrow 2,5\ge x
\end{array}\)
Vậy nghiệm của bất phương trình là \( x \leqslant 2,5\) và được biểu diễn trên trục số như sau:

soanvan.me
