Đề bài
Dựng hình thang \(ABCD\; (AB // CD)\), biết \(AB = AD = 2\,cm,\) \( AC = DC = 4\,cm.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng phương pháp dựng tam giác, hình thang.
Lời giải chi tiết
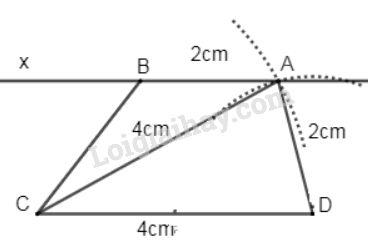
a) Phân tích
Giả sử dựng được hình thang \(ABCD\) thỏa mãn yêu cầu đề bài.
Tam giác \(ADC\) dựng được vì biết ba cạnh của tam giác.
Điểm \(B\) phải thỏa mãn hai điều kiện :
+ \(B\) nằm trên tia \(Ax\) song song với \(CD\)
+ \(B\) cách \(A\) một đoạn \(2\,cm.\)
b) Cách dựng
Dựng \(\Delta A{\rm{D}}C\):
- Vẽ đoạn thẳng \(CD = 4\,cm.\)
- Dựng cung tròn \((C; 4\,cm)\) và cung tròn \((D; 2\,cm)\), hai cung tròn này cắt nhau tại \(A.\)
- Nối \(A\) với \(C, A\) với \(D\) ta được \(\Delta A{\rm{D}}C\).
c) Chứng minh
Tứ giác \(ABCD\) là hình thang vì \(AB // CD\) (theo cách dựng).
Hình thang \(ABCD\) có \(AB = AD = 2\,cm\), \(AC = DC = 4\,cm\) thỏa mãn yêu cầu đề bài.
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn yêu cầu của đề bài.
