Đề bài
Dựng hình thang cân ABCD \(\left( {AB// CD} \right)\) biết AB = a, đường chéo AC = m, góc giữa hai đường chéo là \(\alpha .\)
Phương pháp giải - Xem chi tiết
+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.
+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.
+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài
Lời giải chi tiết
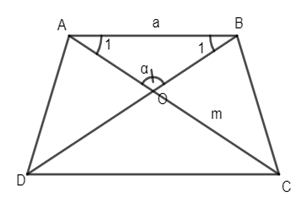
Phân tích: Giả sử hình thang cân ABCD đã dựng ta thấy tam giác cân AOB dựng được ngay biết \(AB = a,\widehat {AOB} = \alpha \)
\( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}} = \dfrac{{{{180}^ \circ } - \alpha } }{2} = {90^ \circ } -\dfrac{\alpha }{2}\)
Cần xác định hai đỉnh C và D.
+ D thuộc BO sao cho BD = m.
+ C thuộc tia AO sao cho AC = m.
Cách dựng:
- Dựng \(\Delta AOB\) biết AB = a, \(\widehat {OAB} = \widehat {OBA} = {90^ \circ } - \dfrac{\alpha }{2}.\)
- Lấy D thuộc tia BO sao cho BD = m.
- Lấy C thuộc tia AO sao cho AC = m.
Ta được hình thang ABCD cần dựng.
Chứng minh:
Theo cách dựng ta có tam giác OAB cân tại O có góc ở đáy là \(\widehat {OAB} = \widehat {OBA} = {90^ \circ } - \dfrac{\alpha }{2}\) nên \(\widehat {AOB} =\alpha\)
Vì AC=BD và OA=OB nên OD=OC. Suy ra tam giác ODC cân có góc ở đỉnh \(\widehat {COD}=\widehat {AOB} =\alpha\) (đối đỉnh) nên \(\widehat {ODC} = \widehat {OBA} = {90^ \circ } - \dfrac{\alpha }{2}\)
Mà hai góc \(\widehat {ODC} , \widehat {OBA} \) ở vị trí so le trong nên AB//CD. Suy ra ABCD là hình thang.
Có AB = a, đường chéo AC = m, góc giữa hai đường chéo là \(\widehat {AOB} =\alpha .\)
Vậy ABCD thỏa mãn đề bài.
Biện luận: Khi \(0 < \alpha < {180^ \circ }\) bài toán luôn có nghiệm hình.
soanvan.me
