Đề bài
Hình 105 minh họa: hình gồm một nửa hình cầu và một hình nón
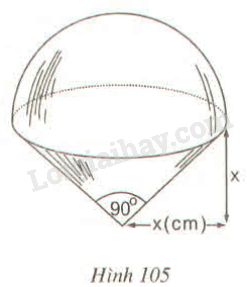
Thể tích của hình nhận giá trị nào trong các giá trị sau:
(A) \(\displaystyle {2 \over 3}\pi {x^3}(c{m^3})\) (B) \(\displaystyle \pi {x^3}(c{m^3})\)
(C) \(\displaystyle {4 \over 3}\pi {x^3}(c{m^3})\) (D) \(\displaystyle 2\pi {x^3}(c{m^3})\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Thể tích hình nón có bán kính đáy \(r\), chiều cao \(h\) là: \(V = \dfrac{1}{3}\pi {r^2}h\).
- Thể tích hình cầu bán kính \(r\) là: \(\displaystyle V ={4 \over 3}\pi {r^3}\).
Lời giải chi tiết
Hình gồm một nửa hình cầu có bán kính là \(x\) và một hình nón có bán kính đáy bằng \(x\), chiều cao bằng \(x\).
Thể tích nửa hình cầu là: \(\displaystyle {V_1} = {1 \over 2}.{4 \over 3}\pi {x^3} = {2 \over 3}\pi {x^3}(c{m^3})\)
Thể tích của hình nón là: \(\displaystyle {V_2} = {1 \over 3}\pi .{x^2}.x = {1 \over 3}\pi {x^3}(c{m^3})\)
Tổng thể tích của hai hình đó là: \(V=\displaystyle {2 \over 3}\pi {x^3} + {1 \over 3}\pi {x^3} = \pi {x^3}(c{m^3})\)
Chọn (B).
soanvan.me
