Đề bài
Một hình cầu đặt vừa khít vào bên trong một hình tựa như hình 108 (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng \(\displaystyle {2 \over 3}\) thể tích hình trụ.
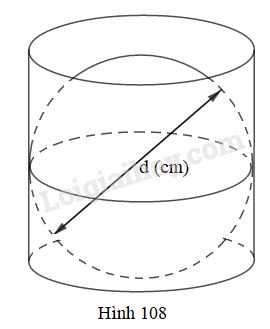
Nếu đường kính của hình cầu là \(d (cm)\) thì thể tích của hình trụ là:
(A) \(\displaystyle {1 \over 4}\pi {d^3}\left( {c{m^3}} \right)\) (B) \(\displaystyle {1 \over 3}\pi {d^3}\left( {c{m^3}} \right)\)
(C) \(\displaystyle {2 \over 3}\pi {d^3}\left( {c{m^3}} \right)\) (D) \(\displaystyle {3 \over 4}\pi {d^3}\left( {c{m^3}} \right)\)
Hãy chọn kết quả đúng.
Phương pháp giải - Xem chi tiết
Sử dụng: Thể tích hình trụ có bán kính đáy \(r\), chiều cao \(h\) là: \(V = \pi {r^2}h\).
Lời giải chi tiết
Ta có bán kính hình cầu bằng bán kính đáy hình trụ, chiều cao hình trụ bằng đường kính hình cầu.
Do đó, khi đường kính hình cầu là \(d (cm)\) thì bán kính đáy hình trụ là \(\dfrac{d}{2}(cm)\) và chiều cao hình trụ là \(d\) (cm).
Thể tích hình trụ là: \(\displaystyle V = \pi {r^2}.h = \pi .{\left( {{d \over 2}} \right)^2}.d = {1 \over 4}\pi {d^3}\) \(\left( {c{m^3}} \right)\)
Chọn (A).
soanvan.me
